Story of Mathematics	Category: SCI Published: 1993 #1607b
	Lloyd Motz et al.	16430u/18116r

Title	Story of Mathematics	数学物語
Index	Introduction Mathematics and mind: The origins of arithmetic: The origin of abstract matheatics: From geometry ot trigonometry Analytic geometry The birth of the calculus: Post-Newtonian mathematics: The golden age of mathematics: The end of the gloden age of Mathematics: The beginning of modern mathematics: Modern mathematics & the new physics: The evolution of modern mathematics: Whither mathematics?:	序文 数学と数学心: 算術の起源: 抽象数学の源流: 幾何から三角函数: 解析幾何学: 微分の誕生: ポスト･ニュートン数学: 数学黄金時代: 数学黄金時代の終わり: 近代数学の始まり: 近代数学と新たな物理学: 近代数学の進化: 数学はどこへ行くのか:
Tag	; Abel; Al-Khawrizmi; Apollonius; Archimedes; Aristarchus; Daniel Berunoulli; Jakob Bernoulli; Johann Bernoulli; Boole; Buffon; Cantor; Cardano; Cauchy; Cayley; Cramer; Dedekind; De Moivre; Descartes; Diophantus; Dirichlet; Einstein; Eratosthenes; Euclid ; Eudoxus; Fermat; Fourier; Frobenius; Galileo; Galois; Gauss; Hamilton; Hilbert; Hipparchus; I; Jacobi; Kepler; Kronecker; Kummer; Lagrange; Laplace; Leibnitz; Maclaurin; Mandelbrot; Maupertuis; Maxwell; Minkowski; Möbius; Napier; Neumann; O; Pascal; Pauli; Poincaré; Poisson; Ptolemy; Pythagoras; Q; Riemann; Russel; Rutherford; Schröndinger; Schewartzschild; Shannon; Snell; Taylor; Tartaglia; Thomson; Ulam; V; Weierstrass; X; Y; Z
	;

Résumé

Remarks

>Top 0. Introduction: In this story of mathematics, we trace the growth of mathematics from early Greeks (Pythagoras, Euclid, Archimedes, ...) to Newton and the great post-Newtonian mathematicians. >Top We note that Archimedes (c287-c282 BC) did not develop the calculus which Leibnitz and Newton did, some 2000 years later, even thought Archimedes was on the verge of doing so. The reason was that nothing in Archimedes's time demanded the calculus, whereas Newtonian science did. This is but one example of how societal, technological, and scientific needs shaped the development of mathematics, which, in turn revealed unsuspected scientific truths.

0. 序文: 古代ギリシャからニュートン、ポストニュートンの数学者までの歴史物語。 アルキメデスは、ライプニッツ=ニュートンが2000年後に行った微積分をその入口まで行ったがそれを発展させなかった。 アルキメデスの時代には微積分のニーズがなかった。 これは社会・技術・科学的なニーズと数学の発達との関連を示す。

>Top 1. Mathematics and Mind - Early Greeks and Alexandrians: All living creatures think; only humans generate abstract thought. the final result is different from the anticipated result. It is the only purely mental activity that can generate new concepts, having no relation to any aspect of the world. The universe is a rational entity, that correspond to every possible feature of the universe. Mathematics is the language, not the essence of science. Origins of mathematics; began in geometry; fully developed by the ancient Greeks. two of the may recreational activities; games and puzzles; then theory of games. life-supporting activities required mathematics; associated with animal husbandry, agriculture, commerce, shipping, and exploration. Flooding of the Nile signaled the beginning of the planting season; required some knowledge of angles and trigonometry. Shipping required precise knowledge of positions of the constellations from season to season, including various optical devices. these studies culminated many centuries later with inventions of camera, ,microscope, telescope, and spectroscope. Plane geometry: the first branch of mathematics fully developed by the ancient Greeks. >Top Euclid (Eukleides) of Alexandria (c330BC-c275BC) in his Elements used as a mathematical text for 1000 years. rigourous theoretical discipline based upon precise definitions, axioms, and theorems. 'Elements': the most famous and successful textbook of all time; there is no royal road to geometry. Importance of Euclid's works; transformed geometry from a purely utilitarian mental device to an abstract mental pursuit, governed by its own principles. involved such geometrical concepts as points, distances, directions, lines, surfaces (areas), and volumes. Point, the only undefinable element in Euclidean geometry. an infinite number of points lies between any two points Euclid introduced two other abstract concepts; definition and axiom. Axiom; are accepted as self-evident truths; form the foundation of a logical structure. the most famous axiom: given a straight line and a point outside this line, one and only one straight line can be drawn through the point parallel to the given line. Perfect number: the sum of its aliquot divisors equals the number itself.; 6, 28, 496, 8128, 3355036; no odd perfect numbers are known. God created all things in 6 days because this number is perfect. >Top Prime numbers: 1, 2, 3, 5, 7, 11, 13, 17, 19, ...; defined as one that has only 1 and itself as factors. Euclid proved that there is an infinite number of prime numbers reductio ad absurdum: the assumption that the theorem to be proved is false leads to an absurdity. $1×2×...×p+1$ must either¥ be a prime or divisible by a prime larger than Pythagoras (c569BC - c500BC): was a very charismatic and popular lecturer. number is everything.: the world is ruled by harmony; musical harmonies in terms of numeral ratios of the pitches. $c^2=b^2+b^2 \;(c: $hypotenuse >Top Eudoxus of Cnidus (c408BC-c355BC) astronomy and Medicine to geometry; description of constellations theory of the motions of planets, sun and moon. Aristarchus of Samos (c310BC -c230BC): the first to propose a heliocentric mode Eratosthenes of Cyrene (c276BC-c195BC): Sieve of Eratosthenes: ancient algorithm for finding all prime numbers up to any given limit. >Top Apollonius of Perge (260BC-200BC): defined fundamental conic property; parabola, ellipse, and hyperbola. >Top Archimedes (Claudius Ptolemaeus, 287BC-212BC), Syracuse: basic hydrostatic principle knew the irrational number $\pi$; the universe could not operate properly without the number $\pi$. designed huge catapults, large mirrors to set fire to Roman ships. "Eureka!" calculated $10^63$ grains of sand to fill the universe. Top 3 great mathematician in history: 1) Archimedes, 2) Newton, 3) Gauss >Top Hipparchus of Nicaea (c180BC-c125BC): calculated length of the year, inclination of the ecliptic to the equator, and the eccentricity of the solar orbit. ranked as the greatest of the Greek astronomers of the pre-Chirstian era. applied trigonometry to astronomical calculations. theory of epicycle: to account for the apparent motions of the planet. >Top Ptolemy, Alexandrian astronomer (c100AD-c170AD): two centuries of dearth of astronomical and mathematical activity, separating Hipparchus and Ptolemy. Romans were concerned with more earthly matters such as military conquest, commerce, construction, and the maintenance of a vast empire. Romans contributed little to mathematics. Current numeral system: goes back to the Hindus of 3C, BC. position of an integer in a many-digit number. Mathematics remained static for centuries even though Greek mathematics was accpted as a standard part of the curriculum in universities.

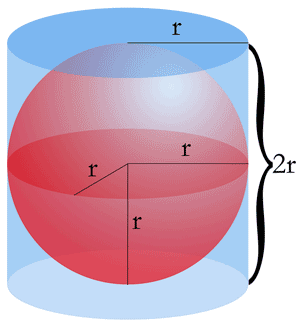
1. 数学と数学心 - 初期ギリシャとアレキサンドリア: 全ての生物は思考する。人間だけが抽象的思考をする。 ピタゴラス (534BC):   エウドクソス (381BC):       数学の起源: ユークリッド (302BC): 原論 平面幾何学     サモスのアリスタルコス (270BC):         アルキメデス (249BC)のEpitaph: Archimedes spher inscribed in a cylinder: Volume: $V_s=\frac{2}{3}V_c$ Surface area: $S_s=\frac{1}{4}S_c$ エラトステネス (235BC) ペルガのアポロニウス (230BC):   ヒッパルコス (152BC):     トレミー (プトレマイオス) (135BC):     記数法:

>Top 2. Origins of Arithmetic: Mathematics did not evolve sequentially and grew independently of each other; unlike physics. are all part of a vast intellectual fabric plane geometry: open-ended; developed without explicit reference to arithmetic or algebra. only with integers, soon expanded into fractions, irrational and complex numbers. became associated with order, organization, and information the rules of arithmetic can be applied not only to individual numbers but to collections of numbers or things (set theory) and infinitely large numbers (theory of transfinite numbers) not permitted to go outside these axioms in proving any theorems. Algebra: expanded far beyond its original domain. numbers were replaced by letters; numbers in disguise. algebraic entity is called a matrix or a mathematical operator which is used to transform one algebraic entity into another. some of the rules that govern numerical operations may be altered to introduce special branches of algebra. E.g.: the product of two algebraic entities depends on the order. has been applied to logic and language in a form called Boolean algebra. Elementary algebra: as a method of counting and keeping records of transactions. considered the relationship of Greek geometry to arithmetic. the symbol 0 for zero did not appear until a thousand years after the Babylonians first introduce written symbols for numbers. >Top Numbering system: In 3C BC: by the Hindus who used a straight line for one but adopted different symbols for quantities greater than one. In 8C AD: this numbering system was introduced to the Arabs, and first appeared in Europe in 976 AD; nine digits (1, 2, 3, ..., 9) were first used. ordering property as distict from its cardinal or quantitative property was introducced. The symbol 0 did not appear until a 1000 years after the Babylonians first introduced. The Maya first used 0 in the 1C AD; 500 years later it was adopted by the Hindus In 7C AD; the position of a digit in a many digit number was first used as a mark of the quantitative value of the digit. Four basic operations are defined; addition, subtraction, multiplication, and division Division: An important consequence of the division of one number by another is the concept of factors. Finding the factors of a number became one of the outstanding exercises in the theory o numbers; involving prime numbers and perfect numbers, both require knowledge of the factors of a number. Arab mathematicians about 900 AD: arithmeti symbolism began to appear in the arithmetic formulas, invlve raising a number to a power. The inverse operation of raising a power is finding the root of a number such as th square root. Importance of generalization: Generalizatons have been the most productive of all techniques in both mathematics and science. We cannot change apples and oranges to the same kind of entity but we can thirds and fifths to the same kind of mathematical entity; finding a common denominator, and reduced fraction. Decimal representation of a fraction; which stems from the ten-digit base of the nuber system; one of the greatest advances in the history of arithmetic. general rule for expressing any fraction as a decima, using decimal point. Fractions into two groups: nonrepeating decimal representation; irrationalnumbers. repeating decimal representations. Decimals also simplifid arithmetic opeartion in commerce, finance, and in scientific measurements. rates, as perentages, are also used in finance. 'Useless' mathematics: no practical use when it was first introduced but in time, let to the development of remarkable and beautiful branches of mathematics - the theory of functions of complex variables. without this apparently 'useless' mathematics, the development of mathematical features of the theory of relativity and the basic equations of quantum mechanics could not been discovered. The mathematics required to elucidate a particular phase of physics always preceded the conceptual discoveries of the physicist. the development or emergence of a certain branch of mathematics indicates the direction along which physics will ultimately evolve. >Top John Napier (1550-1617): defined the logarithm of a number; Johannes Kepler's calculations of the positions of the plant. produced the first of several table of logarithms; the base 10 was used. raising any nmber to some power and finding a root can be easily done with logarithms. Natural logarithm $e$:

2. 算術の起源: 算術はオープンエンド: 集合論 超限論 整数から分数、無理数、複素数へ 順序、組織、情報との関連し 集合論 無限数 (超越数) 代数学: 未知数を文字で 行列 一部規則の返納 内積 ブール函数   基礎代数: 数え上げ、取引記録 古典ギリシャ幾何との関係 0の表示 記数法: 3C BC: インド 7C: 桁表示 加減乗除 8C: アラブ 976: 欧州に登場 0表記には1000年かかった 割り算 素数･完全数 900: アラブの数学 平方根･立方根   一般化の重要性: 数学と科学にとって 小数点表示 商業･金融･科学に有効 10桁表示   数学のもしも: 最初は実用性なし この無用の数学なしには, 相対論や量子力学は誕生しなかった 数学での明晰性は物理概念の発見に先行 先に数学, その後物理   John Napier (1583): 対数を定義 ケプラーの天文計算に寄与 底数は10 その後自然対数$e$

>Top 3. The origin of abstract mathematics: >Top Algebra was the body of knowledge from which all other abstract mathematics emerged. Diophantus of Alexadria (c201-285 BC); father of Algebra Al-Khawrizmi (c780-c850): Arabic mathematician Al-Khawarizmi; algebra came from Arabic al-jabra (=reduction) Friar Luca Pacioli, 1447-1517; the first European (Renaissance) treatise on algebra. all the rules of arithmetic can be extended to symbols or letter; were introduced over a period of many years. multiplication sign × was generally dropped to avoid confusion; juxtaposition of two letters such as $xy$ the division sign was also eliminated and replaced by a slash (soldus) such as $x/y$ coefficient: like $3x$, or $x/3$, or $\frac{1}{3}x$ parentheses: product of one sum of terms and another sum of terms, like $(a+b+c)(x+y+z)$ minus sign: $-y$, or $-(a-b+c)$ expression to powers: $(x+y)^n$, or $(xyx)^n=x^ny^nz^n$ Modern algebra: even with the acceptance of these rules, modern algebra did not begin until late 18C and early 19C when Lagrange and Galois began to investigate the general solutions of algebraic equations. Scientific principles: many instances in science where relatively simple and elementary algebra was used to express important scientific principles; Newton's laws, etc. Polynomials, power and multiplied by some coefficient and variables; such as $a_nx^n$, where, $a_n$ is the numerical coefficient multiplying $x^n$ >Top function: one-to-one correspondence between the individual members of two different sets of quantities; $x=1, 2, 3, 4$, etc and another $y=2, 4, 6, 8$, etc; then we obtain $y=f(x)=2x$ all branches of science benefited greatly from the use of the function concept, which appears in every phase of physics literature. define the domain: the range of the function over which the function is defined. the function was later extended to entities different from numbers. algebraic equation; most fully developed branches of algebra in late 18C and early 19C. a solution of an algebraic equation is a numerical value of the unknown $x$ which makes the left-hand side of the equation 0.; also called a root of the equation. Leibnitz was the first to study the general function of $x$ or polynomials of the nth degree; he wrote as $f(x)=a_nx^n+z_{n-1}x^{n-1}+...+a_1x+a_0$ >Top Algebra of sets: the theory of sets, in its modern form, was created in 19C by German mathematician Georg Cantor 1845-1918); 'diagonal argument' The set in its most abstract form is a collection or aggregate of entities, all of which have similar properties that marke them specifically as belonging to the particular set in question. Linear and quadratic algebraic equations: were known to the Egyptians more than 4000 years ago. the general solution of the quadratic equation was probably known very early in the history of algebra: $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ in 16C Italian algebraists Niccolo Tartaglia (1499-1557) and Gerolamo Cardano (1501-1576) found the general formula for the three roots of the cubic equation express in terms of the coefficients. Gerolamo Cardano: Some years later, Italian Ludovico Ferrari (1522-1565) found a formula for a special case of the quartic equation. Polo Ruffini and later by Norwegian mathematician Niels Henrik Abel (1802-1829); proved that no formula higher than the fourth. >Top Algebra of matrices: owe a great debt to British Arthur Cayley (1821-1895) - and Sylvester, and Irish William Hamilton (1805-1865). not only in linear algebra and transformation theory but also in modern theoretical physics >Top 1854: Boolean algebra by British George Boole (1815-1864): sum and product, which are called union or logical sum of the sets, and intersection or logical product. forerunners of software language

3. 抽象数学の源流: 代数から全ての分野の抽象数学: ディオファントス (245BC), 代数の父 アラビアの数学者アル･フワリズミ (815) アルジェブラ < al-jabra ルカ･パチョーリ (1482): すべての算術の規則は文字記号 ×, /, -, ()の表記 近代代数学は18C末- 19C初に確立 ラグランジェ、ガロア   科学の原則: 科学現象は比較的簡潔。基礎代数で表記できる 多項式 函数: 1対1対応 函数概念は科学の全分野に役立つ 領域を定義 函数は数字から記号表示 代数式の発展 左式$x=$の表現 ライプニッツによる一般表現   集合論: 集合論の創設者 カントール (1881) 対角線論 線形･二次方程式: 4000年前にエジプトでは既知 16Cイタリア: タルタリア (1528)とカルダーノ(1538)による三次方程式の一般解 その数年後イタリアのルドヴィコ･フェラーリ(1543)が四次方程式の特定解 ポロ･ルフィーニ、その後アーベル (1815)は五次方程式以上の一般解はないことを証明 行列の代数: 英ケイリー (1858)とシルベスター、アイルランドのハミルトン (1835) 線形代数学、変換理論、近代理論物理 1854: ブール (1834): ブール函数 和は和集合または論理和$\cup$、 積は交わりまたは論理積$\cap$ ソフトウェア言語の先駆者

>Top 4. From Geometry to Trigonometry: Arithmetic is the main path because both geometry and algebra emerged from it. space in a mathematical sense has been extended from its primitive connotation of real space; to include fictitious space. Geometry could not have been developed without algebra. Trigonometry; grew out of the study of relationships of angles and distances. angle is not dimensional; is a pure number such as degrees and radians. one radian equals nearly 57.296 degree; an angle can be measured by measuring a length (arc of a circle), yet an angle is not a length. Using unit circle; three distances are introduced: $\sin\theta, \cos\theta, \tan\theta$ theorem of Pythagoras: $radius^2=\sin^2{\theta}+\cos^2{\theta}$ 1550BC: Egyptian papyrus; a relation correspond to cosine of an angle is mentioned; trigonometry probably originated in Egypt. Ancient Greek, until Hipparchus Ptolemy's famous Almagest around 0 AD: certainly known to Hindu and Arab; filled the gap in mathematics from the time of Ptolemy to European Renaissance. Algebra and Trigonometry: trigonometric functions differ from algebraic functions; trigonometry cannot be precisely expressed y algebraic polynomials. trigonometry are periodic functions and have the same value for an infinite number of values of $x$. finite polynomials have a finite number of roots but we may not conclude that every function that can be expressed as an infinite series has an infinite number of roots. $\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+ ...$; contains only odd number $\cos x=1-\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+ ...$; contains only even number we picture a real particle revolving along the circumference and imagine its shadows cast by appropriate beams of light on horizontal and vertical axes of the circle. out of phase; one shadow is moving toward the center of the circle the other is moving away from it. SHM (simple harmonic motion); important in physics. Trigonometric functions were first introduced to simplify the study of triangles; this subject arises in all kind of structural, architectural, navigational, surveying, and physical problems. >Top Trigonometric theorem: Sine theorem: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ First Cosine theorem: $a=b\cos C+c\cos B, ...$ Second Cosine theorem: $a^2=b^2+c^2-2bc\cos A, ...$ Positional astronomy; study of apparent positions and motions of stars and planet; celestial ecliptic and celestial equator spherical trigonometry; parallax of the nearest star; Alpha Centaur, 4.5 ly is $\frac{3}{4}$second of arc. 1725: Copernican theory had been fully accepted. >Top geometrical optics; light passes from one medium to another. important in the design of optical systems; camera lenses, telescopes, microscopes, TV, projector, optical fibers, eye glasses; Willebrod von Roijen Snell (Snellius, 1580-1626)'s law (16C); $\frac{\sin i}{\sin r}=\frac{c}{\nu}=n \;$(refraction of the glass) Jakob Bernoulli (1654-1705); Johann Bernoulli (1667-1748): l'Hôpital's rule Daniel Bernoulli (1700-1782): published hydrodinamica (Bernoulli's principle); friend of Euler Gabriel Cramer (1704-1752): Cramer's rule >Top Euler's equation by Leonhard Euler (1707-1783): Complex plane (by Gauss): real axis and imaginary axis. Every complex number must be related to the complex sum $\cos\theta+i\sin\theta$ 1748: Euler introduced number $e$。 Suppose annual interest is compounded continuously; at the end of one year your principal would more than double: $\lim_{n\to\infty}(1+\frac{1}{n})^n$ $e=1+1+\frac{1}{2}+\frac{1}{3!}+\frac{1}{4!}+ ...$ $e^{i\theta}=\cos\theta+i\sin\theta; \; e^{\frac{\pi i}{2}}=i; \;e^{\pi i}=-1; \; e^{2\pi i}=1$ It is difficult to understand how the infinite sum of $e$ described above raised to the power $2\pi i$ can possibly be 1. theory of functions of a complex variable; important to describe propagation of waves to behavior of electrons. Euler's interests broadened from astronomy, physics, medicine and theology. 1727: Euler taught medicine and physiology in St. Petersburg. his pencil seemed to surpass him in intelligence, so easily did his memoirs flow; published more than 500 books and papers during his lifetime. collection of all his mathematical works would fill three sets of encyclopedias; the most prolific mathematician in history. >Top De Moivre's theorem: Abraham de Moivre (1667-1754): $(\cos\theta+i\sin\theta)^n=\cos{n\theta}+i\sin{n\theta}$ $(\cos\theta+i\sin\theta)^2=\cos^2\theta-sin^2\theta+ 2i\sin\theta\cos\theta=\cos2\theta+i\sin2\theta$ $(\cos\theta+i\sin\theta)^3 \Rightarrow \cos3\theta=4\cos^3\theta-3\cos\theta; \; \sin3\theta=-4\sin^3\theta+3\sin\theta$ the binomial $(x+y)^n$ must be a sum of all products of powers of $x$ and $y$ with the sums of these powers adding up to $n$, and the sum of all numerical coefficients in this sum must equal $n$. De Moivre theorem says that the number of terms of the right hand side of the equation is always 2; but the magnitude of the angle, sine and cosine, is $n$ times the angle; this formula is useful in trigonometry. In spite of its simple and lowly origin, trigonometry plays an important simplifying role in all branches of mathematics and physics.

4. 幾何から三角函数: 算術から、幾何と代数が生まれた 空間概念 幾何は代数なしに発展しなかった 三角関数: 角度, ラジアン 単位円 古代ギリシャ; トレミー 0 AD: インドとアラブでは既知。トレミーからルネサンスの空白を埋める 代数と三角函数: 三角函数は代数函数とは異なる 三角函数は周期函数 有限の多項式は有限の根を持つ 無限数列は無限の根を持つとは言えない。 三角函数の例 単位円上の点の水平軸および垂直軸上への投影 位相の概念 単振動 三角函数: 星座の地図: 天の赤道、天の黄道(ecliptic) 球面三角法 幾何光学   L. オイラー (1745): 複素平面 $e$ の導入     ヤコブ･ベルヌーイ(1679): ヨハン･ベルヌーイ(1707): ダニエル･ベルヌーイ(1741): クラメール(1728):     ド･モアブル (1710)の定理:

>Top 5. Analytic Geometry - the geometrization of arithmetic and algebra: Three mathematicians - Descartes (1596-1650), Fermat (1601-1665), and Leibnitz (1646-1716); and three scientists - Galileo (1564-1642), Kepler (1571-1630), and Newton (1643-1727) whose theoretical discoveries greatly influenced and contributed to the convergence of various branches of mathematics into a single discipline; coordinate system to all functional relationships. The idea of expressing the orbits algebraically did not occur until Fermat in 1629, and Descartes in 1637; introduce their concepts of a coordinate system;by Kepler had already completed his arithmetic analysis of Tycho Brahe's data. Mathematical concepts evolve as pure thought with no immediately apparent relationship to the physical world. In time, these pure ideas acquire a concreteness and physical reality that transcends their mathematical roots. the importance of the use of graph to express experimental results is that it enables the experimental physicist to present his findings visually without reference to any preconceived mathematical formula. Kepler decided to work on the orbits of Mars, using Tycho Brahe's data. Isaac Newton was a master of all phases of mathematics known at the time and he used arithmetic, algebra, geometry, and trigonometry as needed, to demonstrate his won mathematical theorems and deductions in physics. >Top Newton's binomial theorem; which give the formula for the expansion of any power of the sum of two terms such as $(x+y)^n$ into a sum of individual products such as $x^3y^{n-3}$. In formulating his laws of motion and of gravity mathematically, Newton set the pattern of research for future scientists, establishing mathematical physics, later theoretical physics. >Top Descartes (1596-1650): seemed to believe that the dreams were haven-sent. Although the dreams continued a kaleidoscope of colorful images; to apply algebra to geometry and thereby use mathematics to unlock the secrets of the universe. the straight line $y=c+ax$ in the coordinate system, it must cut the $x$ axis (abscissa) at some point; 'root' by adding $bx^2$ to the function we can make it turn toward $x$ axis and cut it again (zero twice) if we add a term such as $dx^3$; three toots. the plotted curve of the function in the coordinates system wiggles up and down with respect to the $x$ axis, it creates hills 'maxima) and dales (minima). >Top Analytic geometry; the shape of the perimeter of a section obtained by cutting a right circular cone with a plane. all conic sections can be represented by the general quadratic equation in $x$ and $y$: $ax^2+by^2+cyx+dx+ey+f=0 \;$ where $a, b, c, d, e, f$ are real numbers. 'gedanken' (though) experiments: using only pencil and paper, the was the beginning of mathematical or theoretical physics. theoretical or mathematical physicists rarely thought of themselves as mathematicians even though they contributed significantly to the development of certain branches of mathematics. >Top Polar coordinate system (Gaussian coordinate system); the position of any point on the plane is given by the circle it ones on (distance of the origin) and the straight line it lies one (angle). this led to the most general way of representing geometry algebraically. Translation of coordinates; is written algebraically as $x'=x-h$ and $y'=y-k$ if we apply the operation (translation) $T$ to a coordinate system $S$, we obtain anther coordinate system $S'$. If $T_i$ is the identity transformation, then $T_iS=S$. The inverse translation is $S=T^{-1}S'$ and the product of two translations $T_1T_2$ is itself a translation; $T_1T_2=T_3$. A bast branch of mathematics has evolved from these simple rules.

5. 解析幾何学: 17Cまでに3人の数学者(デカルト)と3人の科学者 (ガリレオ1603、ケプラー1600、ニュートン1685) 座標概念の導入 数学概念の物理世界への応用 純粋が概念が物理的な現実を得て、数学的根拠を伝承 実験結果の表現にグラフの利用 ケプラーはティコ･ブラーエのデータを利用して火星軌道の計算。 ニュートンは当時知られていた算術・代数・幾何・三角函数を活用して、数学公式や物理的演繹を示した。 ニュートンの二項定理: 運動・重力を数学的に公式化。今後の科学研究のパターンを示した。 デカルト (1623): 代数の幾何への応用 直交座標 直線；根 二次曲線 $n$次曲線   解析幾何学: 円錐断面による二次曲線 思考実験 (gedanken) 極座標:   座標変換:

>Top 6. The birth of the Calculus The history of ideas: is replete with example of remarkable breakthroughs that have drastically altered the direction, methodology, and the conceptual basis of a discipline or a philosophy. Without the calculus, much of theoretical physics, chemistry, and astronomy would have never evolved. Calculus occurred almost simultaneously in theoretical physics and in pure mathematics. >Top Isaac Newton (1642-1727): initiated theoretical physics; the laws of motion and the law of gravity algebraically. Second law is important because it established the mathematical relationship between the motion of a body and the force acting on the body, which Aristotle and later Aristotelian physicists did not understand. the first step: separating fact from friction; introduced the concept of inertia into physics. Inertia is the property of a body (mass) which resists any change in the body's motion; After Galileo(1564-1642), Newton formulated his three laws of motion. >Top 1664: Bubonic plague, forcing the closing of Cambridge. In those two years, Newton made several most important mathematical discoveries; the binomial theorem, the calculus (he called 'fluxions'), and the law of universal gravitation. He also performed experiments with glass lenses; light is really a composite of many different colored bands of light. 1665 manuscript; one of the few pieces of evidence that Newton did on the calculus at Woolsthorpe. 1667, Newton returned to Cambridge, and was elected a fellow of Trinity College. Newton developed his corpuscular theory of light; built a reflecting telescope 1672; was elected to the Royal Society 1684 -86; developed almost all of his waking hours to work out; brought humanity's understanding of the universe from the darkness of ignorance; demonstrated how Kepler's laws could be derived from the law of gravitation. 1687; published 'Principia Mathematica'; even though Halley had generously paid the cost of the publication and reviewed all of the proofs. 1689; was selected to represent the university in Parliament. 1690; returned to Cambridge; seemed less interested in mathematics and science than ever before; was now nearly 50 years old and the science are supposed to be a young man's game. 1703: was elected president of the Royal Society. 1705: was knighted by Queen Anne, and became Sir Isaac Newton. Although Newton had retired from scient, the subsequent decade; embroiled in the famous controversy with Leibnitz over the discovery of the calculus. acknowledged his debt to his predecessors particularly Galileo and Kepler; "I seem to have been only like a boy, playing on the sea-shore, and diverting myself, in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me." 1716: when Leibnitz posed a problem that he fervently hoped would humble Newton. But Newton solved Leibnitz's problem in a few hours. 1727: died; was the most highly honored scientist of all time. Importance of mathematics to physics: Motion is governed by the law: $F=ma$ $Fd=mad \; $(where, $d$ is distance) $Fd$ is the work done on the body by the force $F$. the average speed is $\frac{v}{2}, so that $d=\frac{vt}{2}$ $Fd=\frac{1}{2}mv^2 \;$, which is called kinetic energy of the body. This is a statement of the principle of conservation of energy. >Top Leibnitz (1646-1716): 4 years after the birth of Newton 1677: completed the basic work on the calculus and published his results. the resulting controversy over whether English Newton or German Leibnitz had been the first to discover the calculus. Fortunately, history saw fit to split the difference; Newton was recognized as the first to develop the calculus while Leibnitz was acknowledged to have developed the superior notation. Libnitz's philosophical speculations; the entire universe consists of monads (discrete individual entities) Leibnitz's idea: if $x$ increases or decreases by infinitesimal amount $dx$, then $f(x)$ becomes $f(x+dx) and the change in $f(x)$ is $f(x+dx)-f(x)=dy$ the important quantity is not the total change, but the rate of change is $\frac{f(x+dx)-f(x)}{dx}=\frac{dy}{dx }$ deuced general rules for finding derivatives of functions; such as sine, cosine, and exponential. The is probably the single greatest intellectual tool ever devised; science and technology could not have grown rapidly without the calculus. >Top Differential calculus: application of calculus to the development of physics called statistical mechanics; the distributions with the maximum probabilities then determine physical state of the system. it altered entirely evolution of geometry, leading geometers to what is now called differential geometry. until the discovery of calculus, geometers dealt only with Euclidean geometry; geometry of curved surfaces such as spherical surfaces was not developed independently. Differential geometry: 19C mathematicians broke the curved surface down into infinitesimal domains; which could vary from domain from domain, was introduced. It was quickly extended to surfaces of any number of dimensions. infinite series: the function represented by a sum of higher derivatives, each multiplied by a different power of $x$; by sums of an infinite number of terms which is useful outgrowths of the differential calculus. >Top differential equations: are the language of scientists who can relate two or more widely differing branches of science; such as atomic theory, optics, astronomy, cosmology, and biology $\frac{dy}{dx}=f(x) \; \Rightarrow dy=f(x)dx$ infinitesimal amount $dy$ by which $y$ changes if the dependent variable $x$ changes by the infinitesimal amount $dx$. the differential equation enables us to trace the function $y$ from point to point; it breaks up the function into an infinitude of infinitesimal bits, which, when added together, give the function $y$ which is the solution of the differential equation. differential equations describe infinitesimal relationships among interdependent entities, they are ideally suited to the needs of the physicist who expresses the laws of nature in terms of infinitessimals. >Top Partial derivative: $F(x, y, z)$ depends on three spatial coordinates of a particle. If $x$ alone changes, the $F$ changes only with respect to the changes in $x$: $\frac{dF}{dx}$. If the particle is moving randomly so that $x$, $y$, and $z$ are all changing simultaneously, then the infinitesimal changes; $dF=(\frac{dF}{dx})(dx)+(\frac{dF}{dy})(dy)+(\frac{dF}{dz})(dz)$ this analysis led to partial differential equations. Brook Taylor (1685-1731) and Colin Maclaurin (1698-1746): Taylor theorem and Taylor series; $\displaystyle\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$ Maclaurin series: $\displaystyle\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$

6. 微分の誕生: アイデアの歴史:   アイザック･ニュートン (1684) 理論物理の創設 運動の第二法則 万有引力の法則 1642: 生まれ 様々な発見 1665発見 輝かしい経歴: 1664: 腺ペスト流行 1672: 王立協会員に 1687: プリンキピア発行 1703: 王立協会会長                       ライプニッツ (1681): 1677: 微分に関する出版 ニュートンとの先陣争い。 ライプニッツの優れた微分記法         微分: 微分幾何学     微分方程式: 科学における言語       偏微分:

>Top 7. Post-Newtonian Mathematics: Post-Newtonian mathematics was dominated by Euler (1707-1783) and Lagrange (1736-1813): Golden age of mathematics Euler: contributed primarily in pure mathematics (mathematical physics, or now theoretical physics). Joseph Louis Lagrange: contributed as much to mathematical physics. Lagrange clarified the energy concept in the form of partial differential equations; used to describe the motions of groups of particles and force fields as well as the motion of a single particle. >Top Euler and Lagrange showed independently that the corret path is given as the solution of a second-order partial differential equation, Euler-lagrange equation. Euler and Lagrange knew nothing about the teory of relativity or the quantum theory; their work in mathematical dynamics are of fundamental importance in both of these ramarkable physical theories. Euler: a pure mathematician; devoted most of his time to exploring algebra, algebraic eqautions, and analytic geometry; the study of infinite series. >Top French Maupertuis (1698-1759): the principle of least action: a freely moving particle chooses that path connecting two points along which its action is a minimum. $n$ body problem: Given $n$ gravitationally interacting bodies with arbitrary masses and volcitis distributed randomly throughout space, find the mathematical expressions for the orbits oft these bodies. Newton's law of motion and gravity permit one to write down one equation of motion for each body so that the problem entails solving $n$ simultaneous partial differential equations involving the time and spacital coordinates of all the bodies; $3n+1$ variables Lagrangian points: discovered the equilateral triangle three-body solution, poited out that the vertices of such a triangle are points of stability of the three-body system. the solar ystem consisting only two massive bodies (the sun and Jupiter), the motions of the other planets are hightly stable. >Top Pierre Simon de Laplace (1749-1827): showed the mean distances of the planets from the sun. nebular hypothes; the solar system evolved from a condensing clous of gaes. 1785: full membe of the French Acamedy of Sciences. used matehmatics to attack problems relating to the dynamics of the universe itself, while Lagrange mostly confined himself to abstract mathmatic questions. $\frac{2GM}{R}=c^2$ the concept of the black hole whose detailed properties can be deduced only from Einstein's general theory of relativity. Blaise Pascal (1623-1662): described 'Pensées' corresponded frequently with Fermat on the subjects of anlytic geometry and physics.

7. ポスト･ニュートン数学: モーペルテュイ (1728): 最小作用の原理 ラグランジェ (1774)     n-体問題:           ラプラス (1788):       パスカル (1642):

>Top 8. The Golden Age of Mathematics: Post-Newtonian era of mathematics: dominated by three great mathematicians: Euler, Lagrange, and Laplace. 18C had been characterized by the efforts of many mathematicians to consolidate and apply the calculus to a variety of problems. 19C, by contract, was marked by the growth of a new mathematics freedom which broke all the constraints that had tied mathematics to physics. 19C also marked a shift of the center of mathematics from France eastward to Germany; German mathematicians, spearheaded by Gauss, began to challenge this French leadership. Though Newtonian era had been dominated by English mathematicians, they had allowed their leading role to slip away from them during the post-Newtonian period primarily because Newton's influence was so great that the English academic community considered it sacrilegious to alter or extend Newtonian mathematical concept. indeed, any movement to adopt the Leibnitz notation $d$ for the derivative, as in $\frac{dy}{dx}$, rather than the Newtonian dot, as in $\dot{y}$, was severely criticized. >Top Évariste Galois (1811-1832): Considering the brilliance of his mathematical discoveries before 20 years old, we can only wonder in awe at what he might have accomplished had he lived a full life. Galois, greatly influenced by algebraic discoveries of Lagrange, completed Lagrange's unfinished work on the solution of algebraic equations. In the process, he founded the theory of groups with important applications to mathematics, physics, chemistry, and astronomy. 1828: Galois met the mathematician Louis-Paul-Émile Richard, who was better known for his ability to teach advanced mathematics than for his own mathematical research. In Galois, Richard saw a mathematician who cloud become the Gauss of France. Indeed, Galois might have fulfilled this promise had he lived long enough. 1829: he had put off submitting a paper summarizing his original work. He composed a paper summarizing his results and submitted it to the Academy of Sciences in the hopes of winning the coveted Grand Prize in Mathematics. But the black cloud over Galois appeared once again and the paper was lost by the Academy's secretary. His own revolutionary sentiments fueled by the proud boasts of his fellow revolutionaries a a Guard banquet, Galois was goaded into offering a toast to King Louis Philippe, which was interpreted by loyalists as a threat against the ruler's life; Galois was thrown into prison; the end result was a not-guilty verdict. Cauchy promptly lost the paper of Galois - the one that Jacobi called the most important mathematical discovery of the century and which Hermite declared had given future mathematicians 500 years of work -amidst the clutter of his own office. Group concept: Three simple rues define the group concept: Multiplication of any two of these elements give another element of the set. the set contains the identity - an element that leaves unchanged any element of the set it multiplies; the set contains the inverse of every element in the set so that an element multiplied by its inverse gives the identity. Let permutation $P_12$ be the interchange of the number 1 and 2: $P_12(1234)=2134; \; P_24(2134)=4132; \; P_24P_12(1234)=4132=P124$ the identity $IP=P$; and inverse permutation $P^{-1}P=I$ the product $P_1P_2\neq P_2P_1$; groups are noncommutative. Abel and Galois are both recognized today as the founders of group theory. Galois applied his theory of groups to show that no algebraic equation of a higher degree than 5 can be solved algebraically. Study of infinite series: whether converge (finite) or diverge (infinite): The harmonic series is: $1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}+...$ $=(1+\frac{1}{2})+(\frac{1}{3}+\frac{1}{4})+...+ (\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8})+...$, and then compare each group in parentheses with the groups in parentheses in the infinite series $>(\frac{1}{2}+\frac{1}{2})+(\frac{1}{4}+\frac{1}{4})+...+ (\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8})+... $ diverges (infinite). Thus, the series $1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+... $ diverges, because $\frac{1}{\sqrt{n}} >\frac{1}{n}$ Even if the comparison test does not show that the series diverges, we may not conclude that the series converges. Main trend of early 19C mathematics: emphasized the contributions of Galois and Abel. theory of numbers, probability theory geometry differential equations, differential geometry, calculus of variations and mathematical physics expanded rapidly during that ear. Theory of numbers and that of probability have one thing in common; they did not evolve as mainstream of mathematics: Theory of number: is considered as the purest branch of mathematics. Theory of probability: owing to its usefulness in prediction occurrence of natural events and in calculating the chance of winning at gambling. Gauss meant that theorems in number theory are easy to set up but exceedingly difficult to prove: The quantity $1×2×3×...×(n-1)+1$ is always divisible by $n$ if $n$ is a prime but never when $n$ has factors/ Every prime number of the from $4x+1$ can be expressed as the sum of two integers in one and only one way. Every even number can be expressed as the sum of two primes. The expression $2^x-1$ is a prime for a general formula for $x$. The equation $x^n+y^n=z^n$ does not hold for integer values of $x, y, z$ if the integer $n$ is larger than 2 (Fermat's last theorem) A month's intelligent instruction in the theory of numbers ought to be twice as instructive, twice as useful, and at least ten times as entertaining as the same amount of calculus for engineers. Gauss introduced 'congruence relation': 33=2×13+7; 33 is congruent to 7 modulo 13, or $33\equiv (mod 13)$ A congruence cannot be treated as an operation but it is governed by certain arithmetic and algebraic rules that are similar to those that govern ordinary algebraic equations. A congruence may add or subtract two congruences with the same modules: $33=7 (mod 13) and 35=9 (mod13)$ may be summed to give the congruence 68=16 (mod 13) A congruence may be multiplied by a common factor: 33×3=7×3 (mod 13)=21 (mod 13) Gauss demonstrated, congruences are very powerful analytical tools that enable one to determine the factors fairly large number and thus whether or not such numbers are primes. this is one of the most challenging problems in the theory of numbers. Theory of probability: Jakob Bernoulli after 1687: study of combinations number of permutations of $n$ things taken $p$ at a time. De Moivre; de Moivre first devoted probability and the laws of chance; de Moivre's theorem; $(\cos\theta+i\sin\theta)^n=\cos {n\theta}+i\sin{n\theta}$ Leibnitz suggested that a comprehensive and systematic treatise on games should be written and should consist of three parts: those games that depends on numbers alone; those games like chess that depend on position; those games like billiards that depend on motion. Buffon needle problem: 18C French naturalist Comte Geroges de Buffon (1707-1788) proposed. Given a smooth table on whose surface equidistant parallel lines is ruled, with $d$ the separation between any two neighboring line, what is the probability that a needle of length $L$ less than $d$ will intersect one of the lines if the needle is thrown randomly onto the table?; the probability is \frac{2L}{\pi d} this expression leads to an experimental way of determining the value of $\pi$ by merely counting the frequency with which the needle cuts one of the lines.

8. 数学の黄金時代: 数学のポスト･ニュートン時代 偉大な3人の数学者 オイラー、ラグランジェ、ラプラス 微分の発見はニュートンが先行したが、その優れた記法はライプニッツが発明   ガロア (1821): 群論 1828: 数学者ルイス･リチャードと会い、高等数学研究 人生を長がらえば、フランスのガウスになれた。 数学大賞への応募書類を科学アカデミーの秘書が紛失。 さらにコーシーがガロアの論文を受領後事務所内で紛失。 ジャコビ曰く今世紀の最重要の発見で、将来の数学者の500年分の業績に匹敵すると評価した論文であった。   群理論: 3原則 ２つの要素の積はその集合のもう一つの要素を与える。 集合には単位元が存在し、それを掛けても要素は変化しない。 集合には逆元が存在し、元とその逆元との積は単位元となる。 積は可換ではない。               無限級数:         合同関係:             確率理論:   ビュフォン(1747) の針

>Top 9. The End of the Golden Age of Mathematics: less attention to mathematical chronology; because mathematics did not grow linearly but branched out in many direction like a tree. Euler and Lagrange were clearly the dominant post-Newtonian mathematicians. Laplace was not so much an innovator in mathematics as he was an applier. Abel and Galois laid the foundation of golden age of mathematics: Abel: summations of infinite series and criteria for their convergence; later became the theory of functions or, more generally, mathematical analysis. Able also contributed to the theory of groups known as 'Abelian groups. Final phase of the golden age of mathematics was dominated by French mathematicians. But English and German mathematicians were beginning to challenge this French dominance. British mathematicians; Arthur Cayley, James Sylvester, and George Salmon. Irish William Rowan Hamilton William Kindon Clifford and George Green German Karl Friedrich Gauss (1777-1855), the greatest mathematician of all time; particularly in the realms of geometry and analysis. Karl Gustav Jakob Jacobi, Peter Lejeune Dirichlet, and Georg Friedrich Bernhard Riemann Cauchy or Euler Weierstrass, Kronecker, Dedekind, Cantor, Steiner, Kummer, Frobenius, and Möbius Gauss was simple man with simple needs; Gauss also continued to acquire new languages throughout his years, mastering most of the languages of Europe, including Russian and Sanskrit. Gauss's work pervades the entire field of mathematics; Augustin Louis Cauchy (1789-1857): the most versatile French mathematician of that year; a child of the French Revolution, a month after a Paris mob had stormed the Bastille. Cauchy's greatest contributions to mathematics were in the theory of functions of complex variables and to the criteria for the convergence of infinite series. But Cauchy promptly lost the paper of Galois (the most important mathematical discoveery of the century called by Jacobi). Jean Baptiste Joseph Fourier (1768-1830): Fourier series: le to another important concept; $\frac{a_0}{2}+\displaystyle\sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx})$ $a_n=\frac{1}{\pi}\displaystyle\int_{0}^{2\pi}f(x)\cos{nx}dx$ $b_n=\frac{1}{\pi}\displaystyle\int_{0}^{2\pi}f(x)\sin{nx}dx$ Expansion of theory: In considering the motion of a particle, we may describe this motion in a spatial frame of reference - in 3D Cartesian coordinate system $x, y, z$. Development of electricity and magnetism strengthened the concept to the force field so that mathematics had to be expanded to represent the properties of fields, particularly electromagnetic fields. Introduction of molecules are the basic constituents of gases led to the kinetic theory and statistical mechanics of gases, which necessitated the expansion of probability theory into the kind of mathematics. Ampere (electromagnetic), Malus (polarization of light), Fresnel (Huygens's wave theory of light, and Sadi Carnot (heat engine). German began to challenge France's intellectual leadership. Non-Euclidean geometry: Hyperbolic geometry; Russian Lobachevski and Hungarian Bolyai Elliptical geometry; by Riemann Parallel axiom (fifth axiom) of Euclidean geometry; Given a straight line and a point outside this line, one and only one straightline in the plane (determined by the given line and point) can be drawn through the point parallel to the given line. Gauss convinced that the parallel axiom is indeed an axiom and cannot be proved. Gauss proposed that the three angles of a triangle, formed by three lines connecting three different stars, be measured to see if their sum is 180º as demanded by Euclidean geometry; it underscores Gauss's rejection of any a priori concept about the correct geometry of space. Georg Friedrich Bernhard Riemann (1826-1866): a son of a pastor, born in Breselenz, Hanover, Germany. Georg and his five brothers & sisters all suffered from malnourishment and poor health. One of Georg's earliest interests, the theory of numbers; benefited greatly fro classic works of Gauss, Abel, and Cauchy. Riemann submitted his doctoral dissertation to the legendary Gauss for his review. 1857: was appointed assistant professor at Göttingen University. clarified extremely important discoveries including: elliptical modular function convergence of trigonometric series foundations of mathematical analysis precise definition of the integral concept Gauss and Riemann were the best of mid-19C German mathematicians; Second tier group including: Johann Peter Gustav Dirichlet (1805-1859), Karl Jacobi, Leopold Kronecker, Richard Dedekind, Hermann Grossmann, August Möbius, Karl Weierstrass, and Georg Cantor (founder of mathematics of transfinite numbers) August Ferdinando Möbius (1790-1868); famous for the Möbius strip Noncontinental mathematicians: Irish William Rowan Hamilton (1805-1865); worked in conjunction with Karl Gustav Jacob Jacobi (1804-1851); Hamilton-Jabobi equation mastered a dozen language; mastered Latin, Greek, Arabic, Sanskrit, and Hebrew by ten years old. Hamilton's mathematics would prove to be helpful to physicists such as Erwin Schorödinger in a wave theory of the quantum mechanics in 1920s. Hamilton's study of optics and dynamics may have marked the pinnacle of his career. Vector analysis (or Vector calculus): differentiation and integration of vector fields, primarily in 3D Euclidean space $\mathbb{R}^3$ originated some years before Riemann's geometrical theories. led to the development of the theory of transformations of coordinate systems. Arthur Caylay and James Joseph Sylvester. British physicist James Clerk Maxwell (1831-1879); electromagnetic theory of light. during the last quarter of 19C, thermodynamics; led important concept of entropy. Algebra of matrices is noncommutative; the product $T_2T_1$ is different from the the product $T_1T_2$. Matices are very important in the quantum mechanics of atomic structure. French Siméon Denis Poisson (1781-1840): introduced the concept of gravitational field potential; shad shown that the potential obeys a second-order partial differential equation. solution of this equation for any given distribution of masses gives the gravitational potential at all points of space.

9. 数学黄金時代の終わり: 数学は年代毎に行かない。 オイラーとラグランジェ アーベルとガロア   数学黄金時代: 仏が先行。英独が挑む ガウス (1816)の偉業 コーシー (1823):     フーリエ (1799)級数         非ユークリッド幾何学:                 リーマン (1846): ガウスとリーマン 19C半ば独数学者の中の偉業             ディリクレ (1832):   メルビウス (1829):   ハミルトン (1833) ヤコビ (1827)       マックスウェル (1855):   ポアソン (1810):

>Top10. The Beginning of Modern Mathematics: Thermodynamics: most universal and self-sufficient branch of physics. 1st law: conservation of energy $dQ=dU+dW$, where, work $W$, heat $Q$, and $internal gas energy $U$, this states that energy may appear in different forms but whatever its form, the total amount must remain the same. 2nd law: introduces the concept of entropy; $\frac{dQ}{T}=\frac{U}{T}+\frac{W}{T}$, where $\frac{dQ}{T}$ equals the differential $dS$ of the 1uantity $S$, the entropy. Entopy can never decrease regardless of what happens to the system being studies;d;l; equation of state of the gas: $\frac{PV}{T}=$ constant. heat and energy were known entities before Newton's time but no one understood how to relate heat to energy mathematically. Once this relationship was uncovered, a whole new branch of physics was revealed. last half of 19C: Earnst Kummer (1810-1893): Karl Theodor Wilhelm Weierstrass (1815-1897): Leopold Kronecker (1823-1891): Julius Wilhelm Richard Dedekind (1831-1916): Georg Ferdinand Frobenius (1849-1917): Georg Ferdinand Ludwig Philipp Cantor (1845-1918): one of the most misunderstood and revolutionary thinkers; was born in St. Petersburg. All the integers and fractions are denumerable, so that their set is assigned the transfinite cardinal number $\aleph_0$ The irrational numbers, however, cannot be counted and so the set of all irrational numbers has the transfinite cardinal number $\aleph_1,$ which is larger than $\aleph_0$. If we remove the infinite set of all even integers (transfinite cardinal number $\aleph_0$), we are still left with an infinite set of transfinite number: $\aleph_0+\aleph_0=\aleph_0$ and $\aleph_0-\aleph_0=\aleph_0$; the product of $\aleph_0$ and $\aleph_0$ is still $\aleph_0$. The same is true if we raise aleph zero to any power; we still get aleph zero.

10. 近代数学の始まり: 熱力学 熱力学第一法則 熱力学第二法則 エントロピー       クンマー (1851) ワイエルシュトラウス (1856) クロネッカー (1857) カントール (1881): 革命的思索者

>Top 11. Modern Mathematics and the New Physics: Most fundamental change in mathematics: occurred in mid-19C with introduction of non-Euclidean geometry. it altered our basic concepts of space, time, motion, energy, and continuity of physical processes; i erased the sharp division between particle and wave. mathematics of macroscopic systems such as the universe itself was also affected by the revolution in physics. Maxwell's electromagnetic equations: had to be amended to account for the non-radiating behavior of an electron when in an atom, her it behaves as though it were stationary. Matrix mechanics vs. wave mechanics: Newton's law of 'matrix mechanics' describing position and momentum of an electron using two sets of different matrices. Erwin Schrödinger (1887-1961) introduced a 'wave equation' for the electron to account for its motion in an atom. Paul Adrien Maurice Dirac (1902-1984): matrix mechanics and wave mechanics are completly equivalent. general mathematical discipline called quantum mechanics; physical entities are represented by noncommutative algebraic operators. a physically indivisible particle of matter (like an electron), or physically indivisible particle of energy (like a photon) can simultaneously be moving along two different spatially separate paths and then, at the will of the observer, reappear instantaneously as a single particle again. (must be an oxymoron) David Hilbert (1862-1943) developed a special kind of vector geometry of functions (infinite dimensional space) called Hilbert space, which geometrized the quantum mechanics. John von Neumann (1903-1957): carried out a complete theoretical analysis of the foundations tenets of quantum mechanics; The mathematical Foundations of Quantum Mechanics. Albert Einstein (1879-1955): the impact of non-Euclidean geometry on physics; special theory of relativity to general theory of relativity. "principle of equivalence" as first observed by Galileo. Since the general theory of relativity in 1915; tensor analysis had been fully developed. the curvature of space-time cannot be perceived from a physical point of view because the physical perception of curving is that of distorting a structure into a higher dimension. Curving 4D space-time makes no physical sense to us. we cannot conceive of 5D or 6D space in which to curve our 4D space-time. Theory of relativity greatly stimulated the development of new areas of mathematics: Henri Poincaré (1854-1912): from the group theoretic point of view; Einstein-Lorentz transformation; describing the theory as a natural 4D extension of Galilean-Newtonian 3D description of the universe. Hermann Minkowski (1864-1909): from the geometric aspect of relativity, describing 4D geometry. had been Einstein's teacher at Zurich University. to merge space and time into a 4D space-time manifold, Minkowski first multiplied the time $t$ by a speed to change it into a distance; $ct \; c$ is the speed of light. then Miskowski decided to multiply $i$ (imaginary unit) and defining $ict$ as the fourth dimension; Minkowski space of special relativity in relative theory, leads to the equation: if $E$ is the energy of the particle and $p$ is its momentum, the algebraic formula is $E^2=c^2p^2+m_0^2c^4$ $E=\pm\sqrt{c^2p^2+m_0^2c^4}$ at first sight it seems ridiculous because we cannot see how a particle can have negative kinetic energy. but in 1930, Paul Dirac showed that negative kinetic energy must be included in a complete quantum description of particles; negative $E$ are antiparticles. The general theory of gravity was much more geometrical than analytic. the Minkowski 4D space must be altered to 4D Riemannian space; which became the mathematics of general relativity theory, describing gravity not as a force but as the curvature produced in 4D space-time by matter. The invariants (the laws) in this geometry are tensors; this importance of tensors led to a tremendous increase in tensor analysis, with mathematicians from all countries contributing to its growth. Karl Schwarzschild (1873-1916) at Göttingen: solved Eistein's field equations for a very special case shortly after 1915; which led physicists to the concept of the black hole; 'Schwarzschild radius, $R_s$ David Hilbert (1862-1943): 'Hilbert space': a fictitious space of functions in which the functions play the role of vectors; has an infinite number of dimensions. in quantum mechanics we introduce the concept of the state of a system, such as the state of an electron in an atom; which is the wave function of the electron pictured as a vector in Hilbert space. all the features of the changing state of the electron can be described by the changing Hilbert state vector; this concept unified the Heisenberg matrix mechanics and the Schrödinger wave mechanics. Hilbert may be considered as the last of the great 19C and the first of the great 20C mathematicians who bridged the gap between classical and modern mathematics.

11. 近代数学と新たな物理学: シュレーディンガー (1824): 波動力学     ディラック (1943): アインシュタイン (1917):   ヒルベルト (1902): ノイマン (1930):         ポアンカレ (1883):   ミンコフスキー (1886):     シュヴァルツシルト (1894) シュヴァルツシルト半径   ヒルベルト (1902) ヒルベルト空間

>Top 12. The Evolution of Modern Mathematics: Early decades of 20C: two different demands: to place mathematics on a flawless, logical base and to free it of all inner contradictions and philosophical inconsistencies. advanced mathematics for the proper development of physical theories; theoretical physics is constrained by nature itself whereas mathematics is constrained only by the limits of individual mathematician's imagination. to rid number of any specific quantitative meaning, Cantor introduced the concept of he "aggregate" or "set," which led to modern set theory. set theory became the basis of modern mathematics and analytical tool for all branches of mathematics. Bertrand Arthur William Russel (1872-1970): to place mathematics on a flawless foundation, free of logical inconsistencies. every language has a logical structure (a syntax); we should be able to establish one-to-one correspondence between any language and logic, therefore, between any language and mathematics.; basis of information theory and computer software; ability to express any number on the binomial base (digits 0 and 1 are used) once we have transformed a statement - image, sound, words, mathematical formula into stored information. information theory is to maximize the ratio signal/noise or $\frac{S}{N}$. Radio telescopes developed with ever increasing sensitivity; opened up a radio window to the universe; farther into space than ever before. Radio telescopes have revealed esoteric astronomical objects as quasars, pulsars (neutron stars), radio stars, and active galaxies. 30m paraboloid dish can detect a radio source about 1000 times fainter than by the largest optical telescope. 1955: Russel-Einstein Manifesto - 1957 Pugwash Conference 1948 Claude Shannon (1916-2001): amount of information in terms of the second law of thermodynamics. (the law of entropy) Cybernetics: emerged from theory of information, operations research and theory of games. Operations research; began in WWII Von Neumann, applying nonzero-sum game theory to economics; capitalist economy driven by profit motive. War has been treated by contending parties as a game. War is not a zero-sum game because there is no military action in which one can decide unequivocally how much each side gains or loses. the best players can do is introduce the constraints that are imposed on each side by the losses that each side can sustain. the aim of each side is to force unsustainable losses on the opposing side before suffering such losses itself. Game theory can help in developing such an unsustainable loss strategy. Stinislaw Marcin Ulam (1909-1984): Scientific experimental research called Monte Carlo simulation; in the analysis of complex nuclear phenomena. the physical laws that are required to construct a mathematical model to account for the observations are plugged into the computer as mathematical equations and the computer then simulates as many different variations of the experiment. Ernest Rutherford (1871-1937) and Joseph John Thomson (1856-1940): structure of the atom; raisin-bun model proposed by J.J. Thomson. Rutherford chose gold atoms as the targets fro the alpha particle bullets; most of the alpha particles passed through the gold leaf and came out with their paths only slightly deviated from the straight lines. But every now and then an alpha particle bounced back from the gold leaf as though it had struck an impenetrable wall. Rutherford correctly interpreted this result as evidence that that particular alpha particle had been repelled by a very strong positive charge; the nucleus of an atom positively charged. Fractals and chaos: Benoît B. Mandelbrot (1924-2010): Fractal concept; introduced by B. Mandelbrot; closely related to the group concept which is produced by the unlimited iterations of a particular geometric operation. Iteration of a given function; $f(x)=x^2, \; f(f(x))=(x^2)^2, \; f(f(f(x)))=((x^2)^2)^2$ For $x=1$, all the terms in the sequence equal 1. E. Spiegal: the study of chaos; arose from observations that dynamical systems, such as binary stars or planetary systems. Predictability is not only a matter of having the correct mathematical equations to describe the dynamics of the system but also a matter of knowing about the initial conditions of the system. Erwin Schrödinger (1887-1961); What is life? Genes must be molecules which can change only discontinuously (quantum jumps). this discontinuity ensures that the order in genetic material will persist over hundreds of generations.

12. 近代数学の進化: ラッセル (1921):     シャノン (1958):             ウラム (1946)::     ラザフォード ( 1904):           マンデルブロ (1967):     シュレーディンガー (1824):

>Top13. Whither Mathematics: Mathematical activities that will be avidly pursued: solving great problems that have challenged and defied mathematicians fro generations in every branch of mathematics. improving mathematical techniques and rigor in current mathematics; improving current mathematics as a tool for scientists and engineers in almost every phase of science and technology. Theory of numbers; unproved theorems: finding a general formula for the distribution of prime numbers. (a formula that gives the number of primes below any given integer) proving that, however far out one may go in number system, two prime numbers exist that differ by 2 (e; the primes 29 and 31) finding a formula for prime numbers. Wolfgang Ernst Pauli (1900-1958): Pauli principle; spin theory; structure of matter Discussion of symmetry: This symmetry states that no two sets of quantum integers assigned to the electrons in any atom can be identical; Pauli exclusion principle. Proceeding from atoms to molecules we discover that symmetry again plays the dominant role in molecular structure. Structure of crystals; beauty is the manifestation to our minds of the highest form of symmetry; the most sublime example of this beauty is the human mind itself; all interrelated to each other by a complex symmetry. Living organisms in nature that are most appealing to our sense of beauty are those that are most symmetrical in their structures and colors. All aesthetics and even ethics stem from symmetry and from mathematics. Mathematics is the study of the interrelationships of ideal elements; points, lines, planes numbers, whereas beauty, ethics, and aesthetics are amorphous concepts that have as many different definitions and interpretations.

13. 数学はどこへ行くのか？: パウリ (1929):     対称性の議論

Comment

It is said beauty and luck seldom go together. In the case of mathematicians, I observe that ability and luck seldom go together. The median year (half of life) is written after the name of a mathematician.

美人薄命というが、数学者の場合は偉人薄命かも知れない。 数学者名の後の年次としては寿命の半数の年を記入。