Mathematics Review (II/B/III/C)
Cat: SCI
Pub: 2017
#1702a
Compiled by Kanzo Kobayashi
17214u/18403r
Russian
English
Remarks
0. 序文:
0. Introduction:
>Top
1. 整式と分数式:
分数は有理数の一般表現。割り切れるか割り切れないかも重要な概念。それは素数概念につながる。
1. Integral expression & Fractional expression:
- $A=BQ+R, \; 0\le r<b$
- $\frac{AC}{BC}=\frac{A}{B}$
- $\frac{A}{C}\pm\frac{B}{C}=\frac{A\pm B}{C}$
- $\frac{A}{B}\times \frac{C}{D}=\frac{AC}{BD}$
- $\frac{A}{B}\div \frac{C}{D}=\frac{A}{B}\times \frac{D}{C}=\frac{AD}{BC}$
- $a+bi=c+di \Longleftrightarrow a=c$ and $b=d$
- $a+bi=0 \Longleftrightarrow a=0$ and $b=0$
- 商: Q=Quatient
- 余り: R=Remainder
- 因数: factor
- 因数分解: factorization
- 約分: reduce a fraction
- 分数
- Symmetric polynominals: $(a_1+a_2+a_3)^n
=\sum(\frac{n!}{k_1!k_2!k_3!}a_1^{k_1}a_2^{k_2}a_3^{k_3})$
- ¶ $(a+b+c)^3$:
- Coefficient of $a^3=\frac{3!}{3!}=1;\; a^2b=\frac{3!}{2!1!}=3;\; abc=\frac{3!}{1!1!1!}=6$
- $\therefore (a+b+c)^3=a^3+b^3+c^3+3(a^2b+ab^2+b^2c+bc^2+c^2a+ca^2)
+6abc$
- ¶ $(a+b+c)^4$:
- Coefficient: $1a^4; 4a^3b; 6a^2b^2; 12a^2bc$; total items 81
- $\therefore a^4+b^4+c^4+4(a^3b+ab^3+b^3c+bc^3+c^3a+ca^3)
+6(a^2b^2+b^2c^2+c^2a^2
)+12(a^2bc+ab^2c+abc^2)$
- ¶ $(a+b)(b+c)(c+a)(a+b+c)$: 4th-order homogenous;
coefficient $0a^4; 1a^3b; 2a^2b^2; 4a^2bc$; total items 81
- $\therefore a^3b+ab^3+b^3c+bc^3+c^3a+ca^3+2(a^2b^2+b^2c^2+c^2a^2)
+4(a^2bc+ab^2c+abc^2)$
- 対称式: symmetric polynominlas
- 斉次式: homogeneous equation
- ¶ $\frac{1}{(x-2)(x-5)}=\frac{a}{x-2}+\frac{b}{x-5}$
- $=\frac{1}{3}(\frac{1}{x-5}-\frac{1}{x-2})$
- ¶ $\frac{1}{(2x-1)(x-2)}$
- $=-\frac{1}{3}(\frac{2}{2x-1}-\frac{1}{x-2})$
- 部分分数分解: decompositon of partial fraction
>Top
2. 二次方程式:
- a
Quadricという表現はどうも馴染めない。2D equationの方がしっくりする。
三次方程式の一般解を巡ってはルネサンス期のイタリアで激しい論朗が展開された。
2. Quadric equation:
- Complex number:
- $i^2=-1$
- Conjugate number:
$\alpha=a+bi \;\text{and}\; \overline{\alpha}=a-bi$
- $\alpha\beta=0 \Longleftrightarrow
\alpha=0 \;\text{or}\; \beta=0$
- $\sqrt{-a}=\pm\sqrt{a}i \;$ ,where $a>0$
- $\sqrt{-1}=\pm i$
- Solution of $ax^2+bx+c=0 \; $is:
- $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
- Solution of $ax^2+2bx+c=0 \; $is:
- $x=\frac{-b\pm\sqrt{b^2-ac}}{a}$
- $D=b^2-4ac \;$, (where $D=$Discriminant)
- $D>0 \Longleftrightarrow$ has 2 different real roots
- $D=0 \Longleftrightarrow$ has real multiple root
- $D<0 \Longleftrightarrow$ has 2 different imaginary roots
- Where $\alpha$ and $\beta$ are 2 roots of $ax^2+bx+c=0$;
- $\alpha +\beta=-\frac{b}{a}, \; \alpha\beta=\frac{c}{a}$
- $ax^2+bx+c=a(x-\alpha)(x-\beta)$
- Where $\alpha +\beta=p, \;\alpha\beta=q$;
- $x^2-px+q=0$
- Where the discriminant is D, and 2 roots are $\alpha$ and $\beta$ of $ax^2+bx+c=0$; when $D\ge 0$:
- $\alpha, \; \beta >0 \Longleftrightarrow \alpha+\beta>0,\; \alpha\beta>0$
- $\alpha, \; \beta <0 \Longleftrightarrow \alpha+\beta<0,\; \alpha\beta>0$
- $\alpha, \; \beta$ are opposire signs $\Longleftrightarrow,\; \alpha\beta<0$
- 複素数: complex number
- 実部/虚部: real/imaginary part
- 純虚数: pure imaginary number
- 共役数: conjugate number
- 式: fractional expression
- 有理式: rational expression
- 既約: Inreducible
- 通分(母): common denominator
- 割り切れる: divisable
- 素数: prime number
- 単位: imaginary unit
- 判別式: Discriminant
- 実数解: real root
- 重解/根: multiple root
- 三重解/根: tripple root (solution)
- 虚数解: imaginary root
- 解(根)と係数の関係: root-coefficient relationship; Vieta's formula
- 異符号: opposite sign
- 一次方程式: liner (1st degree) equation
- 二次方程式: quatratic (2nd degree) equation
- 三次方程式: cubic (3th degree)
- 四次方程式: quartic (4th degree)
- 五次方程式: quintic (5th degree)
- 六次方程式: sextic (6th degree)
- $n$次方程式: nth degree equation
- 連立一次方程式: simultaneous linear functions
>Top
3. 高次方程式:
a
3. High-degree equation
- When an integral expression $P(x)$ is divided by $x-\alpha$, the remainder is the constant $P(\alpha)$.
- When an integral expression $P(x)$ has a factor $x-\alpha$ $\;\Longleftrightarrow\; P(\alpha)=0$
- 3 cube roots of 1 are $x=1, \frac{-1\pm\sqrt{3}i}{2},\; or \; 1, \omega, \omega^2$
- $n$th degree equation has $n$ number of solutions (roots).
- 因数定理: factor theorem
- 剰余定理: remainder theorem
- 因数: factor
- 二乗根(平方根): square root
- 三乗根(立方根)$\:\omega$: cube root
- 四乗根: fourth root
>Top
4. 恒等式と不等式:
a
4. Identity & Inequality:
- When $ax^2+bx+c\equiv a'x^2+b'x+c' \Longleftrightarrow a=a',\: b=b', \: c=c'$
- Generally, $P(x)\equiv Q(x) \Longleftrightarrow $ same degree of each polynomial equation corresponds each other.
- Particularly, $P(x)\equiv 0 \Longleftrightarrow $ each coefficient of $P(x)$ is $0$.
- When $\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}$, then $a:b:c=c':b':c'$.
- $a>b \Longleftrightarrow a-b>0$
- $a>b, \; b>c \Longrightarrow a>c$
- $a>b \Longrightarrow a+c>b+c$
- $a>b, \; c>0 \Longrightarrow ac>bc, \frac{a}{c}>\frac{b}{c}$
- $a>b, \; c<0 \Longrightarrow ac<bc, \frac{a}{c}<\frac{b}{c}$
- Where $a$ is a real number, $a^2\ge 0$
- Particularly, $a^2=0 \Longleftrightarrow a=0$
- Where $a\ge 0, \; b\ge 0$, $
- $\frac{a+b}{2}\ge \sqrt{ab}$; equal is formed when $a=b$.
- When $A>0, \; B>0$, then $A\ge B \Longleftrightarrow A^2 \ge B^2$
- 恒等式: $\equiv$
- 各項: each item/clause
- 係数: coefficient
- 比例式: proportional expression
- 連比: continued ratio
- 相加平均: arithmetic mean
- 相乗平均: geometric mean
>Top
5. 点と線:
点をどう共有するかしないかで線の特徴が表れる。
5. Point & Line:
- The distance of 2 points $A(x_1, y_1), \; B(x_2, y_2) \;$ is:
- $AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
- Particularly, the distance of $P(x, y)$ from the origin:
- $OP=\sqrt{x^2+y^2}$
- Cordinates of the point internally dividing point of $m:n$ is:
- $(\frac{nx_1+mx_2}{m+n}, \; \frac{ny_1+my_2}{m+n})$
- Cordinates of the point externally dividing point of $m:n$ is:
- $(\frac{-nx_1+mx_2}{m-n}, \; \frac{-ny_1+my_2}{m-n})$
- Particularly, cordinates of the midpoint of the line segment $AB$:
- $(\frac{x_1+x_2}{2}, \; \frac{y_1+y_2}{2})$
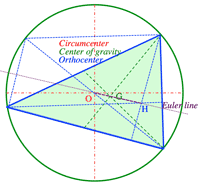
- <Fig.1> Cordinates of the center of gravity of $\triangle ABC, \; A(x_1,y_1), B(x_2,y_2), C(x_3,y_3)$ is:
- $(\frac{x_1+x_2+x_3}{3},\; \frac{y_1+y_2+y_3}{3})$
- Line equation with gradient $m$, passing through the point $(x_1, y_1)$ is:
- $y-y_1=m(x-x_1)$
- Line equation passing through 2 points $(x_1, x_2), (y_1, y_2)$ is:
- $y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1) \; $; when $x_1\neq x_2$
- $x=x_1\; $; when $x_1=x_2$
- Line equation with $x$-intercept $a$, $y$-intercept $b$ is:
- $\frac{x}{a}+\frac{y}{b}$
- Where two lines $y=mx+n,\; y=m'x+n'$,
- Parallel condition: $m=m'$
- Orthogonality condition: $mm'=-1$
- Distance $d$ between the point $(x_1, y_1)$ and the line $ax+bx+c$
- $d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$
- 2点間の距離: distance between 2 points
- 原点: origin (of the coordinate axes)
- 座標: coordinates (of the point)
- 内分点/外分点: internally/externally dividing point
- 中点: midpoint
- 線分: line segment
- 重心: center of gravity
- 垂心: orthocenter
- 内心: inner center
- 外心: circumcenter
- 傍心: excenter
- 勾配: gradient
- 点を通る: pass through the point
- 平行条件: parallel conditon
- 直交(垂直)条件: orthogonality condition
<Fig.1> Euler line
>Top
6. 円:
円は特殊で基本的な図形。車輪や貨幣も円形が基本。
6. Circle:
- Circle equation with radius $r$, centered at the point $(a, b)$ is:
- $(x-a)^2+(y-b)^2=r^2$
- Particularly, circle equation with ratidus $r$, centered at the origin is:
- $x^2+y^2=r^2$
- General formula of circle equation is:
- $x^2+y^2+lx+my+n=0 \; $provided $l^2+m^2-4n>0$
- $(x+\frac{l}{2})^2+(y+\frac{m}{2})^2=\frac{l^2+m^2-4n}{4}$
Center: $(-\frac{l}{2}, -\frac{m}{2}) \;$, radius: $\frac{\sqrt{l^2+m^2-4n}}{2}$
- $\Rightarrow\; (x-a)^2+(y-b)^2=r^2$
- Tangent line at the point of $P(x_1, y_1)$ on the circle $x^2+y^2=r^2$ is:
- $x_1x+y_1y=r^2$
- 円の方程式: circle equation
- 円の方程式 (一般式): general formula of circle equation
- 接線: tangent/tangential line
>Top
7. 軌跡と領域:
境界領域が含まれるか含まれないかは、数学のみならず国家間でも重要となる。
7. Locus & Domain:
- Where line $l$ is expressed as $y=mx+n$
- The domain of $y>mx+n$ is upper part of $l$.
- The domain of $y<mx+n$ is lower part of $l$.
- Where cirld $C$ is expressed as $(x-a)^2+(y-b^2)=r^2$
- The domain of $(x-a)^2+(y-b^2)<r^2$ is inside part of $C$.
- The domain of $(x-a)^2+(y-b^2)>r^2$ is outside part of $C$.
- 軌跡: trajectory
- 領域: domain; region
- 開集合: open set
- 閉集合: closed set
- 境界: boundary
- 象限: quadrant
- 第1象限: first quadrant
- 連立不等式: simultaneous inequality
- 最大値: (global) maximum
- 最小値: (global) minimum
>Top
8. 三角関数:
エジプト文明以来測量など、回転などを想定する物理の記述には必須の技術
8. Trigonometric function:
- Where radium $l$, central angle $\theta$, length of arc $l$, and the area $S$ of a circle:
- $l=r\theta, \; S=\frac{1}{2}r^2\theta=\frac{1}{2}lr$
- Where a cercle with radius $r$ centered at the origin $O$ on a cordinate plane; Trigonometry is defined as:
- $\sin\theta=\frac{y}{r} \; \cos\theta=\frac{x}{r} \; \tan\theta=\frac{y}{x}$
- $\sin^2\theta+\cos^2\theta=1$
- $\tan\theta=\frac{\sin\theta}{\cos\theta}$
- $1+\tan^2\theta=\frac{1}{\cos^2\theta}$
- $\sin(\theta+2n\pi)=\sin\theta,\; \cos(\theta+2n\pi)=\cos\theta,\;\tan(\theta+2n\pi)=\tan\theta$
- $\sin(-\theta)=-\sin\theta, \;\cos(-\theta)=\cos\theta, \;\tan(-\theta)=-\tan\theta$
- $\sin(\theta+\frac{\pi}{2})=\cos\theta,\;\cos(\theta+\frac{\pi}{2})=-ぴ\sin\theta,\;\tan(\theta+\frac{\pi}{2})=-\frac{1}{\tan\theta}$
- $\sin(\theta+\pi)=-\sin\theta,\;\cos(\theta+\pi)=-\cos\theta,\;\tan(\theta+\pi)=\tan\theta$
- 動径: radius vector
- 始線: initial line
- 正/負の向き: positive/negative direction/sense
- ラジアン: radian
- 扇形: sector/fan/pie
- 中心角: central angle
- 弧: arc
- 座標平面: cordinate plane
- 単位円: unit circle
- 正弦/余弦/正接曲線; sine/cosine/tangent curve
- 漸近線: asymptote <G. not fall
- 周期関数: periodic function
- 証明せよ: prove that...
- 証明終わり: Q.E.D. (quod erat demonstrandum
- 故に: therefore; $\therefore$
- なぜなら: because; $\because$
>Top
9. 加法定理:
三角関数は、加法定理が基本になって三角関数の転換が行われる。
9. Trigonometric Addition Theorem:
- <Fig.1> $\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta$
- $\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta$
- $\tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}
{1\mp\tan\alpha\tan\beta}$
- $\sin2\alpha=2\sin\alpha\cos\alpha$
- $\cos2\alpha=cos^2\alpha-\sin^2\alpha=1-2\sin^2\alpha=2\cos^2\alpha-1$
- $\tan2\alpha=\frac{2\tan\alpha}{1-tan^2\alpha}$
- $\sin3\alpha=3\sin\alpha-4\sin^3\alpha$
- $\cos3\alpha=-(3\cos\alpha-4\cos^3\alpha)$
- $\tan3\alpha=\frac{3\tan\alpha-\tan^3\alpha}{1-3\tan^2\alpha}$
- $a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)$
- Conversion formula of addition and product:
- $\sin\alpha\cos\beta=\frac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}$
- $\cos\alpha\sin\beta=\frac{1}{2}\{\sin(\alpha+\beta)-\sin(\alpha-\beta)\}$
- $\cos\alpha\cos\beta=\frac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}$
- $\sin\alpha\sin\beta=-\frac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}$
- Where $\alpha+\beta=A,\; \alpha-\beta=B,$ then:
- $\sin{A}+\sin{B}=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$
- $\sin{A}-\sin{B}=2\cos\frac{A+B}{2}\sin\frac{A-B}{2}$
- $\cos{A}+\cos{B}=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$
- $\cos{A}-\cos{B}=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2}$
- 2直線の成す角: angle between/formed by 2 lines
- 2倍角: double angle
- 関数の合成: composition
- 和差積商: addition/sum; subtraction/difference; multiplication/product; division/quotient
- プラスマイナス: plus or minus
<Fig.1> Addition theorem
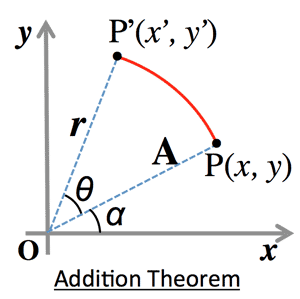
オイラーの公式の活用
Euler's formula
- $e^{i(\alpha+\beta)}=\cos{(\alpha+\beta)}+i\sin{(\alpha+\beta)}$
- $e^{i(\alpha+\beta)}=e^{i\alpha+i\beta}=e^{i\alpha}e^{i\beta}$
$=(\cos{\alpha}+i\sin{\alpha})(\cos{\beta}+i\sin{\beta})$
$=(\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta})+i(\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta})$
- $\therefore \sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}$
- $\cos{(\alpha+\beta)}=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}$
- $e^{2i\theta}=\cos{2\theta}+i\sin{2\theta}$
$=(\cos{\theta}+i\sin{\theta})^2=(\cos^2{\theta}-\sin^2{\theta})+i(2\sin{\theta}\cos{\theta)})$
- $\therefore \sin{2\theta}=2\sin{\theta}\cos{\theta}$
- $\cos{2\theta}=\cos^2{\theta}-\sin^2{\theta}$
- $e^{3i\theta}=\cos{3\theta}+i\sin{3\theta}$
- $=(\cos{\theta}+i\sin{\theta})^3=(\cos^3{\theta}-3\sin^2{\theta}\cos{\theta})+i(3\sin{\theta}\cos^2{\theta)}-\sin^3{\theta})$
$=(4\cos^3{\theta}-3\cos{\theta})+i(3\sin{\theta}-4\sin^3{\theta})$
- $\therefore \sin{3\theta}=3\sin{\theta}-4\cos^3{\theta}$
- $\cos{3\theta}=4\cos^3{\theta}-3\cos{\theta}$
>Top
10. 指数関数:
大きな数字はこの指数表現によって扱いが簡便になる
10. Exponential function:
- $a^ma^n=a^{m+n},\; a^m\div a^n=a^{m-n}$
- $(a^m)^n=a^{mn}$
- $(ab)^n=a^nb^n,\; (\frac{a}{b})^n=\frac{a^n}{b^n}$
- $a^0=1,\; a^{-n}=\frac{1}{a^n}$
- Where $a>0,\;b>0$, and $m, n, p$ are positive integers:
- $\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab},\; \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
- $(\sqrt[n]{a})^m=\sqrt[n]{a^m},\; \sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$
- $\sqrt[np]{a^{mp}}=\sqrt[n]{a^m}$
- Where $a>0$, and $m$ is an integer, and $n$ is a positive integer:
- $a^{\frac{m}{n}}=\sqrt[n]{a^m}$
- Where $a>0,\;b>0$, and $p, q\:$ are rational numbers:
- $a^pa^q=a^{p+q},\; a^p\div a^q=a^{p-q}$
- $(a^p)^q=a^{pq}$
- $(ab)^p=a^pb^p,\; (\frac{a}{b})^p=\frac{a^p}{b^p}$
- Exponential function:
- Domain is entire real numbers, and range of the function is entire positive real numbers;
- The exponential function pass the point $(0,1)$, and $x$-axis becomes an asymptote.
- When $a>1$, then: $p<q \Longleftrightarrow a^p<a^q$
- When $0<a<1$, then:$p<q \Longleftrightarrow a^p>a^q$
- 指数関数: exponential function
- 累乗根: radical root
- $x$の$n$乗: to the $n$th power
- 対数の底: base of a logarithm
- 自然対数: natural logarithm; the base is Napier constant $e=2.71828...$
- 定義域: domain
- 変数の領域: range of variable
>Top
11. 対数関数:
対数表や計算を容易にすることで、天文計算などに有用だった。
11. Logarithmic function:
- When $a>0, \;a\neq 1,\; M>0, \; then:$
- $\log_a{M}=p \Longleftrightarrow a^p=M$
- When $a>0, \;a\neq 1,\; M>0, \; N>0 \;then:$
- $\log_a{MN}=\log_a{M}+\log_a{N}$
- $\log_a{\frac{M}{N}}=\log_a{M}-\log_a{N}$
- $\log_a{M^r}=r\log_a{M}$
- Particularly,
- $\log_a{\frac{1}{N}}=-log_a{N}, \; \log_a{\sqrt[n]{M}}=\frac{1}{n}\log_a{M}$
- When $a, b, c>0, \; a\neq 1, c\neq 1$, then:
- $\log_a{b}=\frac{\log_c{b}}{\log_c{a}}$
- The domain of logarithmic function is the enitre positive real numbers, whose range is the entire real numbers.
- The graph pass through the point $(1,0)$, and y-axis is the asymptote
- When $a>0, y=\log_a{x} $ is an increasing function.
$0<p<q\; \Longleftrightarrow \log_a{p}<\log_a{q}$
- When $0<a<1, \; y=\log_a{x} $ is an decreasing function.
$0<p<q\; \Longleftrightarrow \log_a{p}>\log_a{q}$
- 定義域: domain
- 値域: range
- 漸近線: asymptote
- 増加関数: increasing function
- 減少関数: decreasing function
>Top
12. 微分:
英独の二人の天才が発明。0ではないが0に近づく極微量を考えることで変化を捉え物理などの発展に寄与した。当時の聖職者はこの極微量をお化けと呼んだ。
12. Differential calculus:
- When $x \rightarrow a$ , then $\; f(x)\rightarrow\alpha$
- $\displaystyle\lim_{x\to a}f(x)=\alpha$
- Definition of derivative:
uy
When $x=a \rightarrow x=a+h \;$ then the average rate of change of $y=f(x)$ is:
- $\frac{f(a+h)-f(a)}{h}$
- When $h \rightarrow 0$, limit of the average rate of change is:
- $f'(a)=\displaystyle\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ (differential function)
- Differenctial function of $x^n \;$is:
- $(x^n)'=nx^{n-1}$
- $c$ is constant, $y=c \;$ then: $y'=0$
- $k$ is constant, $y=kf(x)\;$ then: $y'=kf'(x)$
- $y=f(x) \pm g(x)$ , then $y'=f'(x)\pm g'(x)$
- $y=f(x)g(x)$, then $y'=f'(x)g(x)+f(x)g'(x)$
- let, $f(x+h)\simeq hf'(x); g(x+h)\simeq hg'(x)$
- $\therefore f(x+h)g(s+h)\simeq h{f'(x)g(x)+f(x)g'(x)};\; h^2$ is negligible.
- $y=\frac{1}{f(x)}$, then $y'=-\frac{f'(x)}{f^2(x)}$
- $y=\frac{f(x)}{g(x)}$, then $y'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}$
- $y=\log{x},\; x=e^y,\; \frac{dx}{dy}=e^y$
$\therefore \frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}=\frac{1}{e^y}=\frac{1}{x}$
- $y=\sin{x},\; y'=\displaystyle\lim_{h\to 0}\frac{\sin{x+h}-\sin{x}}{h}
=\displaystyle\lim_{h\to 0}\frac{\sin{x+h}-\sin{x}}{h}
=\displaystyle\lim_{h\to 0}\frac{\sin{x}(\cos{h}-1)+\cos{x}\sin{h}}{h}
$
- here, $\displaystyle\lim_{h\to 0}\frac{\cos{h}-1}{h}=0;\;
\displaystyle\lim_{h\to 0}\frac{\sin{h}}{h}=1$
- $\therefore y'=\cos{x}$
- or, $y'=\displaystyle\lim_{h\to 0}\frac{\sin{x+h}-\sin{x}}{h}$
$=\displaystyle\lim_{h\to 0}\frac{2\sin{\frac{h}{2}}\cos{(x+\frac{h}{2})}}{h}$
$=\displaystyle\lim_{h\to 0}
\frac{\sin{\frac{h}{2}}}{\frac{h}{2}}\cos{(x+\frac{h}{2})}$
$=\cos{x}$
- $(a^x)'=\displaystyle\lim_{h\to 0}\frac{a^{x+h}-a^x}{h}
=a^x\displaystyle\lim_{h\to 0}\frac{a^h-1}{h}
=a^x\displaystyle\lim_{h\to 0}\frac{e^{\log a^h}-1}{\log a^h}\frac{\log a^h}{h}
=a^x・1・\log a$
- here, $a^h=e^{\log a^h}$; and $\displaystyle\lim_{h\to 0}\frac{e^h-1}{h}=1$
- or, $y=a^x\;\rightarrow \log y=x\log a$
differentiate both sides: $\frac{y'}{y}=\log x$
- $\therefore y'=y\log a=a^x\log a$
- $(e^x)'=e^x$
$a^x=e^{\log a^x}=e^{x\log a}$
- $\therefore (a^x)'=\log a(e^{x\log a})=a^x\log a$
- 微分係数: differential coefficient/ derivative
- 極限値: limit value
- 極微量: infinitesimal
- 平均変化率: average rate of change
- 導関数: differential function
- 定数関数: constant function
基本的な関数の
導関数
高次
導関数
$f(x)$
$f'(x)$
$f(x)$
$f'(x)$
$x^n$
$nx^{n-1}$
$\tan x$
$sec^2 x$
$e^x$
$e^x$
$\cot x$
$-csc^2 x$
$a^x$
$a^x\log{a}$
$\arcsin x$
$\frac{1}{\sqrt{1-x^2}}$
$\log|x|$
$\frac{1}{x}$
$\arccos x$
$-\frac{1}{\sqrt{1-x^2}}$
$\log_a|x|$
$\frac{1}{x\log{a}}$
$\arctan x$
$\frac{1}{1+x^2}$
$\sin x$
$\cos x$
$\mathrm{arccot} x$
$-\frac{1}{1+x^2}$
$\cos x$
$-\sin x$
$f(x)$
$f^{(n)}$
$f(x)$
$f^{(n)}$
$x^\alpha$
$\alpha(\alpha-1)...(\alpha-n+1)x^{\alpha-n}$
$\sin x$
$\sin(x+\frac{n\pi}{2})$
$e^x$
$e^x$
$\cos x$
$\cos(x+\frac{n\pi}{2})$
$\log x$
$(-1)^{n-1}\frac{(n-1)!}{x^n}$
$(f\pm g)^{(n)}$
$f^{(n)}\pm g^{(n)}$
$(fg)^{(n)}=\displaystyle\sum_{k=0}^n\binom{n}{k}f^{(n-k)}g^{(k)}$ (Leibniz rule)
積の
導関数
$(fg)'$
$f'g+fg'$
$(fg)'’$
$f''g+2f'g'+fg''$
$(fgh)'$
$f'gh+fg'h+fgh'$
>Top
13. 導関数の応用:
導関数は、関数から導き出されるDerivativeであり、これによって速度・変位など多くの物理概念が説明できる。
13. Applicationed of derivative:
- Tangential line of $f(x)$ at the point of $(a, f(a)$:
- $y-f(a)=f'(a)(x-a) \;$ (a: point of contact); f'(x): gradient)
- Increase/decrease of $f(x)$ in the interval:
- when $f'(x)>0\; \Longrightarrow f(x)$ increases in the interval.
- when $f'(x)<0\; \Longrightarrow f(x)$ decreases in the interval.
- Local maximum/minimum:
- when $f'(x)=0, \; f'(x)>0 \; (x<a),\; f'(x)<0\; (x>a)$
$\Longrightarrow f(a)$ is local maximum.
- when $f'(x)=0, \; f'(x)<0\; (x<a),\; f'(x)>0\; (x>a)$
$\Longrightarrow f(a)$ is local minimum.
- 接線: tangent; tangential line
- 接点: point of contact
- 勾配: gradient; grade
>Top
14. 積分:
積分は微分の逆操作として面積など応用範囲が広い
14. Integral calculus:
- Indefinite integral:
- $\int f(x)dx=F(x)+C\;\; (F(x)$ is primitive function; C is constrant)
- $\int x^ndx=\frac{1}{n+1}x^{n+1}+C$
- $\int kf(x)dx=k\int f(x)dx$
- $\int \{f(x)dx\pm g(x)\}dx=\int f(x)dx\pm \int g(x)dx$
- Definite integral:
- $\int_a^b f(x)dx=\bigl[F(x)\bigr]_a^b=F(b)-F(a)$
- $\int_a^b kf(x)dx=k\int_a^b f(x)dx$
- $\int_a^b \{f(x)dx\pm g(x)\}dx=\int_a^b f(x)dx\pm \int_a^b g(x)dx$
- Features of definite integral
- $\int_a^a f(x)dx=0$
- $\int_b^a f(x)dx=-\int_a^b f(x)dx$
- $\int_a^c f(x)dx+\int_c^b f(x)dx=\int_a^b f(x)dx$
- Definite integral and differentiation:
- $\int_a^x f(t)dt=\bigl[F(t)\bigr]_a^x=F(x)-F(a)$
- $\frac{d}{dx}\int_a^x f(t)dt=f(x)$
- Definite integral and area:
- $S=\int_a^b f(x)dx \;\; (F\ge 0; \; a\le x\le b)$
- When $f(x)\ge g(x); \; a\le x\le b; S$ is surrounded by $y=f(x),\; y=g(x),\; x=a,\; x=b)$
$S=\int_a^b \bigl\{ f(x)-g(x)\bigr\} dx$
- 原始関数: primitive function
- 積分定数: integral constant
>Top
15. <B> 数列:
数列は無限の世界に続く道筋。1, 2, ..., n, ..., ∞というようにn番目の駅を把握すると∞への展望が開けてくる。
15. Differential function:
- Arimetic sequence:
- $a_n=a+(n-1)d$
- Geometric sequence:
- $a_n=ar^{n-1}$
- Sum of power:
- $\displaystyle\sum_{k=1}^n c=nc$
- $\displaystyle\sum_{k=1}^n k=\frac{1}{2}n(n+1)$
- $\displaystyle\sum_{k=1}^n k^2=\frac{1}{6}n(n+1)(n+2)$
- $\displaystyle\sum_{k=1}^n k^3=\bigl\{\frac{1}{2}n(n+1)\bigr\}^2$
- Difference sequence:
- $b_n=a_{n+1}-a_n \; (n=1, 2, 3, ....)$
- $a_n=a_1+\displaystyle\sum_{k=1}^{n-1}b_k \;\; (n\ge 2)$
- 数列: sequence
- 級数: series
- 初項: initial item
- 末項: last item
- 第n項: $n$th item
- 一般項: general item
- 公差: common difference
- 無限数列: infinite sequence.
- 等差数列: arithmetic sequnece
- 階差数列: difference sequence
Maclaurin series
- $f(x)=\displaystyle\sum_{k=0}^{\infty}f^{(k)}(0)\frac{x^k}{k!}
=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\frac{f^{(3)}(0)}{3!}x^3+\dots$
- $\sin x=\displaystyle\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k+1}}{(2k+1)!}
=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots$
- $\cos x=\displaystyle\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k}}{(2k)!}
=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots$
- $e^x=\displaystyle\sum_{k=0}^{\infty}\frac{x^k}{k!}
=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\dots$
- $\log (1+x)=\displaystyle\sum_{k=0}^{\infty}(-1)^k\frac{x^{k+1}}{k+1}
=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\dots$
Taylor series
- $f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2!}f''(x_0)(x-x_0)^2+\frac{1}{3!}f^{(3)}(x_0)(x-x_0)^3+\dots$
$=\displaystyle\sum_{n=0}^{\infty}\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n$
>Top
16. 漸化式
前後の関係を明らかにするとその関係はどこまでも続くドミノ理論となる。
16. Recurrence equation
- Where $p, q$ is constant, and $p\neq 1:$
- $a_{n+1}=pa_n+q=a_{n+1}-\alpha=p(a_n-\alpha)\;$
- $a_{n+1}=pa_n-p\alpha+\alpha$
- $\therefore \alpha=p\alpha+q \;\; (q\neq 1)$
- 数学的機能法: proof by mathematical induction
>Top
17. 平面ベクトル
ベクトルは、方向と量を表した非常に便利な概念。また図形が動的に理解できるようになる。
またベクトルの内積の概念は、ベクトルとスカラー間、ベクトル間の角度など新たな領域を広げた。
17. 2D vector
- Vector must
adhere to the addition axiom:
- $\vec{a}+\vec{b}=\vec{b}+\vec{a} \; $ (Associativity)
- $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c}) \; $ (Commutativty)
- $\vec{a}+\vec{0}=\vec{a} \;$ (Identity element)
- $\vec{a}+(-\vec{a})=\vec{0}\;$ (Inverse elements)
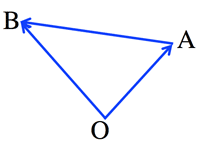
- Vector subtraction: (>Fig.1)
- $\vec{AB}=\vec{OB}-\vec{OA}$
- Multiplicartion by scalar:
- $|m\vec{a}|=|m||\vec{a}|$
- $m(n\vec{a})=(mn)\vec{a}$
- $(m+n)\vec{a}=m\vec{a}+n\vec{a}$
- $m(\vec{a}+\vec{b})=m\vec{a}+m\vec{b}$
- Vector component:
- $\vec{a}=a_1\vec{e_1}+a_2\vec{e_2}=(a_1, a_2)$
- $|\vec{a}|=\sqrt{{a_1}^2+{a_2}^2}$
- Computing element:
- $(a_1, a_2)\pm (b_1,b_2)=(a_1\pm b_1, a_2\pm b_2)$
- $m(a_1, a_2)=(ma_1, ma_2)\;\; (m=$ real number)
- Coordinates and vector component:
- $\vec{AB}=(b_1-a_1, b_2-a_2)$
- $|\vec{AB}|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2}$
- Vector inner product:
- $\vec{a}・\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
- $\vec{a} \perp \vec{b} \Longleftrightarrow \vec{a}・\vec{b}=0$
- Feature of inner product:
- $\vec{a}・\vec{b}=\vec{b}・\vec{a}$
- $\vec{a}・\vec{a}=|\vec{a}|^2, \; |\vec{a}|=\sqrt{\vec{a}・\vec{a}}$
- $|\vec{a}・\vec{b}|\le |\vec{a}||\vec{b}|$
- Component of inner product:
- $\vec{a}・\vec{b}=a_1b_1+a_2b_2$
- $\cos\theta=\dfrac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{a_1b_1+a_2b_2}
{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}}$
- Feature of inner product:
- $(t\vec{a})・\vec{b}=t(\vec{a}・\vec{b})=\vec{a}・(t\vec{b})$
- $\vec{a}・(\vec{b}+\vec{c})=\vec{a}・\vec{b}+\vec{a}・\vec{c}$
- $(\vec{a}+\vec{b})・\vec{c}=\vec{a}・\vec{c}+\vec{b}・\vec{c}$
- Linear independent $\Longleftrightarrow \vec{a}, \vec{b}\neq\vec{0}$ and $ \vec{a}\nparallel\vec{b}$
- Where $\vec{a}, \vec{b}$ are linear independent:
- $m\vec{a}+n\vec{b}=\vec{0} \Longrightarrow m=n=0$
- Any vector on a plane can be uniquely expressed as $m\vec{a}+n\vec{b}$
- 可換律: associativity
- 結合律: commutativity
- 単位元の存在: identity element
- 逆元の存在: inverse elements
- ベクトル成分: vector component
- ベクトルの内積: inner product; scalar product
- 一次独立: linear independent
- 一次従属: linear dependent
<Fig.1> ベクトルの減法: vector subtraction
>Top
18. ベクトルの応用
$\vec{AB}
=\vec{b}-
\vec{a}$は、一旦原点に戻ってからB点に行くイメージ。
18. Application of vector:
- Feature of inner product:
- $(t\vec{a})・\vec{b}=t(\vec{a}・\vec{b})=\vec{a}・t\vec{b}$
- $\vec{a}・(\vec{b}+\vec{c})=\vec{a}・\vec{b}+\vec{a}・\vec{c}$
- $(\vec{a}+\vec{b})・\vec{c}=\vec{a}・\vec{c}+\vec{b}・\vec{c}$
- Where, $\vec{a}, \vec{b}$ are linear independent:
- $m\vec{a}+n\vec{b}=\vec{0} \Longrightarrow \; m=n=0$
- Any vector on a plane can be uniquely expressed as $m\vec{a}+n\vec{n}$
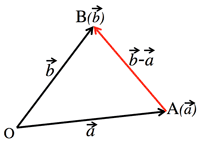
- <Fig.1> Position vector:
- $\vec{AB}=\vec{b}-\vec{a}$
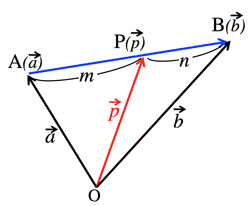
- <Fig.2> Internally/externally dividing point:
- $\vec{p}=\dfrac{n\vec{a}\pm m\vec{b}}{m\pm n}$
- Particularly, the midpoint of line segment $AB$ is: $\dfrac{\vec{a}+\vec{b}}{2}$
- Paticularly, the center of graity of $\triangle ABC$
$\vec{g}=\dfrac{\vec{a}+\vec{b}+\vec{c}}{3}$
- Three points on a same line $\Longleftrightarrow \vec{AC}=m\vec{AB},\;(m $ is real number)
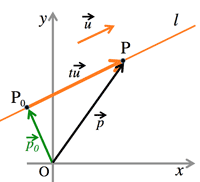
- <Fig.3> Direction vector:
- $\vec{P_0P}\parallel\vec{u}$ or \vec{P_0P}=\vec{0}$
- $\vec{p-p_0}=t\vec{u}, \;(\exists t=$ real number)
- $\vec{p}=\vec{p_0}+t\vec{u}$
- Vector equation of a line passing two point $A(\vec{a}), B(\vec{b}):$
- $\vec{p}=(1-t)\vec{a}+t\vec{b}$
- $\vec{p}=s\vec{a}+t\vec{b}\;\; (s+t=1,\; s\ge 0,\; t\ge 0)$
- A line and normal vector passing $P_0(\vec{p_0})$:
- $\vec{n}・(\vec{p}-\vec{p_0})=0$
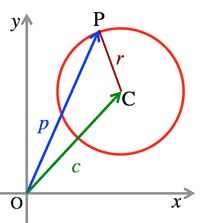
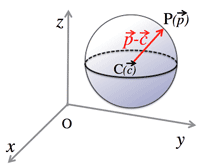
- <Fig.4> Vector equation of a circle centering $C(\vec{c})$, with radius $r$
:
- $|\vec{p}-\vec{c}|=r$
- $(\vec{p}-\vec{c})・(\vec{p}-\vec{c})=r^2$
- where $\vec{p}=(x, y), \; \vec{c}=(a, b),$
$(x-a)^2+(y-b)^2=r^2$
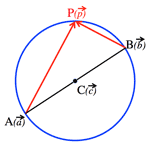
- ¶ <Fig.4b> $AB$ is diameter of a circle:
- $\vec{AP}\perp\vec{BP} \Longleftrightarrow \vec{AP}・\vec{BP}=0$
$(\vec{p}-\vec{a})・(\vec{p}-\vec{b})=0$
- <Fig.5> Inner product and area of a triangle:
- $S=\frac{1}{2}|\vec{a}||\vec{b}|\sin\theta$
- where, $\cos\theta=\dfrac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|}$
- $\sin\theta=\sqrt{1-\left(\frac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|}\right)^2}$
- $S=\frac{1}{2}\sqrt{|\vec{a}|^2| \vec{b}|^2-(\vec{a}・\vec{b})^2}$
- <Fig.6> Parallelogram law:
- $AB^2+AC^2=2(AM^2+BM^2)$
- <Fig.7> Orthcenter:
- $\vec{h}・(\vec{c}-\vec{b})=0, \; (\vec{h}-\vec{b})=0$
- $\vec{HC}\perp\vec{AB}$
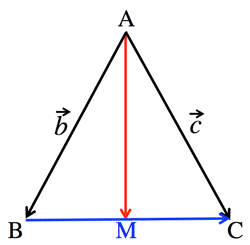
- ¶ s<Fig.8> Isosceles triangle:
- $\vec{AM}=\frac{\vec{b}+\vec{c}}{2}, \; \vec{BC}=\vec{c}-\vec{b}$
- $\vec{AM}・\vec{BC}=|\frac{\vec{b}+\vec{c}}{2}||\vec{c}-\vec{b}|
=\frac{1}{2}(|\vec{c}|^2-|\vec{b}|^2)
=0$
- 線分: line segment
- 方向ベクトル: direction vector
- 法線ベクトル: normal vector
- 一次独立: linear independence
- 一次従属: linear dependence
- 中線定理: parallelogram law
<Fig.1> 位置ベクトル: position vector
<Fig. 2> 内分点/外分点: internally/externally dividing point
<Fig.3> 方向ベクトル: direction vector
<Fig.4b> Vector equation on a circle:
<Fig.4> Circle:
<Fig.5> Triangle:
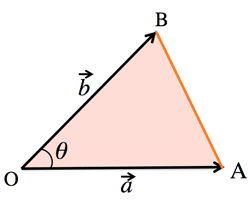
<Fig6> Parallelogram law:
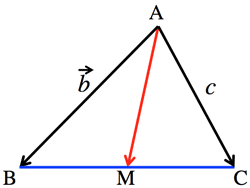
<Fig.7> Orthocenter
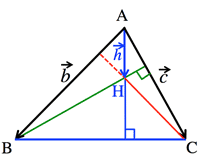
<Fig.8> Isosceles:
>Top
19. 空間ベクトル
ベクトルは高次元になる程、本領を発揮する。
19. 3D vector:
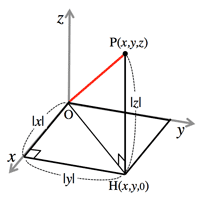
- <Fig.1> Spatial coordinates:
- $OP=\sqrt{x^2+y^2+z^2}$
- $\vec{a}\perp\vec{b} \Longleftrightarrow \vec{b}=m\vec{a}\; (m$ is real number.)
- Any vector \vec{p} in a space can be uniquely expressed as:
$\vec{p}=l\vec{a}+m\vec{b}+n\vec{c}$
- Vector component:
- $\vec{a}=a_1\vec{e_1}+a_2\vec{e_2}+a_3\vec{3_3}=(a_1, a_2, a_3)$
- $|\vec{a}|=\sqrt{{a_1}^2+{a_2}^2+{a_3}^2}$
- Calculation by component:
- $(a_1, a_2, a_3)\pm (b_1, b_2, b_3)=(a_1\pm b_1,\; a_2\pm b_2,\; a_3\pm b_3)$
- $m(a_1, a_2, a_3)=(ma_1, ma_2, ma_3)\;\; (m=$ real number)
- Where $A(a_1, a_2, a_3), B(b_1, b_2, b_3):$
- $\vec{AB}=(b_1-a_1, b_2-a_2, b_3-a_3)$
- $|\vec{AB}|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2}$
- Vector inner product:
- $\vec{a}・\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
- $\vec{a}・\vec{b}=\vec{b}・\vec{a}$
- $\vec{a}・\vec{a}=|\vec{a}|^2, \;\; |\vec{a}|=\sqrt{\vec{a}・\vec{a}}$
- $|\vec{a}・\vec{b}|\le |\vec{a}||\vec{b}|$
- $\vec{a}\perp \vec{b} \Longleftrightarrow \vec{a}・\vec{b}=0$
- Component of inner product:
Where $\vec{a}=(a_1, a_2, a_3),\; \vec{b}(b_1, b_2, b_3):$
- $\vec{a}・\vec{b} \Longleftrightarrow a_1b_1+a_2b_2+a_3b_3$
- $\cos\theta=\dfrac{\vec{a}・\vec{b}}{|\vec{a}||\vec{b}|}
=\dfrac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{{a_1}^2+{a_2}^2+{a_3}^3}
\sqrt{{b_1}^2+{b_2}^2+{b_3}^2}}$
- Feature of inter product:
- $(t・\vec{a})・\vec{b}=t(\vec{a}・\vec{b})=\vec{a}・(t\vec{b})$
- $\vec{a}・(\vec{b}+\vec{c})=\vec{a}・\vec{b}+\vec{a}・\vec{c}$
- $(\vec{a}+\vec{b})・\vec{c}=\vec{a}・\vec{c}+\vec{b}・\vec{c}$
- Innernaly/externally dividing point:
- $\vec{p}=\dfrac{n\vec{a}\pm m\vec{b}}{m\pm n}$
- particularly, the midpoint of line segment $AB: \;\dfrac{\vec{a}+\vec{b}}{2}$
- <Fig.2> Cube in a space:
- $|\vec{p}-\vec{c}|=r$
- particularly, cube at the origin with radius $r: \; x^2+y^2+z^2=r^2$
<Fig.1> 空間座標: spatial coordinates
<Fig.2> Cube
>Top
20. 統計の基礎
統計は数学が一番日常的な表れる場であろう。
20. Basic statistics:
- Arithmetic mean: Excel command [=AVERAGE]
- $\bar{x}=\dfrac{1}{n}\displaystyle\sum_{i=1}^nx_i$
- Median: [=MEDIAN] the value separating the higher half of a data sample or a probaliitly distribution, from the lower half.
- Mode: [=MODE] the value that appears most often in a set of data.
- Deviation:
- $\dfrac{1}{n}\displaystyle\sum_{i=1}^n(x_i-\bar{x})
=$\dfrac{1}{n}\displaystyle\sum_{i=1}^nx_i
-\dfrac{1}{n}\displaystyle\sum_{i=1}^n\bar{x}=\bar{x}-\bar{x}=0
- Variance: [=VAR]
- $s^2=\dfrac{1}{n}\displaystyle\sum_{i=1}^n(x_1-\bar{x})^2
\;\; \left(\bar{x}=\frac{1}{n}\displaystyle\sum_{i=1}^n x_i\right)$
- $s=\sqrt{\dfrac{1}{n}\displaystyle\sum_{i=1}^n(x_1-\bar{x})^2}$
- Correlation coefficient: [=CORREL]
- $r=\dfrac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2} \sqrt{\sum(y_i-\bar{y})^2}}$
- 離散変量: discrete variable
- 度数分布: frequency distribution
- 相対度数: relative frequency
- 正/負の相関: positive/negative correlation
- 散布図: scattergraph
- 算術平均: arithmetic mean
- 中央値: median
- 最頻値: mode
- 偏差: deviation
- 分散: variance
- 相関係数: correlation coefficient
>Top
21. コンピュータ・プログラム
教育では、未だに実用性のないBasicで教えている。せめてJavaScriptやRubyの初歩を教えるのはどうだろうか。
21. Computer program:
- Ranking of programming languages (2016):
Evalutation: 1) easy to Learn, 2) easy to Write (quick to develop), 3) Applicable (object-oriented,
4) Popular, 5) favorable to get Job.
#
Language
Features
Rank
1
JavaScript
- popular for front engineers
- combined with other languages
- mainly Web services
L
W
A
P
J
T
4
3
5
4
5
21
2
Ruby
- a bitl slower processing
- mostly smaller application
- for venture developper
L
W
A
P
J
T
4
5
4
4
4
21
3
Python
- one of Google's major languages (C++, Java, Python)
- used for Facebook development
L
W
A
P
J
T
4
5
4
4
3
20
4
PHP
- for Web application development
- popular in Japan
L
W
A
P
J
T
4
3
3
4
5
19
5
Java
- one of three major languages
- speedy process than PHP/Python/Ruby
L
W
A
P
J
T
2
2
4
5
5
18
6
Swift
- developed by Apple in 2014
- for iOS, Mac application
- shifting from Objective-C to Swift
L
W
A
P
J
T
3
3
3
4
4
17
7
C#
- easier version of C.
- on Windowserver environment
- for PC game development
L
W
A
P
J
T
3
3
4
4
3
17
8
C/C++
- one of three major languages
- relatively difficult to learn
- speedy process than Java
L
W
A
P
J
T
1
2
5
4
4
16
9
ExcelVBA
- on Excel environment
- intuitive
- slow process
L
W
A
P
J
T
5
4
3
2
2
16
10
VB.NET
- easy to learn
- basically on Windows environment.
- a bit old-fashoned
L
W
A
P
J
T
5
3
2
4
1
15
11
Basic
- elementary education
- no practical use any more.
L
W
A
P
J
T
5
1
1
1
1
9
>Top
22. <III> 関数
関数は、数と数との関係。変数の変換など数学の基本が関数論に中に詰まっている。
22. Function:
- A function $f(x)$ takes an input $x$ and return a signel output $f(x)$;
as a machine or black box which returns a corresponding output.
- Where $y=f(x)$ has the inverse funcion $f^{-1}(x)$
$(f^{-1}\circ f)(x)=f^{-1}(f(x))=x$
$(f\circ f^{-1}(y)=f(f^{-1}(y))=y$
- ¶ $y=\frac{e^x-e^{-x}}{2} \Longleftrightarrow y=\log(x+\sqrt{x^2+1})$
- 分数関数: fractional function
- 無理関数: irrational function
- 逆関数: inverse function
>Top
23. 数列の極限
手元でのわずかな計算の違いが、無限遠では無限大に拡散する。
23. Limit of sequence:
- Convergence/divergence of sequece:
- Convergence:
- Divergence:
- $\displaystyle\lim_{n\to\infty}a_n=\infty\; $ (diverges to positive infinity)
- $\displaystyle\lim_{n\to\infty}a_n=-\infty\; $ (diverges to negative infinity)
- fluctuation
- Where sequence $\{a_n\}, \; \{b_n\}$ converge to $\displaystyle\lim_{n\to\infty}a_n=\alpha, \; \displaystyle\lim_{n\to\infty}b_n=\beta$ respectivey:
- $\displaystyle\lim_{n\to\infty}ka_n=k\alpha,\; (k=$ constant.)
- $\displaystyle\lim_{n\to\infty}(a_n\pm b_n)=\alpha\pm \beta$
- $\displaystyle\lim_{n\to\infty}a_nb_n=\alpha\beta$
- $\displaystyle\lim_{n\to\infty}\frac{a_n}{b_n}=\frac{\alpha}{\beta},\; (\beta\neq 0)$
- Squeeze theorem:
- Where sequence $\{a_n\}, \; \{b_n\}$ converge to $\alpha, \beta$ respectively:
$a_n\le b_n \; (n=1, 2, 3, ...) \Longrightarrow \alpha\le\beta$
- Where sequence $\{a_n\}, \; \{b_n\}, \;\{c_n\}$:
$a_n\le b_n\le c_n \; (n=1, 2, 3, ...)$
and $\displaystyle\lim_{n\to\infty}a_n=\displaystyle\lim_{n\to\infty}c_n
=\alpha$, then $\{b_n\}$ also converges:
$
\displaystyle\lim_{n\to\infty}b_n=\alpha$
- Infinite geometric sequence $\{r^n\}$
- $r>1 \Longrightarrow \displaystyle\lim_{n\to\infty}r^n=\infty$
- $r=1 \Longrightarrow \displaystyle\lim_{n\to\infty}r^n=1$
- $|r|<1 \Longrightarrow \displaystyle\lim_{n\to\infty}r^n=0$
- $r\le -1 \Longrightarrow \displaystyle\lim_{n\to\infty}r^n $vibrates, and
$\displaystyle\lim_{n\to\infty}r^n$ does not exist.
- Infinite geometric series, with its intial item $a$, common ration $r$:
- $|r|<1$ converges, and its sum is $\frac{a}{1-r}$
- $|r|\ge 1$ diverges
- Recurring decimal
- Finite decimal or recurring decimal: $\Longrightarrow $Rantional number.
- Infinite non-recurring decimal: $\Longrightarrow $Irrantional number
- Sum of infinite geometric series:
Where
$\displaystyle\sum_{n=1}^{infty}\{a_n\},
\displaystyle\sum_{n=1}^{infty}$ converge respectively to $S, T$:
- $\displaystyle\sum_{n=1}^{infty} ka_n=kS$
- $\displaystyle\sum_{n=1}^{infty}(a_n\pm b_n)=S\pm T$
- Necessary condition of convergence of $\displaystyle\sum_{n=1}^{\infty}a_n$
- $\displaystyle\lim_{n\to\infty}a_n$
- 無限数列: infinite sequence
- 無限級数: infinite series
- 一般項: general item
- 第n項: $n$th item
- 数列の収束/発散: convergence/divergence of sequence
- 極限値: limiting value
- 挟み打ちの原理: squeeze theorem
- 無限等比数列: infinite geometric sequnece
- 循環小数: recurring decimal
- 必要/十分条件: necessary/sufficient condition
- 対偶: contrapostion
- 逆: conversion
- 裏: inversion:
- 否定: negation
- Harmonic series: $1+\frac{1}{2}+\frac{1}{3}+\dots=\displaystyle\sum_{k=1}^{\infty}\frac{1}{k}=\infty$
- $\because 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}>1+\frac{1}{2}+(\frac{1}{4}+\frac{1}{4})
=1+\frac{1}{2}+\frac{1}{2}
$
- generalize: $\displaystyle\sum_{k=1}^{2^p}\frac{1}{k}\ge 1+\frac{p}{2}; \; p\rightarrow \infty$
>Top
24. 関数の極限
途中の規則性は、極限値を予測する。
開区間と閉区間についても厳しく
24. Limit of function::
- Where $\displaystyle\lim_{x\to a}f(x)=\alpha, \;\displaystyle\lim_{x\to a}g(x)=\beta:$
- $\displaystyle\lim_{x\to a}kf(x)=k\alpha, \; (k=$ constant)
- $\displaystyle\lim_{x\to a}\{f(x)\pm g(x)\}=\alpha\pm\beta$
- $\displaystyle\lim_{x\to a}\{f(x)g(x)\}=\alpha\beta$
- $\displaystyle\lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\alpha}{\beta},\; (\beta\neq 0)$
- <Fig.1a/b> Exponential and logarithmic functions:
- $a>1$
- $\displaystyle\lim_{x\to\infty}a^x=\infty$
- $\displaystyle\lim_{x\to -\infty}a^x=0$
- $\displaystyle\lim_{x\to\infty}\log_a x=\infty$
- $\displaystyle\lim_{x\to +0}\log_a x=-\infty$
- $0<a<1$
- $\displaystyle\lim_{x\to\infty}a^x=0$
- $\displaystyle\lim_{x\to -\infty}a^x=\infty$
- $\displaystyle\lim_{x\to\infty}\log_a x=-\infty$
- $\displaystyle\lim_{x\to +0}\log_a x=\infty$
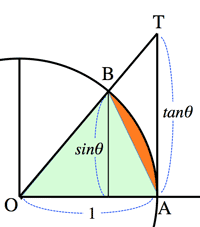
- <Fig.2> Limit of $\frac{\sin\theta}{\theta}$
- $\triangle OAB<fan OAB<\triangle OAT$
- $1<\frac{\theta}{\sin\theta}<\frac{1}{\cos\theta}$
- $1>\frac{\sin\theta}{\theta}<\cos\theta$
- $\therefore \displaystyle\lim_{\theta\to +0}\frac{\sin\theta}{\theta}=1$
- also, $\displaystyle\lim_{\theta\to -0}\frac{\sin\theta}{\theta}=1$
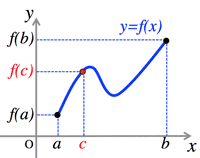
- <Fig.3> Intermediate value theorem:
- $f(x)$ is continuous in a closed interval $[a, b]$, and $f(a), f(b)$ are opposite signs: $\Longrightarrow \; f(x)=0$ has at least one real solution between
$[a, b].$
- 指数関数: exponential function
- 対数関数: logarithmic function
- 開/閉区間: open (a,b) /closed [a,b] interval
- 中間値の定理: intermediate value theorem
- 異符号: opposite sign
<Fig.2> $\frac{\sin\theta}{\theta}$
<Fig.1a> Exponential & logarithmic function:
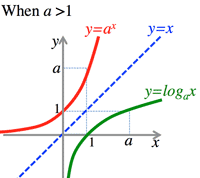
<Fig.1b> Exponential & logarithmic function: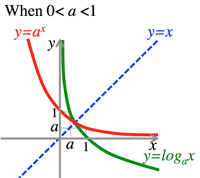
<Fig.3> Intermediate
value theorem:
>Top
25. 微分法
量の変化を求める画期的な方法が17Cに英Newtonと独Leibnitzによって独立に発明され、数学の歴史を変え、かつ物理などその後の科学の発展の強力な道具となった。
25. Differentiation:
- Definition of derivative:
- $f'(x)=\displaystyle\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$
- Features of derivative:
- $(c')=0$
- $\{kf(x)\}'=kf'(x)$
- $\{f(x)\pm g(x)\}'=f'(x)\pm g'(x)$
- $\{f(x)g(x)\}'=f'(x)g(x)+f(x)g'(x)$
- $\{\frac{f(x)}{g(x)}\}'=-\frac{f'(x)g(x)-f(x)g'(x)}{\{g(x)\}^2}$
- particularly, $\{\frac{1}{g(x)}\}'=-\frac{g'(x)}{\{g(x)\}^2}$
- $(x^n)'=nx^{n-1}$
- ¶ Differentialte $y=\log{(\sin(x^3-2))}$
- $\frac{1}{\sin(x^3-2)}・\cos(x^3-2)・3x^2$
- Composite function:
- $\frac{dy}{dx}=\frac{dy}{du}・\frac{du}{dx}$
- $\{f(g(x))\}'=f'(g(x))g'(x)$
- Inverse function:
- $\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}\; (\frac{dx}{dy}\neq 0)$
- 導関数: derivative; 导数 dǎoshù
- 合成関数: composite function
- 高次導関数: higher order derivative
>Top
26. いろいろな導関数
関数の変化から導関数が生まれた。金融商品のデリバティブも将来の変化に連動することで同じルーツ。
26. Various derivatives:
- Derivative of trigonometry:
- $\displaystyle\lim_{\theta\to 0}\frac{\sin\theta}{\theta}=1$
- $(\sin x)'=\lim\frac{\sin{(x+h)}-\sin x}{h}$
$=\lim\frac{2cos{(x+\frac{h}{2})}\sin{\frac{h}{2}}}{h}$
$=\cos x・1=\cos x$
- $(\sin x)'=\cos x$
- $(\cos x)'=-\sin x$
- $(\tan x)'=\frac{1}{\cos^2 x}$
- Derivative of logarithm
- $\displaystyle\lim_{h\to 0}(1+h)^{\frac{1}{h}}=e$
- $(\log x)'=\frac{1}{x}$
- $(\log_a x)'=\frac{1}{x\log a}$
- $(\log|y|)'=\frac{y'}{y}$
- $(e^x)'=e^x$
- $(a^x)'=a^x\log a$
- $(x^{\alpha})'=\alpha x^{\alpha-1},\; (\alpha$ is real number)
- Higher order delivative:
- $y'',\;f''(x),\;\frac{d^2y}{dx^2},\;\frac{d^2}{dx^2}f(x)$
- $y^{(n)},\;f^{(n)}(x),\;\frac{d^ny}{dx^n},\;\frac{d^n}{dx^n}f(x)$
- Expansion of factor theorem:
- $f(x)$ is divisable by $x-\alpha \Longleftrightarrow f(\alpha)=0$
- $f(x)$ is divisable by $(x-\alpha)^2 \Longleftrightarrow f(x)=f'(\alpha)=0$
- $f(x)$ is divisable by $(x-\alpha)^n$
$\Longleftrightarrow f(\alpha)=f'(\alpha)=f''(\alpha)=...=f^{(n-1)}(\alpha)=0$
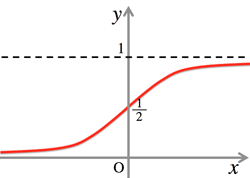
- <Fig.1> Sigmoid function: $f(x)=\frac{1}{a+e^{-ax}} ,\; (a>0)$
- $f'(x)=\frac{ae^{-ax}}{(1+e^{-ax})^2}>0$
<Fig.1> シグモイド: sigmoid
>Top
27. 関数の増減
a
27. Increase/decrease of function
- Equation of tangential line of a cureve $y=f(x)$ passing the point $(a, f(a))$
- $y-f(a)=f'(a)(x-a)$
- Equation of normal line of a cureve $y=f(x)$ passing the point $(a, f(a))$a
- $y-f(a)=-\frac{1}{f'(a)}(x-a)$
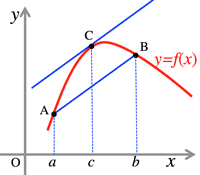
- <Fig.1> Mean value theorem of $f(x)$ which is continuous in $[a, b]$ and differential in $(a, b):$
- $\frac{f(b)-f(a)}{b-a}=f'(c), \; \exists c$ (real number) $a<c<b$
- Increase/decrease of a function $f(x)$:
- where $f'(x)>0, \; (a, b) \Longrightarrow f(x)$ increases in $[a, b]$
- where $f'(x)<0, \; (a, b) \Longrightarrow f(x)$ decreases in $[a, b]$
- where $f'(x)=0, \; (a, b) \Longrightarrow f(x)$ is constant in $[a, b]$
- As long as $f''(x)>0: \;\Longrightarrow y=f(x)$ is covex downward.
- $f''<0: \;\Longrightarrow y=f(x)$ is convex upward.
- When plus/minus sign of $f''(x)$ changes before & after of $x=a \; \Longrightarrow \;$ the point $(a, f(a))$ is the inflection point.
- When $f'(x)=0, \; f''(x)>0 \Longrightarrow $ f(a)$ is local minimum.
- $f'(x)=0, \; f''(x)<0 \Longrightarrow $ f(a)$ is local maximum.
- 上/下に凸/凹: covex/concave upward/downward
- 変曲点: inflection point
<Fig.1> Mean value theorem:
>Top
28. 微分の応用
微分は様々図形の応用だけでなく、物理などに必須の道具となっている。
28. Application of differentiation:
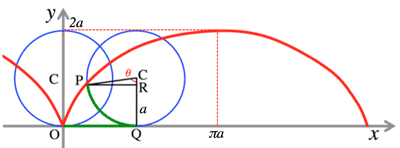
- <Fig.1> Cycloid: circle with radius $a$
- $x=a(\theta -\sin\theta)$
- Parameter representation: where $x=f(t), \; y=g(t)$
- $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{g'(t)}{f'(t)}$
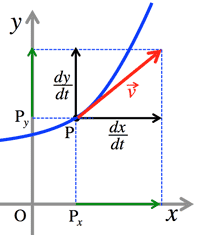
- <Fig.2> Velocity at a point $P (x, y)$ at the time $t$:
- $\vec{v}=(\frac{dx}{dt}, \frac{dy}{dt})$
- $|\vec{v}|=\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}\;\; |\vec{v}|$ is magnitude of velocity.
- $\vec{\alpha}=(\frac{d^2x}{dt^2}, \frac{d^2y}{dt^2})\;\;\alpha$ is acceleration at a point $P (x, y)$ at the time $t$:
- $|\vec{\alpha}|=\sqrt{(\frac{d^2x}{dt^2})^2+(\frac{d^2y}{dt^2})^2}\;\; |\vec{\alpha}|$ is magnitude of acceleration.
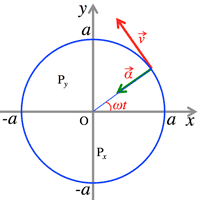
- <Fig.3> Uniform circular velocity: $P$ circulates on a circle $x^2+y^2=a^2$, then the component of the velocity $\vec{v}$ at the point $P$ at the time $t$.
- $\frac{dx}{dt}=-a\omega\sin{\omega t}, \;\;
\frac{dy}{dt}=a\omega\cos{\omega t}$
- $|\vec{v}|=\sqrt{(\frac{dx}{dt})^2+\frac{dy}{dt})^2}$
- $\frac{d^2x}{dt^2}=-a\omega^2\cos{\omega t}, \;\;
\frac{d^2y}{dt^2}=-a\omega^2\sin{\omega t}$
- $|\vec{\alpha}|=\omega^2\sqrt{x^2+y^2}=a\omega^2$
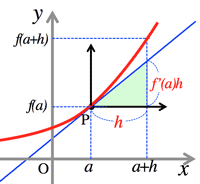
- <Fig.4> Approximation:
- $h\approx 0 \Longrightarrow \; f(a+h)\fallingdotseq f(a)+f'(a)h$
- $x\approx 0 \Longrightarrow \; f(x)\fallingdotseq f(0)+f'(0)x$
- Where $f(x)=x^{\alpha} \; f'(x)=\alpha x^{\alpha-1}$ then,
$(a+h)^{\alpha}\fallingdotseq a^{\alpha}+\alpha a^{\alpha-1}h$
- 媒介変数表示: parameter representation
- 速度: velocity
- 加速度: accelaraion
- 等速円運動: uniform circular motion
- 近似式: approximation
<Fig.1> Cycloid
<Fig.2> Velocity
<Fig.3> Uniform Circular Velocity
<Fig.4> Approximation
>Top
29. 不定積分
被積分関数をintegrand <gerund <gerere+diumされるべきもの。被xxという表現がラテン語にすでに存在していた。微分と積分の関係も被xxの関係になる。
置換積分法は、コアラのように親の袋の中に導関数を抱いているような形。肩車していると$\log$がつく。
29. Indefinite integral:
- When $\alpha\neq -1\;\;
\int x^{\alpha}dx=\frac{1}{\alpha+1}x^{\alpha+1}+C$
- When $t\neq -1\;\;
\int(x-a)^tdx=\frac{1}{t+1}(x-a)^{t+1}+C$
- When $\alpha =-1\;\; \int \frac{1}{x}dx=\log |x|+C$
- $\int\sin xdx=-\cos x+C, \;\; \int\cos xdx=\sin x+ C$
- $\int\frac{1}{\cos^2 x}dx=\tan x+C, \;
\;\int\frac{1}{\sin^2 x}dx=-\frac{1}{\tan x}+C$
- $\int e^xdx=e^x+C, \;\; \int a^xdx=\frac{a^x}{\log a}+C$
- $\int f(ax+b)dx=\frac{1}{a}F(ax+b)+C \;\;, a\neq 0$
- $\int f(x)dx=\int f(g(t))g'(t)dt, \;\; x=g(t)$ (Substitution-1)
$\int f(x)dx=\int f(g(t))\frac{dx}{dt}dt, \;\; x=g(t)$
- $\int f(g(x))g'(x)dx=\int f(u)du, \;\; g(x)=u\;$ (Substitution-2)
- ¶
$\int 2x\sqrt{x^2+1}dx=\int \sqrt{x^2+1}(x^2+1)'dx=\int\sqrt{u}du$
$=\frac{2}{3}i^{\frac{3}{2}}+C$
- ¶ $\int\sin^2x\cos xdx=\int\sin^2x(\sin x)'dx$
$=\int u^2du=\frac{1}{3}u^3+C=\frac{1}{3}\sin^3+C$
- ¶ $\int\sqrt{x+1}(x+2)dx=\int\sqrt{x+1}\{(x+1)+1\}
=\int\{(x+1)^{\frac{3}{2}}+(x+1)^{\frac{1}{2}}\}dx
$
- $\frac{g'(x)}{g(x)}dx=\log |g(x)|+C$
- ¶ $\int\frac{2x}{x^2+5}dx=\int\frac{(x^2+5)'}{x^2+5}dx$
$=\log|x^2+5|+C=\log(x^2+5)+C$
- ¶ $\int\tan xdx=\int\frac{\sin x}{\cos x}dx=\int\frac{-(\cos x)'}{\cos x}dx$
$=-\log|\cos x|+C$
- $\int f(x)g'(x)dx=f(x)g(x)-\int f'(x)g(x)dx\;$ (Partial integration)
- ¶ $\int xe^xdx=\int x・(e^x)'dx=x・e^x-\int 1・e^xdx=xe^x-e^x+C=(x-1)e^x+C$
- ¶ $\int\log xdx=\int(\log x)・(x)'dx=(\log x)・x-\int(\log x)'・xdx$
$=x\log x-\int\frac{1}{x}・xdx=x\log x-x+C$
- ¶ $\int\frac{(x-3)}{(x-1)(x-2)}dx=\int(\frac{2}{x-1}-\frac{1}{x-2})dx$ (decomposition into partial fraction)
$=2\log|x-1|-\log|x-2|+C=\log\frac{(x-1)^2}{|x-2|}+C$
- Indefinite integral of trigonometry:
- ¶ $\int\sin^2xdx=\frac{1}{2}\int(1-\cos2x)dx=\frac{1}{2}(x-\frac{1}{2}\sin2x)+C$
- ¶ $\int\sin4x\cos2xdx=\frac{1}{2}\int\{\sin(4x+2x)+\sin(4x-2x)\}dx$
$=\frac{1}{2}\int(\sin6x+\sin2x)dx=\frac{1}{2}(-\frac{1}{6}\cos6x-\frac{1}{2}\cos2x)+C$
$=-\frac{1}{12}\cos6x-\frac{1}{4}\cos2x+C$
- 原始関数: primitive function
- 被積分関数: integrand
- 積分定数: integral constant
- 部分積分法: partial integration method
- 置換積分: integrateby by substitution
Addition theorem of trigonometry
$\sin^2\alpha=\frac{1-\cos2\alpha}{2}$
$\cos^2\alpha=\frac{1+\cos2\alpha}{2}$
$\sin\alpha\cos\alpha=\frac{\sin2\alpha}{2}$
$\sin\alpha\cos\beta=\frac{1}{2}\{\sin(\alpha+\beta)
+\sin(\alpha-\beta)\}$
$\cos\alpha\cos\beta=\frac{1}{2}\{\cos(\alpha+\beta)
+\cos(\alpha-\beta)\}$
$\sin\alpha\sin\beta=\frac{1}{2}\{\cos(\alpha+\beta)
-\cos(\alpha-\beta)\}$
$f(x)$
$f'(x)$
$\int f(x)dx$
$\sin x$
$\cos x$
$-\cos x+C$
$\cos x$
$-\sin x$
$\sin x+C$
$\tan x$
$\sec^2x=1+\tan^2x$
$-\log{|\cos x|}+C$
$\cot x$
$-\csc^2x=–(1+\cot^2x)$
$\log{|\sin x|}+C$
$\sec x$
$\sec x\tan x$
$\log{|\sec x+\tan x|}+C$
$\csc x$
$-\csc x\cot x$
$-\log{|\csc x+\cot x|}+C$
>Top
30. 定積分
面積が定積分で求められるのは驚きでもある。(リーマン和)
30. Definite integral:
- $\int_a^bf(x)=\bigl[F(x)\bigr]_a^b=F(b)-F(a)$
- Where $x=g(t), \; a=g(\alpha),\; b=g(\beta);$
$\int_a^bf(x)dx=\int_{\alpha}^{\beta}f(g(t))g'(t)dt$
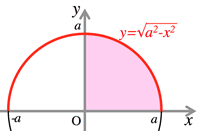
- ¶ <Fig.1> $\int_0^a\sqrt{a^2-x^2}dx, \; a>0:$
- $x=a\sin\theta \Longrightarrow \frac{dx}{d\theta}=a\cos\theta$
$\cos\theta\ge 0$ in the interval $0\leq\theta\leq\frac{\pi}{2}$
$\sqrt{z^2-x^2}=\sqrt{a^2-a^2\sin^2\theta}=\sqrt{a^2\cos^2\theta}
=a\cos\theta
$
- $\therefore \; \int_0^a\sqrt{a^2-x^2}dx=\int_0^{\frac{\pi}{2}}a\cos\theta・a\cos\theta d\theta
=a^2\int_0^{\frac{\pi}{2}}\cos^2\theta d\theta$
$=a^2\int_0^{\frac{\pi}{2}}\frac{1+\cos2\theta}{2}d\theta
=\frac{a^2}{2}\bigl[\theta+\frac{1}{2}\sin2\theta\bigr]_0^{\frac{\pi}{2}}$
$=\frac{1}{4}\pi a^2$
- Even function: $f(-x)=f(x) \;$ while odd function: $f(-x)=-f(x)$
- Where $f(x)$ is even function: $\int_{-a}^af(x)dx=2\int_0^af(x)dx$
while
$f(x)$ is odd function: $\int_{-a}^af(x)dx=0$
- Partial integration of definite integral:
$\int_a^bf(x)g'(x)dx=[f(x)g(x)]_a^b-\int_a^bf'(x)g(x)dx$
(Partial integration)
- ¶ $\int_0^{\frac{\pi}{2}}x\sin xdx=\int_0^{\frac{\pi}{2}}x・(-\cos x)'dx$
$=\bigl[x・(-\cos x)\bigr]_0^{\frac{\pi}{2}}-\int1・(-\cos x)dx=$
$=\bigl[-x\cos x)\bigr]_0^{\frac{\pi}{2}}+\bigl[\sin x\bigr]_0^{\frac{\pi}{2}}=1$
- ¶ $\int_1^ex\log xdx=\int_1^e(\frac{1}{2}x^2)'・\log xdx$
$=\bigl[\frac{1}{2}x^2\log x\bigr]_1^e-\int\frac{1}{2}x^2_・\frac{1}{x}dx=\frac{1}{2}e^2-\frac{1}{2}\int_1^exdx$
$=\frac{1}{2}e^2-\frac{1}{2}\bigl[\frac{1}{2}x^2\bigr]_1^e=\frac{e^2+1}{4}$
- ★Function expressed by definite integral:
$\frac{d}{dx}\int_a^xf(t)dt=\frac{d}{dx}\{F(x)-f(a)\}=f(x), \; a $ is constant.
$\because \; \int_a^xf(t)dt=F(x)-F(a)$ (differentiating the both sides)
- $\frac{d}{dx}\int_{p(x)}^{q(x)}f(t)dt=f(q(x))q'(x)-f(p(x))p'(x)$ (general form)
- ¶ Where $F(x)=\int_a^x(x-t)\cos3tdt, $ Find $F''(x):$
- $F(x)=x\int_a^x\cos3tdt-\int_a^xt\cos3tdt$
- $F'(x)=1・\int/_a^x\cos3tdt+x(\frac{d}{dx}\int_a^x\cos3tdt)-x\cos3x$
$=\int_a^x\cos3tdt+x\cos3x-x\cos3x=\int_a^x\cos3tdt$
- $\therefore \; F''(x)=\cos3x$
- $\displaystyle\lim_{n\to\infty}\displaystyle\sum_{k=1}^nf(x_k)Δx
=\int_a^bf(x)dx$
$
(Δx=\frac{b-a}{n},\; x_k=a+kΔx\;$
(Sectional mensuration)
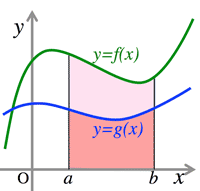
- <Fig.2> Definite integral and Inequality:
Where, $\;f(x)\ge 0$ in the interval $[a, b]$:
- $\int_a^bf(x)dx\ge 0$
- Generally, $\; f(x)\ge g(x)$ in the interval $[a, b], $then:
- $\int_a^bf(x)dx\ge\int_a^bg(x)dx$
- <Fig.3> Wallice's integral: Exponentiation of $\sin x:\; \sin^nx$
- $I_n=\int_0^{\frac{\pi}{2}}\sin^nxdx,\; (n\ge 2)$
$I_n=-\int_0^{\frac{\pi}{2}}\sin^{n-1}x(\cos x)'dx$
$=-\bigl[\sin^{n-1}\cos x\bigr]_0^{\frac{\pi}{2}}$
$+\int(n-1)(\sin^{n-2}x\cos x)\cos xdx$
$=0+(n-1)\int\sin^{n-2}x(1-\sin^2x)dx$
$=(n-1)\int(\sin^{n-2}x-\sin^nx)dx=(n-1)(I_{n-2}-I_n)$
- $\therefore\; I_n=\frac{n-1}{n}I_{n-2}$
- where $I_0=\int_0^{\frac{\pi}{2}}dx=[x]_0^{\frac{\pi}{2}}=\frac{\pi}{2},\;$
$I_1=\int_0^{\frac{\pi}{2}}\sin xdx=[-\cos x]_0^{\frac{\pi}{2}}=1$
- when $(n=)$ even, then:$I_n=\frac{n-1}{n}・\frac{n-3}{n-2}・...・\frac{3}{4}・\frac{1}{2}・\frac{\pi}{2}=\frac{\pi}{2}\frac{(n-1)!!}{n!!}$
- when $(n=)$ odd, then:$I_n=\frac{n-1}{n}・\frac{n-3}{n-2}・...・\frac{4}{5}・\frac{2}{3}・1=\frac{(n-1)!!}{n!!}$
- 下/上端: lower/upper limit
- 偶/奇関数: even/odd function
- 二重階乗: double factorial; 5!!=5・3・1=15
4!!=4・2=8
- 積分論: integration theory
- 不定積分: indefinite integral
- 原始関数: primitive function
- 逆導関数: antiderivative
- a起点不定積分: indefinite integral with base point a
Fig.1 $y=\sqrt{a^2-x^2}$
<Fig.2> Definite integral & Inequality:
<Fig.3 >Wallice's integrals:
$W_0=\frac{\pi}{2},\;W_2=\frac{\pi}{4},\;W_4=\frac{3\pi}{16}
,\;W_6=\frac{5\pi}{32},\;W_8=\frac{35\pi}{56}...$
$W_1=1,\;W_3=\frac{2}{3},\;W_5=\frac{8}{15},\;W_7=\frac{16}{35}...$
>Top
31. 面積・体積
角錐の体積はなぜ正確に角柱の$\frac{1}{3}$なのか小学校以来の疑問だったが積分が必要だったのだ。
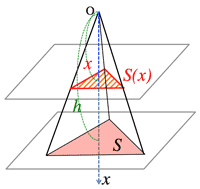
<Fig.6> Pyrmid:
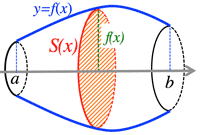
<Fig.7> Rotational body:
31. Area and Volume:
- Where $f(x), g(x)$ are $f(x)\ge g(x)$ in the interval $[a, b]$, then:
$\int_a^b f(x)dx \ge \int_a^b g(x)dx$
- <Fig.1> Where $f(x)\ge 0$ in the interval $[a, b]$, the area $S$ surrounded by $y=f(x), \; y=0,\; x=a,\; x=b$:
- $S=\int_a^bf(x)dx$
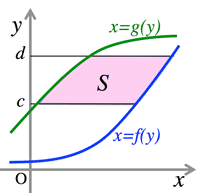
- <Fig.2> Where $f(x)\ge g(x)$ in the interval $[a, b]$, the area $S$ surrounded by $y=f(x),\; y=g(x),\; y=c,\; y=d$:
- $S=\int_c^d\{f(y)-g(y)\}dy$
- <Fig.3> Where $f(x)\ge g(x)$ in the interval $[c, d]$, the area $S$ surrounded by $x=f(y),\; x=g(y),\; x=a,\; x=b$:
- $S=\int_a^b\{f(x)-g(x)\}dx$
- ¶ <Fig.4> Area surrounded by cycloid $x=a(\theta-\sin\theta),\; y=a(1-\cos\theta)$ and
$y=0$ is:
- $S=\int_0^{2\pi a}ydx$
- $\frac{dx}{d\theta}=a(1-\cos\theta)$
- $S=\int_0^{2\pi}a(1-\cos\theta・a(1-\cos\theta)d\theta$
$=a^2\int_0^{2\pi}(1-2\cos\theta+\cos^2\theta)d\theta$
$=a^2\int_0^{2\pi}(1-2\cos\theta+\frac{1+\cos 2\theta}{2})d\theta$
$=a^2\bigl[\frac{3}{2}\theta-2\sin\theta+
\frac{1}{4}\sin 2\theta\bigr]_0^{2\pi}=3\pi a^2$
- <Fig.5> Volume by integral:
- $V'(x)=\displaystyle\lim_{Δx\to 0}\frac{ΔV}{Δx}=\displaystyle\lim_{t\to x}S(t)=S(x)$
- $V=\int_a^bS(x)dx$
- ¶ <Fig.6> Volume of pyramid:
- $S(x): s=x^2: h^2 \Longrightarrow S(x)=\frac{S}{h^2}x^2$
- $V=\int_0^hS(x)x=\int_0^h\frac{S}{h^2}x^2dx$
$\frac{S}{h^2}\bigl[\frac{x^3}{3}\bigr]_0^h=\frac{1}{3}Sh$
- <Fig.7> Rotational body around x-axis of a graph surrounded by $y=f(x),\; y=0,\; x=a,\; x=b$
- $V=\pi\int_a^by^2dx=\pi\int_a^b\{f(x)\}^2dx,\; (a<b)$
- ¶ <Fig.8> Solid torus:
- $V_1=\pi\int_{-r}^r(b+\sqrt{r^2-x^2})^2dx$
- $V_2=\pi\int_{-r}^r(b-\sqrt{r^2-x^2})^2dx$
- $V=V_1-V_2=\pi\int\{(b+\sqrt{r^2-x^2})^2-(b-\sqrt{r^2-x^2})^2\}dx$
$
=4\pi b\int\sqrt{r^2-x^2}dx=4\pi b・\frac{1}{2}\pi r^2=2\pi^2br^2$
- Rotational body around y-axis of a graph surrounded by $x=g(y),\; x=0,\; y=a,\; y=b$
- $V=\pi\int_a^bx^2dy=\pi\int_a^b\{g(y)\}^2dy, \; (a<b)$
- 区分求積法: sectional mensuration
- 回転体: rotational body
<Fig.4> Area of Cycloid:
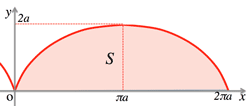
<Fig.5> Volume by integral
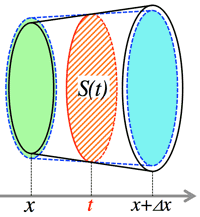
<Fig.8> Solid torus:
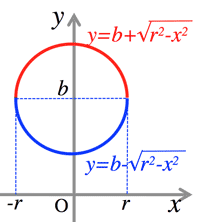
<Fig.1> Area S1
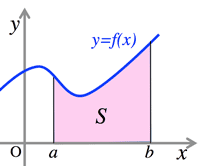
<Fig.2> Area S2
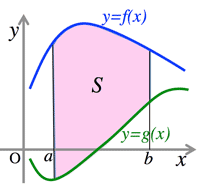
<Fig.3> Area S3
>Top
32. 高次導関数
a
32. Higher order derivative:
- Where $f(x)$ is $n$-th degree polynomial, $\;(a=$constant):
- $f(x)=a_0+a_1(x-\alpha)+a_2(x-\alpha)^2+...+a_n(x-\alpha)^n$
- $f'(x)=a_1+2a_2(x-\alpha)+...+na_n(x-\alpha)^{n-1}$
- $f''(x)=a_2+3・2a_2(x-\alpha)+...+n(n-1)a_n(x-\alpha)^{n-2}$
- ...
- $f^{(n)}(x)=n(n-1)...2・1・a_n$
- Substitute $x=\alpha$ of each equation:
$f(\alpha)=a_0,\;f'(\alpha)=a_1,\;f''(\alpha)=2a_2, ..., f^{(n)}(\alpha)=n!a_n$
- $a_0=f(\alpha),\;a_1=f'(\alpha),\;a_2=\frac{1}{2}f''(\alpha), ..., a_n=\frac{1}{n!}f^{(n)}(\alpha)$
- $\therefore\; f(x)=f(\alpha)+f'(\alpha)(x-\alpha)+\frac{1}{2!}f''(\alpha)(x-\alpha)^2$
$
+\frac{1}{3!}f'''(x-\alpha)^3+...+\frac{1}{n!}f^{(n)}(\alpha)(x-\alpha)^n$
- Taylor expansion:
- $\displaystyle\sum_{n=0}^{\infty}\frac{f^{(n)}(\alpha)}{n!}(x-\alpha)^n$
- Maclaurin expanion:
Where, $f(x)=e^x,\; \alpha=0\;$then, $f^{(n)}(x)=e^x,\; f^{(n)}(0)=1:$
- $e^x=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+...+\frac{1}{n!}x^n+...$
$=\displaystyle\sum_{n=0}^{\infty}\frac{x^n}{n!}\;$ for all $x$.
- Particularly, $x=1$, then:
- $e=1+1+\frac{1}{2!}+\frac{1}{3!}+...+\frac{1}{n!}+...=2.7182818...$
- Binomial theorem:
- $(1+x)^{\alpha}=\displaystyle\sum_{n=0}^{\infty}\binom{\alpha}{n}x^n$ for all $|x|<1\;$ and any comple $\alpha$.
- n次の整式: $n$-th degree polynomial
- テイラー展開/級数: taylor expansion/series
- マクローリン展開: Maclaurin expansion
- 二項定理: binomial theorem
>Top
33. 平均値の定理・ロピタルの定理
a
33. Mean value theorem and L'Hôpital's rule:
- Mean value theorem:
$f(x), g(x)$ are continuous in the interval $[a, b]$ and differentiable in $(a, b)$
- $\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)},\; a<\exists c<b,\; (g'(x)\neq 0, \;g(a)\neq g(b)).$
- L'Hôpital's rule:
- $\displaystyle\lim_{x\to a}\frac{f(x)}{g(x)}
=\displaystyle\lim_{x\to a}\frac{f'(x)}{g'(x)},\; (g'(x)\neq 0$ near $x=a).$
>Top
34. 曲線の長さ
a
34. Length of curve:
- Where the length $s$ of a curve $x=f(t),\; y=g(t), \; (a\le t\le b)$:
- $s=\int_a^b\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt$
$=\int_a^b\sqrt{\{f'(t)\}^2+\{g'(t)\}^2}dt$
- Where the length $s$ of a curve $y=f(x),\; (a\le t\le b)$:
- $s=\int_a^b\sqrt{1+(\frac{dy}{dt})^2}dt$
$=\int_a^b\sqrt{1+\{f'(x)\}^2}dx$
- ¶ <Fig.2> Length of cycloid: $0\le\theta\le2\pi$
$x=a(\theta-\sin\theta),\; y=a(1-\cos\theta),\; (a>0)$
$\frac{dx}{d\theta}=a(\theta-\cos\theta),\;\frac{dy}{d\theta}=a\sin\theta$
$s=\int_0^{2\pi}\sqrt{a^2(1-\cos\theta)^2+a^2\sin^2\theta}d\theta$
$=a\int_0^{2\pi}\sqrt{2-2\cos\theta}d\theta$
$=a\int_0^{2\pi}\sqrt{4\sin^2{\frac{\theta}{2}}}d\theta$
$=2a\int_0^{2\pi}\sqrt{\sin{\frac{\theta}{2}}}d\theta$
$=2a\bigl[-2\cos{\frac{\theta}{2}}\bigr]_0^{2\pi}=8a$
- ¶ <Fig.3> Area (S), Rotation body (V) & length (L) of asteroid:
$x=a\cos^3\theta,\; y=a\sin^3\theta, \; (0\ge\theta\ge\frac{\pi}{2},\; a>0)$
$dx=-3a\cos^2\theta\sin\theta d\theta$
- $S=4\int_0^aydx=4\int_{\frac{\pi}{2}}^0a\sin^3\theta
・(-3a\cos^2\theta\sin\theta d\theta)$
$=12a^2\int_0^{\frac{\pi}{2}}\sin^4\theta\cos^2\theta d\theta$
$=12z^2\int_0^{\frac{\pi}{2}}(\sin^4\theta-\sin^6\theta)d\theta$
$=12a^2(\frac{3}{4}・\frac{1}{2}・\frac{\pi}{2}-\frac{5}{6}・\frac{3}{4}・\frac{1}{2}・\frac{\pi}{2})=\frac{3}{8}\pi a^2$
- $V=2\pi\int_0^{\frac{\pi}{2}}y^2dx$
$=2\pi\int_{\frac{\pi}{2}}^0a^2\sin^6\theta・(-3a\cos^2\theta\sin\theta)d\theta$
$=6\pi a^3\int_0^{\frac{\pi}{2}}\sin^7\theta\cos^2\theta d\theta$
$=6\pi a^3\int_0^{\frac{\pi}{2}}(\sin^7\theta-\sin^9\theta)d\theta$
$=6\pi a^3(\frac{6}{7}・\frac{4}{5}・\frac{2}{3}-\frac{8}{9}・\frac{6}{7}・\frac{4}{5}・\frac{2}{3})=\frac{35}{105}\pi a^3$
- $\frac{dx}{d\theta}=-3a\cos^2\theta\sin\theta,\; \frac{dy}{d\theta}=3a\sin^2\theta\cos\theta$
$\sqrt{(\frac{dx}{d\theta})^2+(\frac{dy}{d\theta})^2}$
$=\sqrt{9z^2\cos^4\theta\sin^2\theta+9a^2\sin^4\theta\cos^2\theta}$
$=\sqrt{9z^2\sin^2\theta\cos^2\theta(\cos^2\theta+\sin^2\theta)}$
$=3a|\sin\theta\cos\theta|=\frac{3}{2}a|\sin2\theta|$
$(0\ge 2\theta\ge\pi \Longrightarrow \sin2\theta\ge 0)$
$\therefore\; L=4・\frac{3}{2}\int_0^{\frac{\pi}{2}}\sin2\theta d\theta=6a\bigl[-\frac{1}{2}\cos2\theta\bigr]_0^{\frac{\pi}{2}}=6a$
- ¶ <Fig.4> Length $s$ of $y=\frac{1}{2}(e^x+e^{-x})=\cosh x\; (0\le x\le a)$ (Catenary)
- $\frac{dy}{dx}=\frac{1}{2}(e^x-e^{-x})$
- $s=\int_0^a\sqrt{1+\frac{1}{4}(e^x-e^{-x})^2}dx$
$=\frac{1}{2}\int_0^a(e^x+e^{-x})dx$
$=\frac{1}{2}\bigl[e^x-e^{-x}\bigr]_0^a=\frac{1}{2}(e^a-e^{-a})$
<Fig.1> Length of curve:
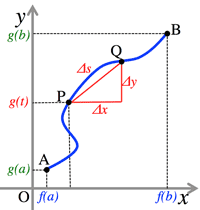
<Fig.2> Cycloid:

<Fig.3> Asteroid:
<Fig.4> Catenary:
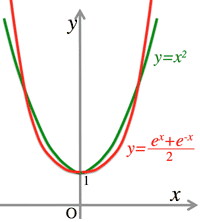
>Top
35. 微分方程式
微分方程式は、微積分法の中で最も応用範囲が広い。社会科学分野でも微分方程式による数学モデルが活用されている。微分方程式の解法は微積分法の腕試しでもある。
35. Differential equation:
- Separation of variables type differential equation:
Where $P(x), Q(x)$ are continuous and $Q\neq 0,$
$\frac{dy}{dx}=P(x)Q(y)$:
- $\int\frac{dy}{Q(y)}=\int P(x)dx$
- ¶ Solve $\frac{dy}{dx}=-xy^2$
- $\int(-\frac{1}{y^2})dy=\int xdx$
$\therefore \frac{1}{y}=\frac{x^2}{2}+C$
$y=\frac{2}{x^2+C}$
- Initial condition $y(\alpha)=\beta$
- $\int_{\beta}^y\frac{dy}{Q(y)}=\int_{\alpha}^xP(x)dx$
- ¶ Solve $\frac{dy}{dx}=-y^2$ with the initial condition $y(0)=1$
- $-\int\frac{dy}{y^2}=\int dx$
$\frac{1}{y}=x+C$
$1=0+C$
- $\therefore\; y=\frac{1}{1+x}$
- Linear 1st-order differential equation:
$\frac{dy}{dx}+p(x)y=0$
- $\frac{dy}{dx}=-p(x)y,\; \frac{dy}{y}=-p(x)dx\;$(Separation of variables)
$y=C\: exp\{-\int p(x)dx\}\;$ (C is constant)
- with initial condition: $y(\alpha)=\beta$
$y=\beta\: exp\{-\int_{\alpha}^xp(x)dx\}$
- ¶ $\frac{dy}{dx}+2xy=0$
- $\int\frac{dy}{y}=\int -2xdx$
$y=e^{-x^2}$
- If $y=u(x),\; y=v(x)\:$are solutions, $y=u(x)+v(x)$ is also solution.
- If $y=u(x)\:$ is solution, $y=ku(x), \;k$ is constant.
- ¶ Temperature of coffee $x$ cools down after $t$ minutes, in proportion to the difference with the room temperature (10ºC); when it was 70ºC after 3 miniutes.
- $\frac{dx}{dt}=-k(x-10)\; (k>0\; k$ is constant)
$\frac{1}{x-10}・\frac{dx}{dt}=-k\; (k-10)>0$
$\int\frac{1}{x-10}・\frac{dx}{dt}dt=-\int kdt$
$\log|x-10|=-kt+C$
$x-10=\pm e^{-kt+C}$
$x=10+C_2e^{-kt}\;\Longrightarrow 90=10+C_2,\; C_2=80$
$x=10+80e^ {-kt}\;\Longrightarrow 70=10+80e^{-3k}\; (t=30,\; x=70)$
$\therefore e^{-3k}=\frac{3}{4}\;,$when $t=6,$
$x=10+80e^{-6k}=10+80・(e^{-3k})^2=10+80・(\frac{3}{4})^2=55$ (ºC)
- ¶ Decay of radioactive element: $t=0, x=x_0$
when will be $x=\frac{x_0}{2}$
$\frac{dx}{dt}=-kx$
$\frac{1}{x}dx=-kdt$
$\int\frac{1}{x}=-\int kdt$
$\log|x|=-kt$
$x=Ce^{-kt}\; \Longrightarrow\; x_0=C$ (t=0, x=x_0)
$x=x_0e^{-kt}\; \Longrightarrow\; \frac{1}{2}=e^{-kt}$
$\therefore, \; -kt=-\log2\;\Longrightarrow\; t=\frac{log2}{k}$
- 1階微分方程式: 1st order differential equation
- 変数分離形: separation of variables
- 初期条件: initial condition
- $e^{f(x)}=exp\{f(x)\}$
- 一般解: general solution
- 特殊解: particular solution
- 特異解: singular solution
- 初期値問題: initial value problem
- 境界値問題: boundary value problem
- 同次形=斉次方程式: homogenious equation
l >Top
36. <C> 行列
a
36. Determinant
- Basic operations
- Addition: $(A+B)_{i,j}=A_{i,j}+B_{i,j} \;$ where $1\le i\le m,\; 1\le j\le n$
- Scalar multiplication: $(cA)_{i,j}=c・A_{i,j}$
- Associativity: $(AB)C=A(BC)$
- Distributivity: $(A+B)C=AC+BC; C(A+B)=CA+CB$
- NOT Commutative: $AB\neq BA$
- Where $A=\pmatrix{a&0\cr 0&0},\; B=\pmatrix{0&1\cr 1&0}$
$AB=\pmatrix{0&1\cr 0&0},\; BA=\pmatrix{0&0\cr 1&0}$
$therefore AB\neq BA$
- If $AB=BA$, which is called exhangeable matrix
- Transpostion: $(A^T)_{i,j}=A_{j,i}$
- Diagonal matrix; Lower triangular matrix; Upper triangular matrix
- Unit matrix and zero matrix:
- $AE=EA=A$
- $AO=OA=O$
- Where $A=\pmatrix{1&2\cr 2&4},\; B=\pmatrix{2&-6\cr -1&3}$
$AB=O$ but $A\neq O,\; B\neq O$
- Cayley-Hamilton theorem:
Where $A=\pmatrix{a&b\cr c&d}, \; A^2-(a+d)A+(ad-bc)E=O$
- ¶ Where $A=\pmatrix{2&3\cr-1&-1}, $ then:
$A^2-(2-1)A+(-2+3)E=0$
$A^2-A+E=0, \; \Longrightarrow A^2=A-E$
$A^3=A^2・A=(A-E)A=A^2-A=(A-E)-A=-E=\pmatrix{-1&0\cr 0&-1}$
- Inverse matrix:
- Where $A=\pmatrix{a&b\cr c&d},\; Δ=ad-bc$
when $Δ\neq 0, \longrightarrow A^{-1}=\dfrac{1}{Δ}\pmatrix{d&-b\cr -c&a}$
when $Δ=0$, then there is no inverse matrix exists.
- ¶ Where 2x2 square matrix$A$ and $B$; when $\exists A^{-1}$ and $\exists B^{-1}:$
$(AB)^{-1}=B^{-1}A^{-1}$
- Similarly, $(ABC)^{-1}=C^{-1}B^{-1}A^{-1}$
- Diagonal matrix:
- Where diagonal matrix $\pmatrix{a&0\cr 0&b},$ n-th power of the diagonal matrix is:
$\pmatrix{a&0\cr 0&b}^n=\pmatrix{a^n&0\cr 0&b^n}$
- ¶ Diagonalize $A=\pmatrix{1&3\cr -2&-4}$
- Eigen value using eigen equation:
$det(A)=\pmatrix{1-\lambda&3\cr -2&-4-\lambda}$
$(1-\lambda)(-4-\lambda)+6=0 \Longrightarrow \lambda=-1, -2$
- Eigen vector:
1) $\lambda=-1:\; \pmatrix{2&3\cr -2&-3}\pmatrix{x\cr y}=\pmatrix{0\cr 0} \Longrightarrow (x,y)=t(3, -2)$
2) $\lambda=-2:\; \pmatrix{3&3\cr -2&-2}\pmatrix{x\cr y}=\pmatrix{0\cr 0} \Longrightarrow (x,y)=t(1, -1)$
- $P=\pmatrix{3&2\cr 1&-1},\;P^{-1}=\pmatrix{1&1\cr -2&-3};\; D=\pmatrix{-1&0\cr 0&-2} \Longrightarrow P^{-1}AP=\pmatrix{-1&0\cr 0&-2}$
- 行列: determinant, matrix
- 要素/成分: element/component
- 行列: $$m$ row/$n$ column
- 転置: transpose
- 階数: rank
- 単位行列: unit matrix
- 交換可能行列: exchangeable matrix
- ケーリー・ハミルトンの定理: Cayley-Hamilton theorem
- 固有ベクトル: eigen vector
- 固有値: eigenvalue
- 固有方程式: eigen equation
- 逆行列: inverse matrix
- 二次正方行列: secondary square matrix
- 対角行列: diagonal matrix
- 対角化する: diagonalize
>Top
37. 行列の応用
a
37. Application of determinant
- Simultaneous linear equations:
- $\cases{2x-5y=9\cr 3x+4y=2}$
$\pmatrix{2&-5\cr 3&4}\pmatrix{x\cr y}=\pmatrix{9\cr 2}$
$\pmatrix{x\cr y}=\dfrac{1}{23}\pmatrix{4&5\cr -3&2}\pmatrix{9\cr 2}=\pmatrix{2\cr -1}$
$\therefore\; x=2,\; y=-1$
- Symmery:
- Symmetric with respect to x-axis:
- $\pmatrix{x'\cr y'}=\pmatrix{1&0\cr 0&-1}\pmatrix{x\cr y}$
- Symmetric with respect to y-axis:
- $\pmatrix{x'\cr y'}=\pmatrix{-1&0\cr 0&1}\pmatrix{x\cr y}$
- Symmetric with respect to the origin:
- $\pmatrix{x'\cr y'}=\pmatrix{-1&0\cr 0&-1}\pmatrix{x\cr y}$
- Symmetric with respect to $y=x$:
- $\pmatrix{x'\cr y'}=\pmatrix{0&1\cr 1&0}\pmatrix{x\cr y}$
- Similarity transformation with respect to the origin:
- $\pmatrix{x'\cr y'}=\pmatrix{k&0\cr 0&k}\pmatrix{x\cr y}$
- Linear transformation:
- $\cases{x'=ax+by\cr y'=cx+dy}$
$\pmatrix{x'\cr y'}=\pmatrix{a&b\cr c&d}\pmatrix{x\cr y}$
- Transformation by inverse matrix:
- $\pmatrix{x'\cr y'}=A\pmatrix{x\cr y}$
$\pmatrix{x\cr y}=A^{-1}\pmatrix{x'\cr y'}$
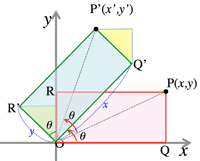
- <Fig.1> Rotation around the origin:
- Where $Q(x,0),\; R(0, y)$
$Q'(x\cos\theta, x\sin\theta),\; R'(-y\sin\theta, y\cos\theta)$
$P'(x\cos\theta-y\sin\theta,\; x\sin\theta+y\cos\theta)$
$\therefore\; \cases{x'=x\cos\theta-y\sin\theta\cr y'=x\sin\theta+y\cos\theta}$
- $\pmatrix{x'\cr y'}= \pmatrix{\cos\theta&-\sin\theta\cr \sin\theta&\cos\theta}\pmatrix{x\cr y}$
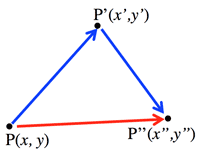
- <Fig.2> Synthetic transformation: $P→P'→P''$
- $\pmatrix{x'\cr y'}=A\pmatrix{x\cr y}$
- $\pmatrix{x''\cr y''}=B\pmatrix{x'\cr y'}$
$\therefore\; \pmatrix{x''\cr y''}=BA\pmatrix{x\cr y}$
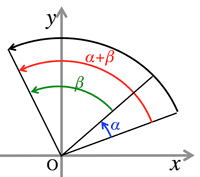
- <Fig.3> Addtion theorem of trigonometry
- $\pmatrix{\cos(\alpha+\beta)&-\sin(\alpha+\beta)\cr \sin(\alpha+\beta)&\cos(\alpha+\beta)}$
$=\pmatrix{\cos\beta&-\sin\beta\cr \sin\beta&\cos\beta}
\pmatrix{\cos\alpha&-\sin\alpha\cr \sin\alpha&\cos\alpha}$
$=\pmatrix{\cos\alpha\cos\beta-\sin\alpha\sin\beta&-\sin\alpha\cos\beta-\cos\alpha\sin\beta\cr \cos\alpha\sin\beta+\sin\alpha\cos\beta&
-\sin\alpha\sin\beta+\cos\alpha\cos\beta}$
- $\therefore \; \cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
$\cos(-\beta)=\cos\beta,\; \sin(-\beta)=-\sin\beta$
- $\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$
$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$
- 連立一次方程式: simultaneous linear equations
- 一次変換:
<Fig.1> Rotation around the origin:
<Fig.2> Synthetic transformation:
<Fig.3> Addtion theorem of trigonometry:
>Top
39. 媒介変数・極座標
媒介変数は2変数を仲立ちする変数で助変数とも呼ばれる。
Excel計算によって描画可能。
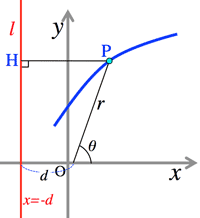
<Fig.9> Polar equation of quadratic:
39. Parameter and polar coordinates:
- Parameter of circle:
- $\cases{x=r\cos t\cr y=r\sin t}$
- <Fig.0> Parameter of ellipse:
- $\cases{x=a\cos t\cr y=b\sin t}$
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
- <Fig.1> Parameter of cycloid:
- $\cases{x=a(t-\sin t)\cr y=a(1-\cos t)}$
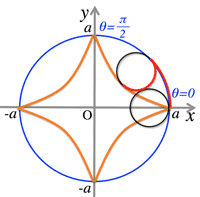
- <Fig.2> Asteroid curve:
- Where, smaller circle with radius $\frac{a}{4}$ rotates inside of a circle with radium $a$:
$\cases{x=a\cos^3\theta\cr y=a\sin^3\theta}$
- <Fig.3> Cardioid:
- Where, a circle with radius $a$ rotates around another circle with radius $a$
$\cases{x=a(1+\cos\theta)\cos\theta\cr y=a(1+\cos\theta)\sin\theta}$
- <Fig.4> Logarithmic spiral:
- $\cases{x=ae^{b\theta}\cos\theta\cr y=ae^{b\theta}\sin\theta}$
- <Fig.5> Lissajous curve:
- Where amplitude $A, B$, angular frequency $a, b$, and phase difference $\delta$
$\cases{x=A\sin(a\theta+\delta)\cr y=B\sin(b\theta}$
- <Fig.6> Lemniscate:
- $\cases{x=2\cos\theta\cr y=2\sin2\theta}, \; (-\pi\le\theta\le\pi)$
- <Fig.7> Involute curve:
- $\cases{x=a(\cos\theta+\theta\sin\theta)\cr y=a(\sin\theta-\theta\cos\theta)}$
- <Fig.8> Folium of Decartes
- $x^3+y^3-3axy=0$
- $\cases{x=\frac{3at}{1+t^3}\cr y=\frac{3at^3}{1+t^3}},\; (t\neq -1)$
- <Fig.9> Polar equation of quadratic curves:
- $\frac{PO}{PH}=e,\; PO=r,\; PH=d+r\cos\theta$
$r=e(d+r\cos\theta)$
$\therefore r=\frac{ed}{1-e\cos\theta}$
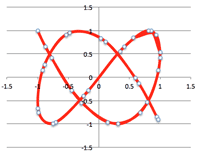
- <Fig.10> Folium curves: (odd is single, but even is double? )
- $r=\sin{(\theta・\frac{n}{d})}$
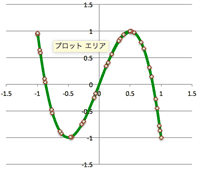
- ¶ <Fig.11> $r=\cos3\theta$
- a
<Fig.0> Ellipse
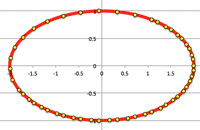
<Fig.5> Lissajous curves:
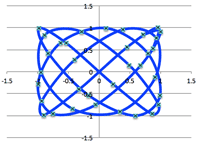
<Fig.1> Cycloid
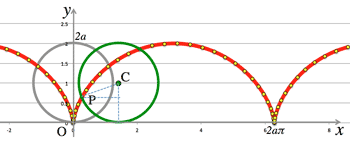
<Fig.2> Asteroid
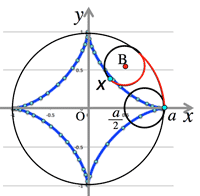
<Fig.3> Cardioid
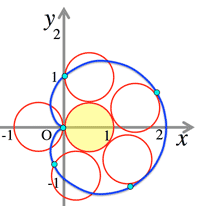
<Fig.4> Logarithmic spiral
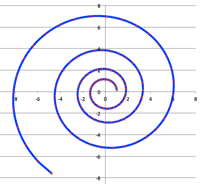
<Fig.6> Lemniscate
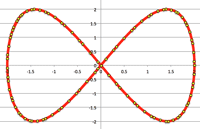
<Fig.7> Involute curve
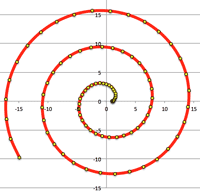
<Fig.8> Folium of Decartes
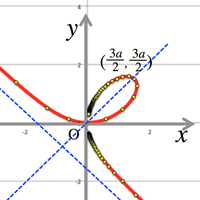
<Fig.11> $r=\cos3\theta$
<Fig.10> $r=\sin n\theta (n=2, 3, 4, 5, 6, 7, 8)$

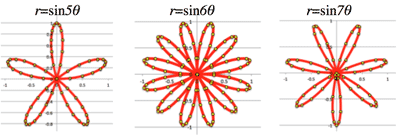
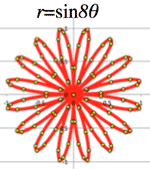
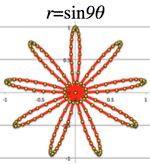

>Top
40. 条件付き確率
Data collecton and analysis are an integral part of our day-to-day actitivties.
40. Conditional probability:
- Permutation:
- ${}_nP_r=\frac{n!}{(n-r)!}$
- Combination:
- ${}_nC_r=\frac{P}{r!}=\frac{n!}{r!(n-r)!}=\binom{n}{r}$
- $(1+x)^n=\displaystyle\sum_{k=0}^n\binom{n}{k}x^k$
- ${}_nC_0+{}_nC_1+{}_nC_2+....+{}_nC_n=2^n$
- ${}_nC_r={}_nC_{n-r}$
- ${}_nC_r={}_{n-1}C_{r-1}+{}_{n-1}C_{r}$ (excluding or including particular one)
- Grouping $(a+b+c=n)$ out of $n: \; {}_nC_a・{}n_{n-a}C_b$
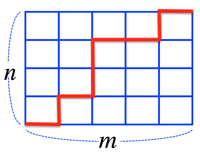
- <Fig.0> Shortest path: ${}_{n+m}C_n=\frac{(n+m)!}{n!m!}$
- Coefficient of $a^pb^qc^r$ of $(a+b+c)^n, \; (p+q+r=n)$
${}_nC_p・{}_{n-p}C_q=\frac{n!}{p!(n-p)!}・\frac{(n-p)!}{q!(n-p-q)!}=\frac{n!}{p!q!r!}$
- Repeated Combination: ${}_nH_r={}_{n+r-1}C_r$
- ${}_nH_r={}_nH_{r-1}+{}_{n-1}H_r$
- <Fig.1> Conditional probability:
- $P(A\cap B)=P(A)P_A(B)$
- $P(A\cap B\cap C)=P(A)P_A(B)P_{A\cap B}(C)$
- $P_A(B)=\frac{P(A\cap B)}{P(A)},\; P(A)\neq 0$
- ¶ Probabilities: $P(A\cap B)=\frac{a}{n},\; P(A)=\frac{a+b}{n},\; P_a(B)=\frac{a}{a+b}$
- $\forall \ A,\; 0\ge P(A)\ge 1$
- Probabilities of universal set and null set are: $P(U)=1,\; P(\emptyset)=0$
- $A, B$ are exclusive events: $P(A\cup B)=P(A)+P(B)$
- $A, B$ are non-exclusive events: $P(A\cup B)=P(A)+P(B)-P(A\cap B)$
- Probalility of complementary set $\overline{A}:\; P(\overline{A})=1-P(A)$
- Multiplation theorem of probability:
- $P(A\cap B)=P(A)・P_A(B)$ b
- $A, B$ are independents: $\;P(A\cap B)=P(A)・P(B)$
- 順列/組合せ: permutation/ combination
- ベン図: Venn's diagram
- 全事象: whole event
- 全体集合: universal set
- 空集合: empty/null set
- 排反事象: exclusive event
- 余事象: complementary set
<Fig.0> Shortest path:
<Fig.1> A and B:
<Fig.2>
$B$
$\overline{B}$
Total
$A$
$a$
$b$
$a+b$
$\overline{A}$
$c$
$d$
$c+d$
Total
$a+c$
$b+d$
$n$
>Top
41. 確率分布
a
41. Probability distribution:
- Where random variable $X: x_1, x_2, ..., x_n$ and probability distribution $P(X=x_i)=p_i, $ then
-
$X$
$x_1$
$x_2$
...
$x_n$
Total
$P$
$p_1$
$p_2$
...
$p_n$
1
- ¶ Probability $X$ of obtainining 2 white balls out of the sack containing 4 white and 3 black balls:
$X_0=\frac{{}_3C_2}{{}_7C_2},\; X_1=\frac{{}_4C_1・{}_3C_1}{{}_7C_2}, \;X_2=\frac{{}_4C_2}{{}_7C_2}$
$X$
$0$
$1$
$2$
Total
$P$
$\frac{1}{7}$
$\frac{4}{7}$
$\frac{2}{4}$
1
- Average of random variables, or expected value: $E(X)=x_1p_1+x_2p_2+...+x_np_n$
- ¶ There are 2 defective in 10 goods. Probability distribution of the number of defective goods $X$ if you pick 3 goods.
$X_0=\frac{{}_8C_3}{{}_{10}C_3}=\frac{7}{15}$
$X_1=\frac{{}_2C_1・{}_8C_2}{{}_{10}C_3}=\frac{7}{15}$
$X_2=\frac{{}_2C_2・{}_8C_1}{{}_{10}C_3}=\frac{1}{15}$
$E(X)=\frac{7}{15}+\frac{2}{15}=\frac{3}{5}$
- Average of random variable $aX+b$:
- $E(aX+b)=aE(X)+b,\;$ (X-m is variance), or $E(X-m)=0,\; (\because E(X)=m)$
- Average of random variable $X^2$:
- $E(X^2)=\displaystyle\sum_{i=1}^n{X_i}^2p_i$
- ¶ Sum of numbers of casting a die:
$E(X^2)=\displaystyle\sum_{i=1}^6(i^2・\frac{1}{6})=\frac{1}{6}(1^2+2^2+...+6^2)=
\frac{91}{6}$
- Variance of random variables:
- Where $p_i$ is the probability of $X=x_i$, and $m$ is the average of $X$:
- $V(X)=\displaystyle\sum_{i=1}^n(x_i-m)^2p_i=E((X-m)^2)=E(X^2)-m^2$
- ¶ Variance of X (sum of numbers of casting a die):
$E(X^2)=\frac{91}{6}$ and $E(X)=m=\frac{7}{2}$
$V(X)=E(X^2)-m^2=\frac{91}{6}-(\frac{7}{2})^2=\frac{36}{12}
- Average, Variance, and SD of $V(X)=aX+b$:
- E(aX+b)=aE(X)+b
- V(aX+b)=a^2V(X)
- \sigma{(aX+b)}=|a|\sigma{(X)}
- ¶ Random variable $Z=\frac{X-m}{\sigma},\; (E(X)=m, SD=\sigma)$
$Z=\frac{X}{\sigma}-\frac{m}{\sigma}=\frac{E(X)}{\sigma}-\frac{m}{\sigma}=0$
$V(Z)=\frac{V(X)}{\sigma^2}=\frac{\sigma^2}{\sigma^2}$
$\sigma(Z)=\sqrt{V(Z)}=1$
- ¶ Stadard measure: $z=\frac{x_i-m}{\sigma}$
- ¶ Standard Score: $H=\frac{10(X-m)}{\sigma}+50$
- Average of sum of random variables:
- $E(X+Y)=E(X)+E(Y)$
- ¶ Casting two dice, and the sum of the numbers of dice:
$E(X+Y)=E(X)+E(Y)=\frac{7}{2}+\frac{7}{2}=7$
- Average of product of independent random variables:
- $E(XY)=E(X)・E(Y)$
- ¶ Casting two dice, and the sum of the numbers of dice:
$E(XY)=E(X)・E(Y)=\frac{7}{2}・\frac{7}{2}=\frac{49}{4}$
- Variance of sum of independent random variables:
- $V(X+Y)=E((X+Y)^2)-E(X+Y)^2$
$=E(X^2+2XY+Y^2)-(E(X)+E(Y))^2$
$=\{E(X^2)+2E(XY)+E(Y^2)\}-\{E(X)^2+2E(X)・E(Y)+E(Y)^2\}$
$=\{E(X^2)-E(X)^2\}+\{E(Y^2)-E(Y)^2\}
$=V(X)+V(Y) $, \;(E(XY)=E(X)・E(Y), (\because X, Y$ are indendent.)
- $V(X+Y)=V(X)+V(Y)$
- Binomial distribution:
- Where probability of occurence $p$ and non-occrence $q=1-p$ of an event $A$; repeat trials $n$ times. Probability $X=r$ will be:
- $P(X=r)={}_nC_rp^rq^{n-r}, \;$ (r=0, 1, 2, ..., n)
$X$
$0$
$1$
...
$r$
...
$n$
total
$P$
${}_nC_0q^n$
${}_nC_1pq^{n-1}$
...
${}_nC_rp^rq^{n-r}$
...
${}_nC_np^n$
1
- ¶ When casting a die 5 times, the probality of pip of one $P(1\le X\le 3)$:
$X$ occurs according to the binominal distribution of $B(5, \frac{1}{6})$
$P(1\le X\le 3)=P(X=1)+P(X=2)+P(X=3)$
$=\binom{5}{1}(\frac{1}{6})(\frac{5}{6})^4
+\binom{5}{2}(\frac{1}{6})^2(\frac{5}{6})^3
+\binom{5}{3}(\frac{1}{6})^3(\frac{5}{6})^2$
$=5・\frac{5^4}{6^5}+10・\frac{5^3}{6^5}+10・\frac{5^2}{6^5}=\frac{4625}{7776}=\fallingdotseq 0.595$
- ¶ Average & Variance of binomial distribution:
- When casting a die 4 times, the random variable $X_i=1 when the pip of one, and x_i=0 the pip of not one$:
-
$X_i$
$0$
$1$
total
$P$
$q$
$p$
1
- $E(X_i)=0・q+1・p$
- $V(X_i)=E(X_i^2)-E(X_i)^2=0^2・q+1^2・p-p^2=p(1-p)=pq$
$E(X)=\displaystyle\sum_{i=1}^4E(X_i)=4p$
$V(X)=\displaystyle\sum_{i=1}^4E(X_i)=4pq$
- Distribution of a random derivative is binominal distribution $B(n, p):$
- $E(X)=np, \; V(X)=npq,\; (p+q=1)$
- ¶ When casting a die 10 times, the probability of pip of one $p_x$
- $p_x=\binom{10}{x}p^xq^(10-x)=\frac{10!}{x!(10-x)!}\frac{5^{10-x}}{6^{10}}$
- 確率変数: random/ aleatory/ stochasitic variable
- 確率分布: probability distribution
- 期待値: expected value
- 不良品: defective good
- 最短経路: shortest path
- 重複組合わせ: repeated/ homogenerous combination
- 多項定理: polynominal theorem
- 係数: coefficient
- 偏差/分散: variance
- 標準偏差: standard
deviation
- 偏差値: standard score
- 標準測度: standard measure
- 二項分布: Binomial distribution
>Top
42. 正規分布
a
42. Normarl distribution:
- Binomianl distribution:
probability of event $a$ is $p$, and that of complementry event $q=1-p,\; P(X=r)$ is expressed as:
- $P(X=r)=\binom{n}{r}p^rq^{n-r}, \; (r=0,1,2, ...,n; \; p+q=1)$
- Expectation: $E(X)=\displaystyle\sum_{i=1}^nx_ipi=x_1p_1+x_2p_2+...+x_np_n$
- Variance: $V(X)=\displaystyle\sum_{i=1}^n(x_i-m)^2p_i$
$=\sum X_i^2p_i-2m\sum x_ip_i+m^2\sum p_i=E(X^2)-m^2$
, where $(\sum x_i^2p_i=E(X^2),\; \sum x_ip_i=E(X)=m,\; \sum p_i=1)$
- <Fig.1> Standard Deviation (SD), $\sigma{(X)}$:
- $\sigma{(X)}=\sqrt{V(X)}$
- 事象: event
- 余事象: complementary event
<Fig.1> Normal distribution:
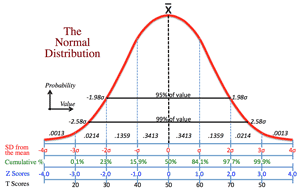
>Top
43. 統計的推測
a
43. Statistical estimation:
- <Fig.1> Continuous random variables:
- <Fig.2>
Where $f(x)\ge 0\; (\alpha\le x\le\beta), \; \int_{\alpha}^{\beta}f(x)dx=1$
Probability $P(a\le x\le b=\int_a^bf(x)dx$
- Average: $E(X)=\int_{\alpha}^{\beta}xf(x)dx$
- Variance: $V(X)=\int_{\alpha}^{\beta}(x-m)^2f(x)dx
=\int_{\alpha}^{\beta}x^2f(x)dx-m^2=E(X^2)-\{E(X)\}^2$
- SD: $\sigma(X)=\sqrt{V(X)}$
- Normal distribution: $X$ complies with normal distiriution $N(m, \sigma^2)$
- $f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-m)^2}{2\sigma^2}}$
- Average: $E(X)=m\;$, SD: $\sigma(X)=\sigma$
- Standardized random derivative: $Z=\frac{X-m}{\sigma}$
- Standard normal distribution: probability density function $\phi(x)$:
$\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$
- (University) deviation value: $Z=\frac{x-50}{10}$
- Approximation of binomial normal distribution:
- Where binominal distribution $B(n,p)$; a random derivative $X$, with sufficiently lart $n$; then
$Z=\frac{X-np}{\sqrt{npq}}$ follows the standard normal distribution $N(0,1)\;;(p+q=1)$
- ¶ casting a die 360 times; find the probability of pip of one which occurs no less thatn 55 times.
$X$ follows the binomial distribution
- 偏差値: deviation value
<Fig.1> Continuoius random variables:
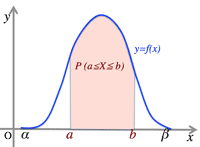
>Top
44. 双曲線関数
双曲線関数は三角関数によく似た関係式が成り立つ。
44. Hyperbolic function:
- $\cosh x=\frac{e^x+e^{-x}}{2}$
- $\sinh x=\frac{e^x-e^{-x}}{2}$
- $\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
- Inverse function of $y=\sinh x$ is:\; $y=\log{(x+\sqrt{x^2+1})}$
- Inverse function of $y=\cosh x$ is:\; $y=\log{(x\pm\sqrt{x^2-1})}$
Trigonometric
Hyperbolic
$e^x=\cosh x+\sinh x$
$e^{-x}=\cosh x-\sinh x$
$\cos^2x+\sin^2x=1$
$\cosh^2x-\sinh^2x=1$
$\tan x=\frac{\sin x}{\cos x}$
$\tanh x=\frac{\sinh x}{\cosh x}$
$1+\tan^2x=\frac{1}{\cos^2x}$
$1-\tanh^2x=\frac{1}{\cosh^2x}$
$\frac{1}{\tan^2x}+1=\frac{a}{\sin^2x}$
$\frac{1}{\tanh^2x}-1=\frac{a}{\sinh^2x}$
$(\sin x)'=\cos x$
$(\sinh x)'=\cosh x$
$(\cos x)'=-\sin x$
$(\cosh x)'=\sinh x$
$(\tan x)'=1+\tan^2x=\sec^2x$
$(\tanh x)'=1-\tanh^2x=sech^{2} x$
$(\cot x)'=-csc^2x=-\frac{1}{\sin^2x}$
$(\coth x)'=-csch^2 x=-\frac{1}{\sinh^2x}$
- $\cosh^2x+\sinh^2x=\cosh 2x$
- 確率密度関数: probability density function
<Fig.1> Hyperbolic functions
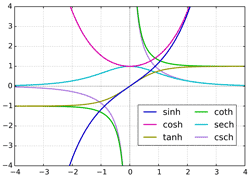
>Top
45. 線形代数
- Linearity satisfies additivity & homogeneity:
- $f(x+y)=f(x)+f(y)$
- $f(ax)=af(x)$
- Difference product: number is ${}_nC_2$
- $\Delta(x_1,\dots,x_n)=\prod_{i<j}(x_i-x_j)$
- $\Delta(x_1, x_2)=(x_1-x_2)$
- $\Delta(x_1, x_2, x_3)=(x_1-x_2)(x_1-x_3)(x_2-x_3)$
- $\Delta(x_1, x_2, x_3, x_4)=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_2-x_3)(x_2-x_4)(x_3-x_4)$
- Interchange:
- $\sigma=\dbinom{1 2 3 4 }{1 4 3 2}$
- $\Delta(x_{\sigma(1)},x_{\sigma(2)},x_{\sigma(3)},x_{\sigma(4)})
=(x_1,x_4,x_3,x_2)=-(x_1,x_2,x_3,x_4)$
- det A: $=\pmatrix{a_{11}&a_{12}&a_{13}\cr a_{21}&a_{22}&a_{23}\cr a_{31}&a_{32}&a_{33}}$
$=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}$
- linearity: 線形性
- non-linearity: 非線形性
- additivity: 加法性
- homogeneit: 斉次性
- determinant: 行列式hánglièshì
- difference producr: 差積
- permutation: 置換, 順列
>Top
46. xxxxxx
>Top
47. xxxxx
Comment
- a
- a
Mathematics Review (II/B/III/C)
|
Cat: SCI |
|
Compiled by Kanzo Kobayashi |
17214u/18403r |
Russian |
English |
Remarks |
|
0. 序文: |
0. Introduction: |
>Top 1. 整式と分数式:
|
1. Integral expression & Fractional expression:
|
|
||
|
|
|||
|
|
|||
>Top
2. 二次方程式:
|
2. Quadric equation:
|
|
>Top
3. 高次方程式:
|
3. High-degree equation
|
|
>Top
4. 恒等式と不等式:
|
4. Identity & Inequality:
|
|
>Top
5. 点と線:
|
5. Point & Line:
|
<Fig.1> Euler line |
>Top
6. 円:
|
6. Circle:
|
|
>Top
7. 軌跡と領域:
|
7. Locus & Domain:
|
|
>Top
8. 三角関数:
|
8. Trigonometric function:
|
|
>Top
9. 加法定理:
|
9. Trigonometric Addition Theorem:
|
<Fig.1> Addition theorem
|
||
オイラーの公式の活用 Euler's formula |
|
|||
>Top
10. 指数関数:
|
10. Exponential function:
|
|
>Top
11. 対数関数:
|
11. Logarithmic function:
|
|
>Top
12. 微分:
|
12. Differential calculus:
|
|
基本的な関数の
高次 |
$f(x)$ | $f'(x)$ | $f(x)$ | $f'(x)$ |
| $x^n$ | $nx^{n-1}$ | $\tan x$ | $sec^2 x$ | |
| $e^x$ | $e^x$ | $\cot x$ | $-csc^2 x$ | |
| $a^x$ | $a^x\log{a}$ | $\arcsin x$ | $\frac{1}{\sqrt{1-x^2}}$ | |
| $\log|x|$ | $\frac{1}{x}$ | $\arccos x$ | $-\frac{1}{\sqrt{1-x^2}}$ | |
| $\log_a|x|$ | $\frac{1}{x\log{a}}$ | $\arctan x$ | $\frac{1}{1+x^2}$ | |
| $\sin x$ | $\cos x$ | $\mathrm{arccot} x$ | $-\frac{1}{1+x^2}$ | |
| $\cos x$ | $-\sin x$ | |||
| $f(x)$ | $f^{(n)}$ | $f(x)$ | $f^{(n)}$ | |
| $x^\alpha$ | $\alpha(\alpha-1)...(\alpha-n+1)x^{\alpha-n}$ | $\sin x$ | $\sin(x+\frac{n\pi}{2})$ | |
| $e^x$ | $e^x$ | $\cos x$ | $\cos(x+\frac{n\pi}{2})$ | |
| $\log x$ | $(-1)^{n-1}\frac{(n-1)!}{x^n}$ | |||
| $(f\pm g)^{(n)}$ | $f^{(n)}\pm g^{(n)}$ | $(fg)^{(n)}=\displaystyle\sum_{k=0}^n\binom{n}{k}f^{(n-k)}g^{(k)}$ (Leibniz rule) | ||
| 積の 導関数 |
$(fg)'$ | $f'g+fg'$ | ||
| $(fg)'’$ | $f''g+2f'g'+fg''$ | |||
| $(fgh)'$ | $f'gh+fg'h+fgh'$ | |||
>Top
13. 導関数の応用:
|
13. Applicationed of derivative:
|
|
>Top
14. 積分:
|
14. Integral calculus:
|
|
>Top
15. <B> 数列:
|
15. Differential function:
|
|
||
Maclaurin series |
|
|||
Taylor series |
|
|||
>Top
16. 漸化式
|
16. Recurrence equation
|
|
>Top
17. 平面ベクトル
|
17. 2D vector
|
<Fig.1> ベクトルの減法: vector subtraction
|
>Top
18. ベクトルの応用
|
18. Application of vector:
|
<Fig.1> 位置ベクトル: position vector <Fig. 2> 内分点/外分点: internally/externally dividing point <Fig.3> 方向ベクトル: direction vector <Fig.4b> Vector equation on a circle:
|
|||||
<Fig.4> Circle:
|
<Fig.5> Triangle:
|
<Fig6> Parallelogram law:
|
<Fig.7> Orthocenter
|
<Fig.8> Isosceles:
|
|||
>Top
19. 空間ベクトル
|
19. 3D vector:
|
<Fig.1> 空間座標: spatial coordinates <Fig.2> Cube
|
>Top
20. 統計の基礎
|
20. Basic statistics:
|
|
>Top
21. コンピュータ・プログラム
|
21. Computer program:
|
>Top
22. <III> 関数
|
22. Function:
|
|
>Top
23. 数列の極限
|
23. Limit of sequence:
|
|
||
|
||||
>Top
24. 関数の極限
|
24. Limit of function::
|
<Fig.2> $\frac{\sin\theta}{\theta}$ |
||||
<Fig.1a> Exponential & logarithmic function: |
<Fig.1b> Exponential & logarithmic function: |
<Fig.3> Intermediate |
||||
>Top
25. 微分法
|
25. Differentiation:
|
|
>Top
26. いろいろな導関数
|
26. Various derivatives:
|
<Fig.1> シグモイド: sigmoid |
>Top
27. 関数の増減
|
27. Increase/decrease of function
|
<Fig.1> Mean value theorem:
|
>Top
28. 微分の応用
|
28. Application of differentiation:
|
|
||||
<Fig.1> Cycloid |
<Fig.2> Velocity |
<Fig.3> Uniform Circular Velocity |
<Fig.4> Approximation |
|||
>Top
29. 不定積分
|
29. Indefinite integral:
|
|
||||
|
|
|||||||||||||||||||||||||||||
>Top
30. 定積分
|
30. Definite integral:
|
Fig.1 $y=\sqrt{a^2-x^2}$
<Fig.2> Definite integral & Inequality:
|
||
|
<Fig.3 >Wallice's integrals: $W_0=\frac{\pi}{2},\;W_2=\frac{\pi}{4},\;W_4=\frac{3\pi}{16} ,\;W_6=\frac{5\pi}{32},\;W_8=\frac{35\pi}{56}...$ $W_1=1,\;W_3=\frac{2}{3},\;W_5=\frac{8}{15},\;W_7=\frac{16}{35}...$ |
>Top
31. 面積・体積
<Fig.6> Pyrmid: <Fig.7> Rotational body: |
31. Area and Volume:
|
<Fig.4> Area of Cycloid: <Fig.5> Volume by integral <Fig.8> Solid torus:
|
|||
<Fig.1> Area S1 |
<Fig.2> Area S2 |
<Fig.3> Area S3
|
|||
>Top
32. 高次導関数
|
32. Higher order derivative:
|
|
>Top
33. 平均値の定理・ロピタルの定理
|
33. Mean value theorem and L'Hôpital's rule:
|
|
>Top
34. 曲線の長さ
|
34. Length of curve:
|
<Fig.1> Length of curve: <Fig.2> Cycloid: <Fig.3> Asteroid: <Fig.4> Catenary:
|
||||
>Top
35. 微分方程式
|
35. Differential equation:
|
|
l >Top
36. <C> 行列
|
36. Determinant
|
|
||||
>Top
37. 行列の応用
|
37. Application of determinant
|
<Fig.1> Rotation around the origin: <Fig.2> Synthetic transformation: <Fig.3> Addtion theorem of trigonometry: |
>Top
39. 媒介変数・極座標
<Fig.9> Polar equation of quadratic: |
39. Parameter and polar coordinates:
|
<Fig.0> Ellipse <Fig.5> Lissajous curves: |
||||
<Fig.1> Cycloid |
<Fig.2> Asteroid |
<Fig.3> Cardioid |
<Fig.4> Logarithmic spiral |
|||
<Fig.6> Lemniscate |
<Fig.7> Involute curve |
<Fig.8> Folium of Decartes |
<Fig.11> $r=\cos3\theta$ |
|||
<Fig.10> $r=\sin n\theta (n=2, 3, 4, 5, 6, 7, 8)$     |
||||||
>Top
40. 条件付き確率
|
40. Conditional probability:
|
<Fig.0> Shortest path: |
|||||||||||||||||||
<Fig.1> A and B: |
<Fig.2>
|
||||||||||||||||||||
>Top
41. 確率分布
|
41. Probability distribution:
|
|
>Top
42. 正規分布
|
42. Normarl distribution:
|
<Fig.1> Normal distribution: |
>Top
43. 統計的推測
|
43. Statistical estimation:
|
<Fig.1> Continuoius random variables: |
>Top
44. 双曲線関数
|
44. Hyperbolic function:
|
<Fig.1> Hyperbolic functions |
||||||||||||||||||||||
>Top
45. 線形代数 |
|
|
||||||||||||||||||||||
>Top
46. xxxxxx |
||||||||||||||||||||||||
>Top
47. xxxxx |
Comment |
|
|