| Bottom | Home | Article | Bookshelf | Keyword | Author | Oxymoron |

 

Indian Calculation Method
Cat: SCI
Pub: 2019
#1916a

Compiled by K. Kobayashi
up 19z25
Title

Indian Caluclation Method

インド式計算方法
Index
  1. Additon: 19+37=20-1+40-3:
  2. Rule-1a: 123☓456:
  3. Rule-1b: 123☓46:
  4. Rule-1c: 12☓34:
  5. Rule-2a: 31☓37:
  6. Rule-2b: 11☓19:
  7. Rule-2c: 111☓119:
  8. Rule-2d: 15☓15:
  9. Rule-2e: 23☓83:
  10. Rule-2f: 11☓17:
  11. Rule-3: 19☓19:
  12. Rule-4a: 99☓101:
  13. Rule-4b: 34☓36:
  14. Rule-4c: 16☓51:
  15. Rule-5: 1/3/3/1:
  16. Rule-6a: 22☓5:
  17. Rule-6b: 36☓25:
  18. Rule-6c: 43☓11:
  19. Rule-7: 18☓99:
  1. 加算:
  2. たすき掛け: 3桁☓3桁:
  3. たすき掛け: 3桁☓2桁:
  4. たすき掛け: 2桁☓2桁:
  5. 十位数等しい場合:
  6. 十位数等しく&一位数和10:
  7. 十位数以上数等しく&一位数和10:
  8. 十位数等しく&一位数それぞれ5:
  9. 十位数和10で&一位数が等しい:
  10. 十位数1の計算:
  11. 11〜19の二乗公式:
  12. (a+b)(a-b)型:
  13. 0/5に寄せて計算:
  14. 片方を一位数0に寄せる:
  15. 三乗公式:
  16. 偶数☓5:
  17. 4倍数☓25:
  18. 11倍数の計算:
  19. 9連数の計算:
Guide
  • The Indian method calculation is useful, but seem a little tricky; which needs to select the best method depending on the cases.
  • Followings are various methods listed from general rule to specific rule.
  • Verification of the caluculation should be done by 'Casting Out Nine' method.
Original resume
Remarks

>Top 0. Addition:

  • Use nearest roundup figures:
    • 19+37=(20-1)+37=56
    • 88+96=(90-2)+(90+6)=184
    • 129+214=(100+200)+29+14=300+(30-1)+(10+4)= 343
    • 719+548=700+500+19+48=1267
    • 986+857=(1000+800)-14+57=1843

  • There are many spaces without having easier method of calculation. (>Fig.)

1916/indiancalculate      

>Top Rule-1a: Cross-multiplation: $(a+b)(c+d)=ac+ad+bc+bd$;

  • 384☓295=6|27+16|15+72+8|40+36|20=6|43|95|76|20=11|3|2|8|0=113280
    [|の両隣の和の一位数を記入。桁上りあり]
  • 467☓789=28|32+42|36+48+49|54+56|63=28|74|133|110|63=36|8|4|6|3

1. ３桁☓3桁: 上の桁から位数同士掛け算

  • abc☓xyz
    • 10000位数: ax
    • 1000位数: ay+bx
    • 100位数: az+by+cx
    • 10位数: bz+cy
    • 1位数: cz
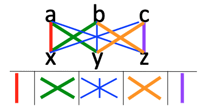
 33multiply

>Top Rule-1b: Cross-multiplation: $(a+b)(c+d)=ac+ad+bc+bd$;

  • 384☓29=6|27+16|72+8|36=6|43|80|36=11136
    [|の両隣の和の一位数を記入。桁上りあり]
  • 467☓78=28|32+42|48+49|56=28|74|97|56=36426
  • 789☓57=35|49+40|56+45|63=35|89|101|63=44973

2. ３桁☓2桁: 上の桁から位数同士掛け算

  • abc☓xy
    • 1000位数: ax
    • 100位数: ay+bx
    • 10位数: by+cx
    • 1位数: cy

>Top Rule-1c: Cross-multiplation: $(a+b)(c+d)=ac+ad+bc+bd$;

  • 23☓57=(20+3)(50+7)=20☓50+20☓7+3☓50+3☓7=1000+140+150+21=1000+290+21=1311
    or 10|15+14|21=1311
  • 76☓89=(70+6)(90-1)=6300+540-70-6=6300+440+24=6764
    or 56|63+48|54=6764
  • 31☓84=(30+1)(80+4)=2400+120+80+4=2604
    or 24|12+8|4=2604
  • 79☓51=(80-1)(50+1)=4000+80-50-1=4029
    or 35|7+45|9=4029

3. ２桁☓2桁: 上の桁から位数同士掛け算
（10位数の数=外☓外+内☓内, 切り上げあり得る）

  • ab☓xy
    • 100位数: ax
    • 10位数: ay+bx
    • 1位数: by

 

>Top Rule-2a: Cross-multiplation: $(10a+b)(10a+c)=10a(10a+b+c)+bc$;

  • 22☓24=(20+2)(20+4)=20☓20+20(2+4)+2☓4=20(20+6)+8=520+8=528
    or        = 20(22+4)+8=520+8=528
  • 31☓37=(30+1)(30+7)=30(30+8)+7=900+240+7=1147
  •  or      =30(31+7)+7=38･30+7=1147
  • 42☓45=(40+2)(40+5)=40(40+7)+10=1600+280+10=1890
  • or       =(42+5)40+10=94･20+10=1880+10=1890
  • 71☓78=(70+1)(70+8)=4900+630+8=5538
  •  or      =70(71+8)+8=70☓79+8=5538
  • 83☓85=80(83+5)+15=80☓88+15=7040+15=7055
  • 93☓97=9021 (<Rule-10)
  •  or      = 90(93+7)+21=9021

4. たすき掛け(十位数等しい場合):

  • (10a+b)(10a+c)=10a☓10a+10a(b+c)+bc
    =10a(10a+b+c)+bc; b+c=10
    =100a(a+1)+bc
  • 十位数(1項目+2項目の一位数)+一位数同士掛け算

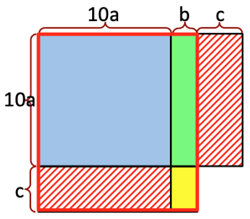
rule_2

>Top Rule-2b: (10a+b)(10a+c); b+c=10

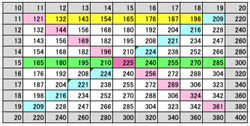
  • 11☓19=209; 12☓18=216; 13☓17=221; 14☓16=224; 15☓150=225
  • 21☓29=609; 22☓28=616; 23☓27=621; 24☓26=624; 25☓25=625
  • 31☓39=1209; 32☓38=1216; 33☓37=1221; 34☓36=1224; 35☓35=1225
  • 41☓49=2009; 42☓48=2016; 43☓47=2021; 44☓46=2024; 45☓45=2025
  • 51☓59=3009; 52☓58=3016; 53☓57=3021; 54☓56=3024; 55☓55=3025
  • 61☓69=4209; 62☓68=4216; 63☓67=4221; 64☓66=4224; 65☓65=4225
  • 71☓79=5609; 72☓78=5616; 73☓77=5621; 74☓76=5624; 75☓75=5625
  • 81☓89=7209; 82☓88=7216; 83☓87=7221; 84☓86=7224; 85☓85=7225
  • 91☓99=9009;92☓98=9016; 93☓97=9021; 94☓96=9024; 95☓95=9025

5. 十位数等しく&一位数和10の場合:
(どちらかの十位数とそれに+1した数とを掛けて100倍、後は一位数の積を足す)★1

  • (10a+b)(10a+c)=10a☓10a+10a(b+c)+ab
    =10a(10a+b+c)+bc=100a(a+1)+bc

>Top Rule-2c: (100a+10b+c)(100a+10b+d); c+d=10

  • 111☓119=13209; 112☓118=13216; 113☓117=13221; 114☓116=13224; 115☓115=13225
  • 121☓129=15609; 122☓128=15616; 123☓127=15621; 124☓126=15624; 125☓125=15625
  • 131☓139=18209; 132☓138=18216; 133☓137=18221; 134☓136=18224; 135☓135=18225
  • 141☓149=21009; 142☓148=21016; 143☓147=21021; 144☓146=21024; 145☓145=21025
  • 151☓159=24009; 152☓158=24016; 153☓157=24021; 154☓156=24024; 155☓155=24025
  • 161☓169=27209; 162☓168=27216; 163☓167=27221; 164☓166=27224; 165☓165=27225
  • 171☓179=30609; 172☓178=30616; 173☓177=30621; 174☓176=30624; 175☓175=30625
  • 181☓189=34209; 182☓188=34216; 183☓187=34221; 184☓186=34224; 185☓185=34225
  • 191☓199=38009; 192☓198=38016; 193☓197=38021; 194☓196=38024; 195☓195=38025
  • 991☓999=990009; 992☓998=990016; 993☓997=990021; 994☓996=990024; 995☓995=990025

6. 十位数以上数等しく&一位数和10の場合: ★

  • (100a+10b+c)(100a+10b+d)
    =$(100a+10b)^2+(100a+10b)(c+d)+cd$
    = 100(10a+b)(10a+b+1)+cd

>Top Rule-2d: $(10a+5)^2=(10a)^2+10^2a+25=10^2a(a+1)+25$:

  • 15☓15=225; 25☓25=625; 35☓35=1225; 45☓45=2025; 55☓55=3025; 65☓65=4225; 75☓75=5625; 85☓85=7225; 95☓95=9025
  • 145☓145=(140+5)(140+5)=140(140+10)+25=14☓15☓100+25=21025
  • 1005☓1005=(1000+5)(1000+5)=1000(1000+10)+25=1010025

7. 十位数が等しく&一位数がそれぞれ5の場合 (簡単)
(十位数と十位数+1を掛けて、後は残り一位数の積を足す)

>Top Rule-2e: (10a+c)(10b+c); a+b=10

  • 11☓91=1001; 12☓92=1104; 13☓93=1209; 14☓94=1316; 15☓95=1425; 16☓96=1536;
    17☓97=1649; 18☓98=1764; 19☓99=1881
  • 21☓81=1701; 22☓82=1804; 23☓83=1909; 24☓84=2016; 25☓85=2125; 26☓86=2236;
    27☓87=2349; 28☓88=2464; 29☓89=2581
  • 31☓71=2201; 32☓72=2304; 33☓73=2409; 34☓74=2516; 35☓75=2625; 36☓76=2736;
    37☓77=2849; 38☓78=2964; 39☓79=3081
  • 41☓61=2501; 42☓62=2604; 43☓63=2709; 44☓64=2816; 45☓65=2925; 46☓66=3036;
    47☓67=3149; 48☓68=3264; 49☓69=3381
  • 14☓94
    • 1☓9+4=13
    • 4☓4=16
    • 1300+16=1316

8. 十位数和10で&一位数等しい場合:
(十位数同士掛け算してどちらかの一位数を加えて100倍、後は残りの一位数の積を足す) ★★

  • (10a+c)(10b+c)=100ab+10c(a+b)+$c^2$
    =100(ab+c)+$c^2$

>Top Rule-2f: (10+a)(10+b)=100+10(a+b)+ab:

  • 11☓11=121; 11☓12=132; 11☓13=143; 11☓14=154; 11☓15=165; 11☓16=176
  • 12☓12=144; 12☓13=156; 12☓15=17'0; 12☓17=19'4; 12☓19=21'8
  • 13☓13=169; 13☓14=17'2; 13☓15=18'5; 13☓17=20''1; 13☓19=22''7
  • 14☓14=18'6; 14☓15=19''0; 14☓17=21''8; 14☓19=23'''6=266
  • 16☓16=22'''6; 16☓17=230+42=272; 16☓19=250+54=304;
  • 17☓17=240+49=289; 17☓18=250+56=306; 17☓19=260+63=323;
  • 18☓18=260+64=324; 18☓19=270+72=342; 19☓19=28+81=361

9. 十位数1の二桁計算:
(10＋一位数の足し算)を10倍＋一位数同士掛け算) ★(桁上りありTricky)

  • (10+a)(10+b)
    =10{(10+(a+b)}+ab

>Top Rule-3: $(10a+5)^2=(10a)^2+10^2a+25=10^2a(a+1)+25$:

  • 11☓11=121; 12☓12=144; 13☓13=169; 14☓14=1(8+1)6=196; 15☓15=225; 16☓16=1+1|2+3|6=256; 17☓17=1+1|4+4|9=289; 18☓18=1+1|6+6|4=324; 19☓19=1+1|8+8|1=361
  • 21☓21=441; 22☓22=484; 23☓23=4+1|2|9=529; 24☓24=4+1|6+1|6=576; 25☓25=625; 26☓26=4+2|4+3|6=676; 27☓27=4+2|8+4|9=729; 28☓28=4+3|2+6|4=784; 29☓29=4+3|6+8|1=841
  • 31☓31=961; 32☓32=9+1|2|4=1024; 33☓33☓=9+1|8|9=1089; 34☓34=9+2|4+1|6=1156; 35☓35=1225; 36☓36=9+3|6+3|6=1296; 37☓37=9+4|2+4|9=1369; 38☓38=9+4|8+6|4=1444; 39☓39=9+5|4+8|1=1521
  • 41☓41=1681; 42☓42=16+1|6|4=1764; 43☓43=16+2|4|9=1849; 44☓44=16+3|2+1|6=1936; 45☓45=2025; 46☓46=16+4|8+3|6=2116; 47☓47=16+5|6+4|9=2209; 48☓48=16+6|4+6|4=2304; 49☓49=16+7|2+8|1=2401
  • 51☓51=25+1|0|1=2601; 52☓52=25+2|0|4=2704; 53☓53=25+3|0|09=2809; 54☓54=25+4|0+1|6=2916; 55☓55=25+5|0+2|5=3025; 56☓56=25+6|0+3|6=3136; 57☓57=25+7|0+4|9=3249; 58☓58=25+8|0+6|4=3364; 59☓59=25+9|0+8|1=3481;
    or 59☓59=5☓5+9|+81=3481 (<Rule-11)
  • 素数>素数: 17☓17=289; 23☓23=529; 29☓29=841; 31☓31=961

10. 11〜19二乗公式は先ず覚える!:
(中間項は一位数の2倍/4倍/6倍...、桁上りあり)

  • 1|21,44,69,96; 2|25,56,89; 3|24,61
  • 4|41,84; 5|29,76; 6|25,76; 7|29,84; 8|41
  • 9|61; 10|24,89; 11|56; 12|25,96; 13|69; 14|44; 15|21
  • 下2桁に頻度特徴: 14数, 内素数4個21,24,25,29,36,41,44,
    56,61,69,76,84,89,96
  • 下1桁は、1,4,9,6,5,6,9,4,1の繰り返し

>Top Rule-4a: $(a+b)(a-b)=a^2-b^2$:

  • 99☓101=(100-1)(100+1)=10000-1=9999
  • 78☓82=(80-2)(80+2)=6400-4=6396
  • 994☓1006=(1000-6)(1000+6)=1000000-36=999964

11. $a^2-b^2$形: 丸いaにする

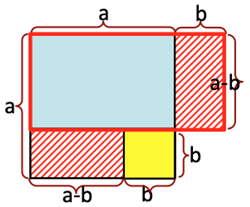
rule_3

>Top Rule-4b: $a^2=(a+b)(a-b)+b^2$:

  • 一位数が1, 6の場合:
    • 36☓36=(35+1)(35+1)=35☓35+2☓35+1=1225+71=1296
    • 41☓41=(40+1)(40+1)=40☓40+2☓40+1=1600+81=1681
  • 一位数が4, 9の場合:
    • 34☓34=(35-1)(35-1)=35☓35-2☓35+1=1225-70+1=1155+1=1156
    • 79☓79=(80-1)(80-1)=80☓80-2☓80+1=6400-160+1=6241
  • その他:
    • 17☓17=(15+2)(15+2)=15☓15+4☓15+4=225+60+4=289
    • 28☓28=(25+3)(25+3)=25☓25+6☓25+9=625+150+9=784
    • 43☓43=(45-2)(45-2)=45☓45-4☓45+4=2025-180+4=1845+4=1849
    • 996☓996=(1000-4)(1000-4)=1000☓1000-8☓1000+16=992016

12. 0か5の一位数に寄せて計算:
特に、一位数が1, 6または4, 9の場合は楽                                               　   

>Top Rule-4c: $a(b+c)=ab+ac$:

  • 16☓51=16(50+1)=8☓100+16=816
  • 49☓23=(50-1)(20+3)=1000+150-20-3=1150-23=1127
  • 127☓998=(130-3)(1000-2)=130000-3000-260+6=126746

13. 片方を(一位数0の)丸い数字にして計算:

>Top Rule-5: $(a+b)^3=a^3+3a^2+3ab^2+b^3$:

  • $12^3=(10+2)^3=10^3+3･10^2･2+3･10･2^2+2^3$
    =1000+3☓100☓2+3☓10☓4+8
    =1000+600+120+8=1728
  • $61^3=(60+1)^3$
    = 216000+3☓3600☓1+3☓1☓60+1
    =216000+10800+180+1=226981
    or=$216+3･216\frac{1}{6}+3･216(\frac{1}{6})^2+1$
    =216|3☓36|3☓6|1=216|108|18|1=226|9|8|1=113491
  • $39^3$=27|3☓9☓9|3☓3☓81|729=27|243|729|729=59|3|1|9=59319

14. 三乗公式:

  • $(a+b)^3=a^3+3a^2b+3ab^2+b^3$
  • =$a^3+a^2b+ab^2+b^3$
       +    $2a^2b+2ab^2$
    ---------------------------
  • =$a^3+3a^3 \frac{b}{a}+3a^3(\frac{b}{a})^2+a^3(\frac{b}{a})^3$

>Top Rule-6a: 2n☓5:

  • 22☓5=110; 26☓5=130; 36=5☓180; 38☓5=190; 46☓5=230; 76☓5=380; 96☓5=480; 98☓5=490
  • 28☓5
    • 28☓10/2=14☓10
      =140

15. 偶数☓5の積算:

  • $2n☓5=2n☓\frac{10}{2}=10n$

>Top Rule-6b: 4n☓25:

  • 12☓25=3☓100=300; 16☓25=4☓100=400; 24☓25=6☓100=600; 28☓25=700; 32☓25=800; 36☓25=900; 44☓25=1100; 48☓25=1200; 52☓25=1300; 56☓25=1400; 64☓25=1600; 68☓25=1700; 72☓25=1800; 76☓25=1900; 84☓25=2100; 88☓25=2200; 92☓25=2300; 96☓25=2400;
  • 528☓25=4☓132☓100/4=13200
  • 992☓25=24800; 996☓25=24900

16. ４倍数☓25

  • $4n☓25=4n☓\frac{100}{4}=n☓100$

>Top Rule-6c: (10a+b)☓11:

  • 43☓11=4|4+3|3=473; 97☓11=9|9+7|7=1067
  • 12☓11=132; 13☓11=143; 14☓11=154; 15☓11=165; 16☓11=176; 17☓11=187; 18☓11=198;
    19☓11=209; 21☓11=231; 22☓11=242; 23☓11=253; 24☓11=264; 25☓11=275; 26☓11=286;
    27☓11=297; 28☓11=308; 29☓11=319; 31☓11=341; 32☓11=351; 33☓11=363; 34☓11=374
  • 26☓11
    • 2+6=8
    • 200+80+6=286
  • 139☓11=1|4|12|9=1529
  • 234567☓11=2|5|7|9|11|13|7 =2580237

17. 11倍数の積算: ★
(3桁☓11の場合は、一位数はそのまま、十位数=十位+一位、百位数＝百位+十位として並べる。以下同様(桁上りあり。）

  • (100a+10b+c)11=(100a+10b+c)(10+1)
    =1000a+100(a+b)+10(b+c)

>Top Rule-7: (10a+b)99: (10a+b)≤99

  • 18☓99=17(100-1)+100-1=1700+(100-18)=1782; 19☓99=1881; 23☓99=2277; 29☓99=2871;
    31☓99=3069
  • 37☓999=36(1000-1)+1000-1=36000+(1000-037)=36963
  • 67☓9999=66(10000-1)+10000-1=660000+(10000-0067)=669933
  • 89☓99999=88(100000-1)+100000-1=8800000+(100000-00089)=8899911
  • 990☓9999=989(10000-1)+10000-1=9890000+(10000-0990)=9899010

18. ９連数の積算: ★

  • tens' compliment: 100-37=3̄7̄=63
Comment
  • It is widely said that Indian pupils learns 2-digts table calculation; Indian calculation method is said to be smart and essential, but there are too many rules to learn, which looks not smart.
  • The above rules through rule-7 are general rules; the others could be used case by case.
  • インドの生徒は二桁の九九 (19-19)を学んでいると言われている。インド式計算方法はスマートで本質的と言われているが学ぶのには多くの規則があり、それはスマートとは言えない。
  • 上記の7番目迄の規則は一般的だが、他は状況次第で利用する。
 
  • >Top <Casting Out Nine> *complimentary*
  • Adding the decimal digit of a number, while ignoring 9s or digits which sum multple of 9. (casting out 9s)
  • Repeating this procedure until a single-digit number is obtained. (digital root: 9 or the remainder after divded by 9)
  • any sanity-test is used to check arithmetical calculations.
  • <九去法> *おまけ*
  • 9または合計9になる数字は除去する。
  • 各数値が１桁になるまで繰り返して、数字根を求める
  • 元の計算と求めた数字との数字根が一致すれば検算終わり

| Top | Home | Article | Bookshelf | Keyword | Author | Oxymoron |