$\boxed{e^{\int p(x)dx}}$
Memorandum of Differential Equations
Cat: SCI
Pub: 2020
#2009
compiled by Kanzo Kobayashi from various sources
20606u
Title
Memorandum of Differential Equations
微分方程式メモ
Index
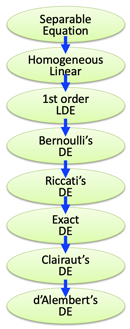
- Summary:
- Separable equations:
- Homogeneous function:
- First-order linear differential equation:
- J. Bernoulli's differential equation:
- Y. Riccati's differential equation:
- Exact differential equation:
- Exact differential equation (II):
- A. Clairaut's differential equation:
- d'Alembert's (Lagrange's) DE:
- Second-order LDE & Wronskian:
- Constant coefficient second-order linear homogeneous DE (I):
- Constant coefficient second-order linear homogeneous DE (II):
- Constant coefficient second-order linear nonhomogeneous DE (I):
- Constant coefficient second-order linear nonhomogeneous DE (II):
- Euler's DE (I):
- Euler's DE (II)
- Euler's DE (III):
- Differential operator:
- Solution by differential operator:
- Series expansion:
Tag
; ; ; Bernoulli DE; Differential formula; Differential operator; Euler's formula; Exact DE; First-order LDE; ; Homogeneous function; Integral formula; LDE; Partial integration; Riccati DE; Second-order LDE; Separable equation; Simply connected area; Wronskian; ;
Why
- History of mathematics of differential equations (DE) appears around 1670, which corresponds to the start of modern history.
- In senior high schools, basic calculus and differential starts (why such is an elective subject!), and in university DE starts (as one of selective scientific subjects).
- The knowledge of DE helps us to understand clearly any type changes or relationship between the two expressed by such as alteration, variation, variance, fluctuation, velocity, growth, decay, shift, rotation, and derivative, etc.
- It is interesting DE has solvable solutions in some forms, but in solvable in most cases; which may corresponds that we can know something but cannot most of things.
- The method of DE is really 'standing on the shoulders of giants'; not only Newton & Leibniz, and academic mathematical books, but also many easy to learn online programs.
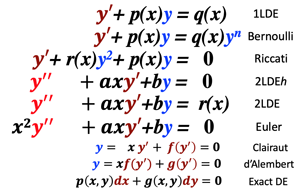
Name of DE
Format of DE
Formula Summary
>Top
変数分離型
Separable eq
$y'=f(x)g(y)$
0. Formula:
- $\int \frac{1}{g(y)}dy=\int f(x)dx$
同次形
$y'=f(\frac{y}{x})$
- homogeneous: $f(kx,ky)=k^nf(x,y)$
- let: $u(x)=\frac{y}{x}$
- $\int \frac{1}{f(u)-u}du=\int \frac{1}{x}dx$
1-LDE
$y'+p(x)y=q(x)$
- assume: $y=C(x)e^{-\int p(x)dx}$ [VC]
- multiply: $e^{-\int p(x)dx}$ [IF]
- $y=e^{-\int p(x)dx}(\int q(x)e^{\int p(x)dx}dx+C)$
Bernoulli DE
$y'+p(x)y=q(x)y^n$
- divide by: $y^n$
- let: $u=y^{1-n}$
- $u'+'1-n)p(x)u=(1-n)q(x)$ [1LDE]
Riccati DE
$y'+r(x)y^2+p(x)y=q(x)$
- let: $y=y_1+u$
- $u'+s(x)u=-r(x)u^2$ [Bernoulli DE]
Exact DE
$p(x,y)dx+q(x,y)dy=0$
- $df(x,y)=\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy
=p(x,y)dx+q(x,y)dy=0$
- $df(x,y)=0→ f(x,y)=C$
- $f(x,y)=\int p(x,y)dx+\int\left(q(x,y)
-\frac{\partial}{\partial y}\int p(x,y)dx\right)dy,\;
f(x,y)=C$
Clairaut DE
$y=xy'+f(y')=0$
- 1) $y''=0→\; y=Cx-C^2=0$
- 2) $x=-f'(y')0,\; y=-f'(y')y'+f(y')$ [eliminate $y'$ or parameterise]
d'Alembert DE
$y=xf(y')+g(y')=0$
- 1) $y=xf(p)+g(p)$
- 2)$x=e-\int P_0(p)dp(\int q_0(p)^{\int P_0dp}dp+C)$
C-2-LDE (homo ass.eq)
$y''+ay'+by=0$
- assume: $y=e^{\lambda x}$ [either FS]
- $y=C_1y_1+C_2y_2$ [GS]
- here: $\lambda^2+a\lambda+b=0$ [characteristic eq]
- D>0: $y_ 1=e^{\lambda_1x},\;y_2=e^{\lambda_2x}
→\;y=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}$ [GS]
- D=0: $y_1=e^{\lambda_1x},\;\mathrm{assume:} y_2=xe^{\lambda_1x}
→\;y=C_1e^{\lambda_1x}+C_2xe^{\lambda_1x}$ [GS]
- D<0: $y_ 1=e^{\lambda_1x},\;y_2=e^{\lambda_2x},
\; \lambda_1=\alpha+u\beta,\; \lambda_2=\alpha-u\beta$
$→\;y=C_1e^{\lambda_1x}+C_2xe^{\lambda_1x}
=C_1e^{\alpha x}e^{i\beta x}+C_2e^{\alpha x}e^{-i\beta x}
→\;y=e^{\alpha x}(C_3\cos\beta x+C_4\sin\beta x)$ [GS]
C-2-LDE (nonhomo)
$y''+ay'+by=r(x)$
- y=y_0+Y→\;y_0+C_1y_1+C_2y_2: [GS=SS+GS0]
- assume: $y_0=C_1(x)y_1+C_2(x)y_2$
- find solution ($C_1(x),\;C_2(x)$) of $C_1'(x)y_1+C_2'(x)y_2=0$
- $→\;y_0=-y_1\int\frac{y_2r(x)}{W(y_1,y_2)}dx+y_2\int\frac{y_1r(x)}{W(y_1,y_2)}dx$
- $y=C_1y_1+C_2y_2
-y_1\int\frac{y_2r(x)}{W(y_1,y_2)}dx+y_2\int\frac{y_1r(x)}{W(y_1,y_2)}dx$
C-2-LDE
(nonhomo) w.
1 GS0 only
$y''+ay'+by=r(x)$
- assume $y=u(x)y_1$
- let: $u'(x)=p→\;p'+P_0(x)p=Q_0(x)$ [1LDE]
- $p=e^{-\int P_0(x)dx}(\int Q_0(x)e^{\int P_0(x)dx}dx+C_1)$
- $u'(x)=p,\; y=u(x)y_1$ [GS]
Euler DE
$x^2y''+axy'+by=0$
- assume: $y=x^{\lambda}$ [FS]
- here: $\lambda^2+(a-1)\lambda+b=0$ [characteristic eq]
- D>0: $y_ 1=x^{\lambda_1},\;y_2=x^{\lambda_2}
→\;y=C_1x^{\lambda_1}+C_2x{\lambda_2}$
- D=0: $y_1=x^{\lambda_1},\;\mathrm{assume:} y_2=u(x)x^{\lambda_1}
let: $u'(x)=p→\;
u(x)=C_3\log x+C_4=\log x→\;y_2=x^{\lambda_1}\log x
→\;y=C_1x^{\lambda_1}+C_2x^{\lambda_1}\log x
- D<0: $y_ 1=x^{\lambda_1},\;y_2=x^{\lambda_2}
here: \lambda_1=\alpha+i\beta,\;\lambda_2=\alpha^i\beta$
$→\;y_1=x^{\alpha}\bigl(\cos(\beta\log x)+i\sin(\beta\log x)\bigr)$
$,\; y_2=x^{\alpha}\bigl(\cos(\beta\log x)-i\sin(\beta\log x)\bigr)$
$\therefore\; y=x^{\alpha}\bigl(C_1\cos (\beta\log x)+C_2\sin (\beta\log x)\bigr)$
- let newly $y_1=\frac{1}{2}(x^{\lambda_1}+x^{\lambda_2})
=x^{\alpha}\cos(\beta\log x),$
$y_2=\frac{1}{2}(x^{\lambda_1}-x^{\lambda_2})
=x^{\alpha}\sin(\beta\log x)$
$y=C_1x^{\alpha}\cos (\beta\log x)+C_2x^{\alpha}\sin (\beta\log x)$
Euler DE (II)
$x^2y''+axy'+by=0$
- let: $x=e^t→\;t=\log x$
$→\;\frac{d^2}{dt^2}+(a-1)\frac{dy}{dt}+by=0$...(**)
- assume: $y=e^{\lambda t}$
$→\;\lambda^2+(a-1)\lambda+b=0$...(*3) [char.eq]
- D>0: let: $y_1=e^{\lambda_1 t},\; y_2=e^{\lambda_2 t}
→\;y=C_1x^{\lambda_1}+C_2x^{\lambda_2}$
- D=0: let: $y_1=e^{\lambda_1 t},\; y_2=te^{\lambda_2 t}
→\;y=C_1x^{\lambda_1}+C_2x^{\lambda_1}\log x$
- D<0: let: $y_1=e^{\lambda_1 t},\; y_2=te^{\lambda_2 t}$
here: $\lambda_1=\alpha+i\beta,\;\lambda_2=\alpha-i\beta$
$→\;y_1=x^{\alpha}\cos (\beta\log x),\;
y_2=x^{\alpha}\sin (\beta\log x)$
$
→\;y=C_1x^{\lambda_1}+C_2x^{\lambda_1}\log x$
- $→\;y=C_1x^{\alpha}\cos(\beta\log x)+C_2x^{\alpha}\sin(\beta\log x)$
Original resume
Remarks
>Top 1. Separable equation:
-
$\frac{dy}{dx}=f(x)g(y)$
- when $g(y)≠ 0$
$\frac{1}{g(y)}\frac{dy}{dx}=f(x)$
$\int\frac{1}{g(y)}\frac{dy}{dx}dx=\int f(x)dx$
$\therefore\int\frac{1}{g(y)}dy=\int f(x)dx\;$ [Integration by substitution]
- ¶ 1: Solve: $y'=2xy \;$ where, $y(0)=1$ [initial condition]
- $\frac{dy}{dx}=2xy$ ... (*)
- $y=o$ is the solution of the above (*). [special solution=SS]
- when $y≠ 0, \;→ \int\frac{1}{y}dy=\int 2xdx$
- $\log|y|=x^2+C \ \;→ |y|=e^{x^2}+C$
- $y=± e^ce^{x^2}=C'e^{x^2} \;(C'=± e^c)$ ...(**)
- $y=0$, then $C'=0$
- $\therefore y=Ce^{x^2}\; $(C: aribitray constant; general solution=GS)■
- ¶2: Solve: $y'=1-y^2$
- $\frac{dy}{dx}=(1-y)(1+y)$ ...(*)
- $y=1, -1$ are solution of above (*)
- when $y≠ 1, \;\int\frac{1}{(1-y)(1+y)}dy=\int dx$
- $\frac{1}{2}\log|\frac{1+y}{1-y}|=x+C$
- $|\frac{1+y}{1-y}|=e^{2x+2C}=C'e^{2x}\; (C'=± e^{2C})$
- $y=\frac{C'e^{2x}-1}{C'e^{2x}+1}$ ...(**)
- $y=-1$ is solutions when $C'=0$, and $y=1$ is also solution when $C'=\infty$
- then $y=\frac{Ce^{2x}-1}{Ce^{2x}+1}\;$ [GS]■
- ¶3: Solve: $(x+1)y'+(y+1)=0$
- $(x+1)dy+(y+1)dx=0$
$\frac{1}{y+1}dy=-\frac{1}{x+1}dx$
$\int\frac{1}{y+1}dy=\int-\frac{1}{x+1}dx$
$\log|y+1|=-\log|x+1|+C \;→y+1=±\frac{1}{e^C(x+1)}$
$\therefore y=\frac{C}{x+1}-1$
- $y=(0)=2 \;→2=C-1 \therefore y=\frac{3}{x+1}-1$■
- ¶4: $v'=a$ [equation of motion; v=velocity, a=acceleration]
- $→\;v=\int adt=at+C=at+v_0\;$, where [$t=o, v=v_0$ initial velocity]
- $→\;v=\frac{dx}{dt}=at+v_0$
$→\;x=\int (at+v_0)dt=\frac{1}{2}at^2+v_0t+C_2)\;$ [$t=0, x=x_0$]
$→\;x=\frac{1}{2}at^2+v_0t+x_0$
- ¶5: $m\frac{dv}{dt}=mg-kv\;$
[separable DE; v=velocity, t=time, m/g/k=constant; m=mass, g=gravity, k=air resistance]
- $\frac{m}{mg-kv}\frac{dv}{dt}=1$
- $\int\frac{1}{mg-kv}dv=\frac{1}{m}\int dt$
→$ -\frac{1}{k}\log|mg-kv|=\frac{t}{m}+C$
→$\log|mg-kv|=-\frac{kt}{m}+C$
- here $v(0)=0\;→C=\log{mg}$
- $mg-kv=e^{-\frac{kt}{m}+C}\;→kv=mg-e^{-\frac{kt}{m}+\log{mg}}
=mg(1-e^{\frac{kt}{m}})$
$\therefore v=\frac{mg}{k}(1-e{\frac{kt}{m}})$■
1. 変数分離型:
- integration by substitution: 置換積分
- arbitrary constant: 任意定数
- particulr solution: 特殊解
- general solution: 一般解
- Step of solutions of LDE:
>Top 2. Homogeneous function:
-
$\frac{dy}{dx}=f(\frac{y}{x})$...(*)
- homogeneous: $f(kx,ky)=k^nf(x,y)$
- let $\boxed{u=\frac{y}{x}}$,$\; y(0)=2$
- $y=ux, \; y'=u'x+u\;$ substitue to (*)
- $u'x+u=f(u)$
- $\frac{du}{dx}=\frac{1}{x}(f(u)-u)\;$ [as x≠ 0; [separable equation]
- when $f(u)≠ u$, then $\frac{1}{f(u)-u}du=\frac{1}{x}dx$
- $→\;\boxed{\int\frac{1}{f(u)-u}du=\int\frac{1}{x}dx}$
- ¶1: Solve: $y'=\frac{x-y}{x+y}$
- $\frac{kx-ky}{kx+ky}=\frac{x-y}{x+y}\;→$[homogenous function]
- $\frac{dy}{dx}=\frac{x-y}{x+y}=\frac{1-\frac{y}{x}}{1+\frac{y}{x}}$
- let: $u=\frac{y}{x}\;→y=ux \;→y'=u'x+u$
- $u'x+u=\frac{1-u}{1+u}$
$→\;u'x=\frac{1-2u-u^2}{1+u}$
$→\;\frac{1+u}{1-2u-u^2}du=\frac{1}{x}dx$ [separable equation]
- $\int\frac{1+u}{1-2u-u^2}du=\int\frac{1}{x}dx$
$→\;-\frac{1}{2}\int\frac{-2-2u}{1-2u-u^2}du=\int\frac{1}{x}dx+C$
$→\; \log|1-2u-u^2|+\log(x|^2=C→\;\log|(1-2u-u^2)x^2|=\log e^C$
$→\;|(1-2u-u^2)x^2|=e^C→\;(u^2+2u-1)x^2=±e^C=C$
- when $C=0$ then $u^2+2u-1=0→\;u=-1±\sqrt{2}→\;u'=0$ [SS]
- when $C≠0$ then $(u^2+2u-1)x^2=C→\;(\frac{y^2}{x^2}+2\frac{y}{x}-1)x^2=C$
$→\;y^2+2xy-x^2=C$ [GS]
- ¶2: Solve: $y'=\frac{y^2}{x^2+xy}=\frac{(\frac{y}{x})^2}{1+\frac{y}{x}}$
- let $u=\frac{y}{x}, \; y=ux \;→ y'=u'x+u$
- $u'x+u=\frac{u^2}{1+u}$
- $\frac{du}{dx}=-\frac{u}{1+u}\frac{1}{x}\;$...(**) [separable equation]
- $u=0$ is solution of (**)
- when $u≠ 0$, then $\frac{1+u}{u}du=-\frac{1}{x}dx$
- $\int\frac{1+u}{u}du=-\int\frac{1}{x}dx$
- $\int(1+\frac{1}{u})du=-\int\frac{1}{x}dx$
- $u+\log|u|=-\log|x|+C$
- $\log|ux|=-u+C \;→ |ux|=e^{-u+C}=e^Ce^{-u}$
- $ux=± e^Ce^{-u}=C'e^{-u}\; (C'=± e^C)$
- $\frac{y}x{x}=C'e^{-\frac{y}{x}}$
- $y=C'e^{-\frac{y}{x}}$
- $y=0$ is represented when $C'=0$
- $\therefore \; y=Ce^{-\frac{y}{x}}\;$ [general solution]■
- ¶3: Solve: $y'=\frac{y}{x}+\cos^2\frac{y}{x}, \; y(1)=\frac{\pi}{4}$
- let $u=\frac{y}{x}, \; y=ux$a
- $y'=u'x+u$
- $u'x+u=u+\cos^2u \;→ u'x=\cos^2u$
- $\frac{dy}{dx}=\frac{1}{x}\cos^2u\;$ [separable equation]
- when $\cos u≠0 \;→ \frac{1}{\cos^2 u}du=\frac{1}{x}dx$
- $\int\frac{1}{\cos^2 u}du=\int\frac{1}{x}dx$
- $\tan u=log|x|+C \;→ \tan\frac{y}{x}=log|x|+C$
- $y(1)=\frac{\pi}{4} \;→ \tan\frac{\pi}{4}=\log|1|+C \;→ C=1$
- $\therefore \tan\frac{y}{x}=\log|x|+1$■
2. 同次形:
- homogeneous: 同次形、斉次形
- inhomogeneous: 非同次、非斉次
- separable equation: 変数分離式
- homogeneous=nonzero terms all have the same degree; i.e.,
$ax^2+bxy+cy^2 (abc≠0)$is a homogenous polynomial of degree-2 in two variables.
- $F(kx, ky)=k^nF(x,y)$
- >Top <微分公式>:
- $y=fg\\
\log y=\log(fg)=\log f+\log g\\
\frac{y'}{y}=\frac{f'}{f}
+\frac{g'}{g}\\
y'=f'g+fg'$
- $y=(\frac{f}{g})$
$\log y=\log\frac{f}{g}
=\log f-\log
g\\
\frac{y'}{y}=\frac{f'}{f}
-\frac{g'}{g}\\
y'=\frac{f'}{g}-\frac{fg'}{g^2}
=\frac{f'g-fg'}{g^2}$
- $(e^x)'=e^x$
- $(a^x)'=a^x\log a$
- $y=(x^x)'$
$\log y=x\log x$
$\frac{y'}{y}=\log x+1\\
y'=y(\log x+1)=x^x(\log x+1)$
- $(\log x)'=\frac{1}{x}$
- $(\log y)'=\frac{y'}{y}$
- $(\log_ax)'\\
=(\frac{\log x}{\log a})'\\
=\frac{1}{\log a}(\log x)'\\
=\frac{1}{x\log a}
$
- >Top <積分公式> Integral formula:
- $\int\frac{1}{x}=\log|x|+C$
- $\int \frac{f'}{f}=\log|f|+C$
- $\int a^xdx=\int e^{x\log adx}\\
→\frac{1}{\log a}e^{x\log a}+C\\
=\frac{a^x}{\log a}+C$
- $\int\log xdx\\
=\int x'\log xdx\\
=x\log x-x(\log x)'dx\\
=x\log x-\int dx\\
=x(\log x-1)+C$
>Top 3. First-order linear differential equation (LDE):
-
$\frac{dy}{dx}+p(x)y=q(x)$...(*)
- if $q(x)=0\;$ [homogenous DE; separable DE]
- if $q(x)≠0\;$ [inhomogenous DE]
- solve: $y'+p(x)y=0$...(**) [associated eq]
$dy=-p(x)ydx→\;\frac{1}{y}dy=-p(x)dx\\
→\int \frac{1}{y}=-\int p(x)dx\\
\log|y|=-\int p(x)dx+C →\; y=±e^Ce^{-\int p(x)d}→\; y=Ce^{-\int p(x)dx}$
[GS of (**)]
- (i) [variation of constant, VC]
- assume: $\boxed{y=C(x)e^{-\int p(x)dx}}$ is SS of (*)
substitute: $(C(x)e^{-\int p(x)dx})'+p(x)C(x)e^{-\int p(x)dx}=q(x)$
- $→C'(x)e^{-\int p(x)dx}+C(x)(-p(x)e^{-\int p(x)dx})+p(x)C(x)e^{-\int p(x)dx}=q(x)$
$→C'(x)e^{-\int p(x)dx}=q(x)$
- $\therefore dC(x)=q(x)e^{\int p(x)dx}dx$
- then, $\int dC(x)=\int q(x)e^{\int p(x)dx}dx$
$C(x)=\int q(x)e^{\int p(x)dx}dx+C$
- >Top then subtitute:
$y=e^{-\int p(x)dx}(\int q(x)e^{\int p(x)dx}dx+C)$ [GS of (*)=1LDE]■
- (ii) [integrating factor, IF]
- multiply both sides: $\boxed{e^{\int p(x)dx}}$
then: $y'e^{\int p(x)dx}+yp(x)e^{\int p(x)dx}=q(x)e^{\int p(x)dx}\\
(ye^{\int p(x)dx})'=q(x)e^{\int p(x)dx}\\
ye^{\int p(x)dx}=\int
q(x)e^{\int p(x)dx}dx+C$
$\boxed{\therefore y=e^{-\int p(x)dx}\left(\int q(x)e^{\int p(x)dx}dx+C\right)}$ ■
- ¶1: Solve: $y'-\frac{1}{x}y=0$
- [multiply IF on both sides: $e^{\int p(x)dx}=-\frac{1}{x}$]
- $\frac{1}{x}y'-\frac{1}{x^2}y=0$
- $(\frac{1}{x}y)'=0$
- $\frac{1}{x}y=C \;\therefore y=Cx$■
- ¶2: Solve: $y'+xy=x$
- [multiply: e^{\int xdx}=e^{\frac{x^2}{2}}]
- $e^{\frac{x^2}{2}}y'+xe^{\frac{x^2}{2}}y=xe^{\frac{x^2}{2}}$
- $(e^{\frac{x^2}{2}}y)'=xe^{\frac{x^2}{2}}$
- $\int (e^{\frac{x^2}{2}}y)'dx=\int xe^{\frac{x^2}{2}}dx$
- $e^{\frac{x^2}{2}}y=e^{\frac{x^2}{2}}+C$
- $\therefore y=1+Ce^{-\frac{x^2}{2}}$■
- ¶3: Solve: $y'-xy=2x$
- [multiply: $e^{\int -xdx}=e^{-\frac{1}{2}x^2+C}=Ce^{-\frac{1}{2}x^2}$]
$Cy'e^{-\frac{1}{2}x^2}-Cxye^{-\frac{1}{2}x^2}=C2xe^{-\frac{1}{2}x^2}$
→$(ye^{-\frac{1}{2}x^2})'=2xe^{-\frac{1}{2}x^2}$
→$ye^{-\frac{1}{2}x^2}=\int 2xe^{-\frac{1}{2}x^2}dx$
- when, $x^2=t$, then $2xdx=dt$
$→\int 2xe^{-\frac{1}{2}x^2}dx=\int e^{-\frac{1}{2}t}dt
=-2e^{-\frac{1}{2}t}+C=-2e^{-\frac{1}{2}x^2}+C$
- $ye^{-\frac{1}{2}x^2}=-2e^{-\frac{1}{2}x^2}+C$
$\therefore y=Ce^{\frac{1}{2}x^2}-2$■
- ¶4: $y'+2xy=2x\;$ SS is $y=1$
- $y'+2xy=0 \;→ \frac{1}{y}dy=-2xdx \;→ y=Ce^{-x^2}$
- $\therefore y=Ce^{-x^2}+1$■
- ¶5: Solve: $y'+(\sin x)y=2\sin x$
- [multiply]: $e^{\int\sin xdx}=e^{-\cos x}$]
- $e^{-\cos x}y'+e^{-\cos x}(\sin x)y=2\sin xe^{-\cos x}$
- $(e^{-\cos x}y)'=2\sin xe^{-\cos x}$
- $e^{-\cos x}y=\int 2\sin xe^{-\cos x}=2e^{-\cos x}+C$
- $\therefore y=2+Ce^{\cos x}$■
- ¶6: Solve: $y'+3\frac{\cos x}{\sin x}y=\cos x$
- [multiply both sides: $e^{\int f(x)dx},\; 0<x<\frac{\pi}{2}$]
$\int f(x)dx=\int e^{\frac{\cos x}{\sin x}}=\int e^{\frac{(\sin x)'}{\sin x}}
=e^{e\log\sin x}=\sin^3x$ [IF]
- then: $y'\sin^3 x+3\cos x(\sin^2x)y=\cos x\sin^3x$
$→\;(y\sin^3x)'=(\sin x)'\sin^3x$
$→\;\int (y\sin^3x)'=$\int (\frac{1}{4}\sin^4x)'
$→\;y\sin^3x=\frac{1}{4}\sin^4x+C$
- $\therefore\; y=\frac{1}{4}\sin x+\frac{C}{\sin^3x}$■
- ¶7: Solve: $y'-(2x+1)y=2xe^x$ ...(*)
- first solve: $y'-(2x+1)y=0 \;→ y=Ce^{x^2+x} \; $(C: arbitrary constant)
- here: $y=C(x)e^{x^2+x}
\;→ C'(x)e^{x^2+x}+(2x+1)C(x)e^{x^2+x}-(2x+1)C(x)e^{x^2+x}=2xe^x$
$C'(x)=2xe^{-x^2} \;→ C(x)=-e^{-x^2} \;→ y=-e^x$ [one of special solution]
- $\therefore y=Ce^{x^2+x}-e^x$■
- ¶8: Solve: $y'+\frac{2}{x}y=x$
- [multiply on both sides]: $e^{\int p(x)dx}=e^{\int\frac{2}{x}}dx=e^{\log x^2}=x^2$]
$x^2y'+2xy=x^3 \;→ (x^2y)'=x^3 \;→ x^2y=\frac{x^4}{4}+C$
- $\therefore y=\frac{x^2}{4}+\frac{C}{x^2}$■
3. 一階線形微分方程式:
- variation of constant: 定数変化法
- integrating factor: 積分因子
- associated equation: 同伴方程式
- $y'+Py=Q$
$\frac{d}{dx}X=\widetilde{Q}(x)$
$X=\int\widetilde{Q}dx+C$
[$X$: composite funtion]
- $Ry'+RPy=\frac{d}{dx}Gy=Gy'+G'y$
$G=R, G'=RP \rightarrow R'=RP$
$\frac{dR}{R}=Pdx$
$\int\frac{dR}{R}=\int Pdx$
$\log|R|=\int Pdx+C_1$
$R=Ce^{\int Pdx}\;(C\equiv± e^{C_1})$
- $e^{*}y'+e^{*}Py=e^{*}Q$
$*=\int P(x)dx$
$\frac{d}{dx}(e^{*}y)=e^{*}Q$
$e^{*}y=\int e^{*}Q+C$
$\boxed{y=e^{-*}\left(\int Qe^{*}+C\right)}$
-
$e^{\int P(x)dx}$...[integrating factor]
>Top 4. Jakob Bernoulli DE:
-
$y'+p(x)y=q(x)y^{n} \;(n≠ 0, 1)$ [nonlinear DE]
- when $y^{n}≠ 0$, divide both sides by: $\boxed{y^{n}}$
- $y^{-n}y'+p(x)y^{1-n}=q(x)$
- let $\boxed{u=y^{1-n}}$$\;→ u'=(1-n)y^{-n}y'$
$\frac{1}{1-n}u'+p(x)u=q(x)\;→ u'+(1-n)p(x)u=(1-n)q(x)\;$ [1st LDE]
- ¶1: Solve: $y'+\frac{1}{x}y=x^2y^3$
- multiply $\frac{1}{y^3}$
$\frac{1}{y^3}y'+\frac{1}{x}\frac{1}{y^2}=x^2$
$y^{-3}y'+\frac{1}{x}y^{-2}=x^2$
- multiply $(1-3)=-2$
$-2y^{-3}y'+(-2)y^{-2}\frac{1}{x}=-2x^2$
$(y^{-2})'+(-2)y^{-2}\frac{1}{x}=-2x^2$
- let $u=y^{-2}, \;→u'-\frac{2}{x}u=-2x^2$ [1st LDE]
- formula: $y'+p(x)y=q(x) \;→y=e^{-\int p(x)dx}(\int q(x)e^{\int p(x)dx}dx+C)$
- here: $p(x)=-\frac{2}{x}, \;q(x)=-2x^2$
$e^{-\int p(x)dx}=e^{-\int -\frac{2}{x}dx}=e^{2\log|x|}=e^{\log x^2}=x^2$
$e^{\int p(x)dx}=e^{\int -\frac{2}{x}dx}=e^{-2\log|x|}=e^{\log x^{-2}}=x^{-2}$
- $u=x^2(\int -2x^2・x^{-2}dx+C)=x^2(\int -2dx+C)=x^2(-2x+C)=-2x^3+Cx^2$
- $u=y^{-2} \;→y^{-2}=-2x^3+Cx^2$:
$-2x^3y^2+Cx^2y^2=1$
- ¶2: Solve: $y'+y=e^xy^2$...(*)
- $y=0$ is solution of (*)
- when $y≠ 0$, divide both side by $y^2$
$y^{-2}y'+y^{-1}=e^x$
- let $u=y^{-1} \;→ u'=-y^{-2}y'$
- $u'-u=-e^x\;$ [linear DE] ...(**)
- solve $u'-u=0 \;→ u=Ce^x$
- here, substitute $C \;→ C(x)$ to (**)
$C'(x)e^x+C(x)e^x-C(x)e^x=-e^x \;→ C'(x)=-1\;→ C(x)=-x\;$ [special s.]
- then, $u=-xe^x$ is a SS of (*)
- $\therefore u=Ce^x-xe^x=e^x(C-x)$
- $y=\frac{1}{e^x(C-x)} →$ solution of $y=0$ can be when $C=\infty$ [GS]■
- ¶3: Solve: $y'+\frac{2}{x}y=x^2\sin x・y^2$
- let: $z=y^{1-2}=y^{-1}\;→ z'=-y^{-2}y'$
- multiply: $-y^{-2}y'+\frac{2}{x}(-y^{-2})y=x^2\sin x(-y^{-2})y^2$
- $z'-\frac{2}{x}z=-x^2\sin x$ [LDE]
- multiply: $e^{\int -\frac{2}{x}}=e^{-2\log|x|}=\frac{1}{x^2}$
- $\frac{1}{x^2}z'-\frac{2}{x^3}z=-\sin x$
$\frac{d}{dx}(\frac{z}{x^2})=-\sin x$
$\frac{z}{x^2}=\int -\sin xdx=\cos x+C$
$z=x^2(\cos x+C)$
- return: $y=z^{-1}=\frac{1}{x^2(\cos x+C)}$:■
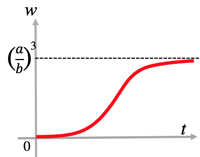
- ¶ 4: Solve: [Ludwig von Bertalanffy model: growth curve]
- $w'=aw^{\frac{2}{3}}-bw, \; w(0)=0$...(*)
- $w'+bw=aw^{\frac{2}{3}}$ [Bernoulli DE]
- when $w≠0$ divie both sides by $w^{\frac{2}{3}}$
- $w^{-\frac{2}{3}}w'+bw^{\frac{1}{3}}=a$
- let $u=w^{\frac{1}{3}}\;→ u'=\frac{1}{3}w^{-\frac{2}{3}}w'$
- $u'+\frac{b}{3}u=\frac{a}{3}$ [linear DE]...(**)
- first solve $u'+\frac{b}{3}u=0 \;→ u=Ce^{-\frac{b}{3}t}$
- and (**) has SS of $u=\frac{a}{b}$
- then $u=Ce^{-\frac{b}{3}t}+\frac{a}{b}$
- $\therefore w=(Ce^{-\frac{b}{3}t}+\frac{a}{b})^3$
- here $w(0)=0 \;→ C=-\frac{a}{b}$
- the solution of (*) is $w=(\frac{a}{b})^3(1-e^{-\frac{b}{3}t})^3$ (>Fig.)■
4. ベルヌーイ微分方程式:
<Point>:
- $y'+P(x)y=Q(x)y^n$
- n=0: 1LDE
- n=1: separable
- let: $z=y^{1-n}$
- multply: $z'=(1-n)y^{-n}y'$
- solve: LDE of $z$
- replace: $y=z^{\frac{1}{1-n}}$
- Growth curve:
- Re:
- $\log_aa^p=p$
- $a^{\log_aM}=M$
>Top 5. Yacopo Riccati DE:
-
$y'+r(x)y^2+p(x)y=q(x)$...(*) [nonlinear DE]
- this is only solvable when SS is known; SS of above (*) is $y_1$:
- let: $\boxed{y=y_1+u}$ to (*):
$y_1'+u'+r(x)(y_1+u)^2+p(x)(y_1+u)=q(x)$
$→y_1'+u'+r(x)(y_1^2+2y_1u+u^2)+p(x)(y_1+u)=q(x)$
$(y_1'+r(x)y_1^2+p(x)y_1-q(x))+u'+2r(x)y_1u+r(x)u^2+p(x)u=0$
- here: $y_1$ is SS of (*)
$→ u'+2r(x)y_1u+r(x)u^2+p(x)u=0$
$→ u'+(2r(x)y_1+p(x))u=-r(x)u^2$
- let: $s(x)=2r(x)y_1+p(x)$
$\boxed{u'+s(x)u=-r(x)u^2}$ [Bernoulli DE]
- multiply $u^{-2}$
$u^{-2}u'+s(x)u^{-1}=-r(x)$
- multiply (1-2)=-1:
$-u^{-2}u'-s(x)u^{-1}=r(x)$
$→(u^{-1})'-s(x)u^{-1}=r(x)$
- let $u^{-1}=t$
$t'-s(x)t=r(x) \;→t'+T(x)t=r(x)$ [1st LDE]
- ¶1: Solve: $y'+xy^2-(2x^2+1)y=-x^3-x+1$; here SS is $y_1=x$..(*)
- let: $y=x+u$...(**)
$1+u'+x(x+u)2-(2x^2+1)(x+u)=-x^3-x+1$
$\;→u'+x^3+2x^2u+xu^2-2x^3-2x^2u-x-u=x^3-x$
$u'+xu^2-u=0\;→u'-u=-xu^2$ [Bernoulli's DE, n=2]
- multiply $u^{-2}$
$u^{-2}u'-u^{-1}=-x$
- multiply $1-2=-1$
$-u^{-2}u'+u^{-1}=x$
$(u^{-1})'+u^{-1}=x$
- here $u^{-1}=t$
$t'+t=x$ [1st LDE]
- formula: $y=e^{-\int p(x)dx}(\int q(x)e^{\int p(x)dx}dx+C)$
here: $p(x)=1, q(x)=x$
$e^{-\int p(x)dx}=e^{-int dx}=e^{-x}$
$e^{\int p(x)dx}=e^{int dx}=e^x$
$→ t=e^{-x}(\int xe^xdx+C)=e^{-1}(xe^x-e^x+C)=x-1+Ce^{-1}$
- here: u=y-x [from (**)]
$
t=u^{-1}=\frac{1}{y-x}$
$\frac{1}{y-x}=Ce^{-1}+x-1$
$\therefore y=\frac{1}{Ce^{-1}+x-1}+x$ [GS of (*)]
5. リッカチ微分方程式:
- 部分積分法:
- $\int fg'=fg-\int f'g$
- $\int xe^xdx=xe^x-e^x$
>Top 6. Exact DE:
-
$M(x,y)dx+N(x,y)dy=0$...(*) [Exact DE]
- [Point]
- if a differentiable function $M(x,y), N(x,y)$ on a simply connected area $(x-y)$
plane satisfies:
$\frac{\partial}{\partial y}M(x,y)=\frac{\partial}{\partial x}N(x,y)$...(*)
- $M(x,y)dx+N(x,y)dy=0$...(**) [exact DE]
- $\mathrm{rot} \pmatrix{M\\N\\L}=\textbf{0}$...(*3)
- $\pmatrix{\frac{\partial}{\partial x}\\\frac{\partial}{\partial y}\\
\frac{\partial}{\partial z} }\times \pmatrix{M\\N\\L}
=\pmatrix{\frac{\partial}{\partial y}L-\frac{\partial}{\partial z}N\\
\frac{\partial}{\partial z}M-\frac{\partial}{\partial x}L\\
\frac{\partial}{\partial x}N-\frac{\partial}{\partial y}M}$
- when (*3) is satisfied: $Mdx+Ndy+Ldx=0$
- Solution of $Mdx+Ndy=0$:
- step1: confirm $\frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}$
- step2: pursue scalar potential $\varphi$ of vector $\pmatrix{M\\N\\O}$
- step3: the solution is $\varphi=C$; to pursue $\varphi$:
$\pmatrix{M\\N\\O}=\pmatrix{\frac{\partial\varphi}{\partial x}\\
\frac{\partial\varphi}{\partial y}\\\frac{\partial\phi}{\partial z}}\;→\frac{\partial\varphi}{\partial x}=M, \; \frac{\partial\varphi}{\partial y}=N$
- [Total differentiation & Exact DE]
- differential form: $p(x,y)dx+q(x,y)dy=0$
$df(x,y)=\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy
=p(x,y)dx+q(x,y)dy=0$
- $p(x,y)dx+q(x,y)dy=0\;$ [GS]
- when $p(x,y)dx+q(x,y)dy=0$ is exact DE
$\Leftrightarrow \frac{\partial p(x,y)}{\partial y}=\frac{\partial q(x,y)}{\partial x}\;$
[necessary & sufficient condition]
- $\boxed{df(x,y)=\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy
=p(x,y)dx+q(x,y)dy=0}$
from $\boxed{df(x,y)=0→ f(x,y)=C}$
- from, $\frac{\partial f(x,y)}{\partial x}=p(x,y),\; \frac{\partial f(x,y)}{\partial y}=q(x,y)$
then, $\frac{\partial^2f(x,y)}{\partial x\partial y}=\frac{\partial p(x,y)}{\partial y},\;
\frac{\partial^2f(x,y)}{\partial y\partial x}=\frac{\partial q(x,y)}{\partial x}$
- from Schwarz condition: $\frac{\partial^2f(x,y)}{\partial x\partial y}
=\frac{\partial^2f(x,y)}{\partial y\partial x}
→ \frac{\partial p(x,y)}{\partial y}=\frac{\partial q(x,y)}{\partial x}$ [necessary condition]
- let $f(x,y)=\int p(x,y)dx+C(y),\; p(x,y)=\frac{\partial f(x,y)}{\partial x}$
- integrate both sides: $f(x,y)=\int p(x,y)dx+C(y)$
- partial integrate both sides by $y:\;\frac{\partial f(x,y)}{\partial y}
=\frac{\partial}{\partial y}\int p(x,y)dx+\frac{\partial C(y)}{\partial y}$
- if $\frac{\partial f(x,y)}{\partial y}=q(x,y)$ is true, then:
$q(x,y)=\frac{\partial}{\partial y}\int p(x,y)dx+\frac{\partial C(y)}{\partial y}$
$\therefore \frac{\partial C(y)}{\partial y}=q(x,y)-\frac{\partial}{\partial y}\int p(x,y)dx$
- partial integrate both sides by $x$:
$\frac{\partial}{\partial x}\left(q(x,y)-\frac{\partial}{\partial y}\int p(x,y)dx\right)
=\frac{\partial q(x,y)}{\partial x}-\frac{\partial^2}{\partial x\partial y}\int p(x,y)dx
=\frac{\partial q(x,y)}{\partial x}-\frac{\partial}{\partial y}
\left(\frac{\partial}{\partial x}\int p(x,y)dx\right)$
$=\frac{\partial q(x,y)}{\partial x}-\frac{\partial p(x,y)}{\partial y}=0$
$\therefore q(x,y)-\frac{\partial}{\partial y}\int p(x,y)dx$ can be $f(x)$
then $^\exists C(y)$ such that $\frac{\partial C(y)}{\partial y}
=q(x,y)-\frac{\partial}{\partial y}\int p(x,y)dx$
- from: $\frac{\partial f(x,y)}{\partial y}=q(x,y)$...(*) then,
$\frac{\partial f(x,y)}{\partial y}=\frac{\partial}{\partial y}\int p(x,y)dx
+\frac{\partial C(y)}{\partial y}$...(**)
- integrate both sides of (**) by $y$:
$f(x,y)=\int p(x,y)dx+C(y)$
- from integrate (*): $C(y)=\int \left(q(x,y)-\frac{\partial}{\partial y}\int p(x,y)dx\right)dy$
$\therefore \boxed{f(x,y)=\int p(x,y)dx+\int\left(q(x,y)
-\frac{\partial}{\partial y}\int p(x,y)dx\right)dy,\;
f(x,y)=C}$
- ¶1: $2x\log y+\frac{x^2}{y}\frac{dy}{dx}=0$
- $2x\log ydx+\frac{x^2}{y}dy=0\;$ [exact DE: $Mdx+Ndy=0$]
- $\frac{\partial}{\partial y}(2x\log y)=\frac{2x}{y},\;
\frac{\partial}{\partial x}(\frac{x^2}{y})=\frac{2x}{y}$ [exact DE]
then, $\frac{\partial\phi}{\partial x}=2xlogy$...(1)
$\frac{\partial\varphi}{\partial y}=
\frac{x^2}{y}$...(2)
- from (1): $\varphi=x^2\log y+g(y)$...(3)
- substitute (3) for (2): $\frac{x^2}{y}+g'(y)=\frac{x^2}{y}$
$g'(y)=0 \;→ g(y)=C$
- return to (3): $x^2\log y+C=0$
- Eg.: $M(x,y)dx+N(x,y)dy=0$
- multiply: $u(x,y)$
$u(x,y)M(x,y)dx+u(x,y)N(x,y)dy=0$
$\frac{\partial}{\partial y}(u(x,y)M(x,y))=\frac{\partial}{\partial x}(u(x,y)N(x,y))$
- $u(x)\frac{\partial M}{\partial y}=\frac{du(x)}{dx}N+u(x)\frac{\partial N}{\partial x}$
$\frac{du(x)}{dx}=\frac{1}{N}(\frac{\partial M}{\partial y}
-\frac{\partial N}{\partial x})u(x)\;$ if this will be $f(x)g(u)\;$[separable equation]
- similarly: $\frac{du(y)}{dy}=\frac{1}{M}(\frac{\partial M}{\partial y}
-\frac{\partial N}{\partial x})u(y)\; →f(y)g(u)$ [separable equation]
- ¶2: $(2xy^2+1)dx+x^2ydy=0$...(*)
- $u(x,y)(wxy^2+1)dx+u(x,y)x^2ydy=0$
$\frac{\partial}{\partial y}(u(x,y)(swy^2+1))=
\frac{\partial}{\partial x}(u(xy)x^2y)$
- if, u(x,y)→u(x), then $u(x)4xy=\frac{du}{dx}x^2y+u(x)・2xy$
$2xyu(x)=\frac{du}{dx}x^2y$
$\frac{2}{x}dx=\frac{1}{u}du$[from (*): $x,y≠0$]
$\int\frac{2}{x}dx=\int\frac{1}{u}du$
$\log x^2=\log u\;→u=x^2$ [no need of C]
- then, $\frac{\partial\varphi }{\partial x}=x^2(2xy^2+1)$...(1)
$\frac{\partial\varphi}{\partial y}=x^2・x^2y$...(2)
- from (2): $\varphi=\frac{1}{2}x^4y^2+g(x)$...(3)
substitie (3) for (1):
$2x^3y^2+g'(x)=2x^3y^2+x^2$
→ $g(x)=x^2 \;→g(x)=\frac{1}{3}x^3+C$
$\therefore \varphi=\frac{1}{2}x^4y^2+\frac{1}{3}x^3+C=0$
- ¶3. $(4xy+y^3)dx+(2x^2+3y^2x)dy=0$...(*)
- consider: $p(x,y)dx+q(x,y)dy=0$
$→\frac{\partial p(x,y)}{\partial y}=\frac{\partial}{\partial y}(4xy+y^3)=4x+3y^2$
$\frac{\partial q(x,y)}{\partial x}=\frac{\partial}{\partial x}(2x^2+3y^2x)=4x+3y^2$
$\therefore (*)$ is exact DE.$\; [\frac{\partial p(x,y)}{\partial y}
=\frac{\partial q(x,y)}{\partial x}]$
- formula: $\int p(x,y)dx+\int \left(q(x,y)-\frac{\partial}{\partial y}\int p(x,y)dx\right)dy=C$
- $\int p(x,y)dx=\int (4xy+y^3)dx=2x^2y+y^3\;→\frac{\partial}{\partial y}\int p(x,y)dx
=2x^2
+3y^2x$
$q(x,y)-\frac{\partial}{\partial y}p(x,y)dx=2x^2+3y^2x-(2x^2+3y^2)=0$
$2x^2+y^3x=C$
- ¶3': [another solution] $(4xy+y^3)dx+(2x^2+3y^2x)dy=0$...(*) [exact DE]
- $f(x,y)=\int p(x,y)dx+C(y)=\int (4xy+y^3)dx+C(x)=2x^2y+y^3x+C(y)$
$f(x,y)=\int q(x,y)dy+D(x)=\int (2x^2+3y^2x)dy D(y)=2x^2y+y^3x+D(x)$
- [making for missing terms]: $f(x,y)=2x^2y+y^3x=C$
6. 完全微分方程式:
- exact (total) differential: 完全微分
- differential form: 微分形式
- conservative vector field: 保存ベクトル場
- simply connected area: 単連結領域
- Schwarz integrability condition: $f_ij=f_ji$
- if and only if=iff: 必要十分条件
- >Top Simply connected area (left):
any roop enclosing one or more of the holes cannot be contracted to a point (right).
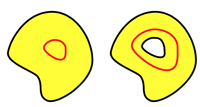
- Necessary & sufficient condition of exact DE of the following:
- $p(x,)dx+q(x,y)dy=0$
$\Leftrightarrow
\frac{\partial p(x,y)}{\partial dy}
=\frac{\partial q(x,y)}{\partial x}
$
- Level of Continuity:
- Continuous: eg: 整数部分
- Differentialble: eg: |x|
- C1 level: continuously differentialble
- C∞ level: eg: $\sin x, \cos x$
>Top 7. Exact DE (II) Integrating factor):
-
$u(x,y)p(xy)dx+u(x,y)q(x,y)dy=0$...(*)
- $df(x,y)=\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy
=p(x,y)dx+q(x,y)dy=0
\;$ [total differentiation; exact DE]
- when $\frac{\partial p(x,y)}{\partial x}≠\frac{\partial q(x,y)}{\partial y}\;$ [not exact DE]
- multipy both sides $u(x,y)$, then (*) can be exact DE.
i.e.: $\frac{\partial}{\partial y}(u(x,y)p(x,y))
=\frac{\partial}{\partial x}(u(x,y)q(x,y))$ , then (*) is exact DE.
- $\frac{\partial u(x,y)}{\partial y}p(x,y)+u(x,y)\frac{\partial p(x,y)}{\partial y}
=\frac{\partial u(x,y)}{\partial x}q(x,y)+u(x,y)\frac{\partial q(x,y)}{\partial x}
$...(**)
[difficult to find integrating factor $u(x,y)$, but can find it if it is either $u(x)$ or $u(y)$]
- in case of $u(x)$ above (**) is
$u(x)\left(\frac{\partial p(x,y)}{\partial y}-\frac{\partial q(x,y)}{\partial x}\right)
=\frac{\partial u(x)}{\partial x}q(x,y)$
$→ \frac{1}{u(x)}\frac{\partial u(x)}{\partial x}
=\frac{1}{q(x,y)}\left(\frac{\partial p(x,y)}{\partial y}-\frac{\partial q(x,y)}{\partial x}\right)$...(*3)
- if (*3) can be $g(x)$, then: $\frac{1}{u(x)}\frac{\partial u(x)}{\partial x}
\frac{1}{q(x,y)}\left(\frac{\partial p(x,)}{\partial y}-\frac{\partial q(x,y)}{\partial x}\right)
=g(x)$ [separable DE]
$→ \int\frac{1}{u(x)}=\int g(x)dx+C\;→\log|u(x)|=\int g(x)+C$
$\therefore u(x)=±e^{\int g(x)dx+C}=±e^C・e^{\int g(x)dx}=Ce^{\int g(x)dx}$
integrating factor is $u(x)=e^{\int g(x)dx}$$=e^{\int \frac{1}{q}(p_y-q_x)dx}$
here:$ [u=u(x,y); \frac{\partial p(x,y)}{\partial y}=p_y ...]
$
- in case of $u(y)$ above $\frac{\partial u(x,y)}{\partial y}p(x,y)+u(x,y)\frac{\partial P(x,y)}{\partial y}
=\frac{\partial u(x,y)}{\partial x}q(x,y)+u(x,y)\frac{\partial q(x,y)}{\partial x}$
$→\frac{\partial u(y)}{\partial y}p(x,y)+u(y)\frac{\partial p(x,y)}{\partial y}
=u(y)\frac{\partial q(x,y)}{\partial x}\;
→-u(y)(\frac{\partial p(x,y)}{\partial y}-\frac{\partial q(x,y)}{\partial x})
=\frac{\partial u(y)}{\partial y}p(x,y)$
$\therefore \frac{1}{u(y)}\frac{\partial u(y)}{\partial y}
=-\frac{1}{p(x,y)}(\frac{\partial p(x,y)}{\partial y}-\frac{\partial q(x,y)}{\partial x})$
let: $\frac{1}{p(x,y)}(\frac{\partial p(x,y)}{\partial y}-\frac{\partial q(x,y)}{\partial x})=h(y)\;→\frac{1}{u(y)}\frac{\partial u(y)}{\partial y}=-h(y)\;$ [separable DE]
then $\int\frac{1}{u(y)}dx=-\int h(y)dy+C\;→\log|u(y)|=-\int h(y)dy+C$
$\therefore u(y)=Ce^{-\int h(y)dy}$
then integarating factor is $u(y)=e^{-\int h(y)dy}$$=e^{-\int \frac{1}{p}(p_y-q_x)dy}$
- ¶1: Solve GS of $(x-\frac{y}{x})dx+(\frac{e^y}{x}-1)dy=0$
- consider as: $p(x,y)dx+q(x,y)dy=0$...(*)
$\frac{\partial p(x,)}{\partial y}-\frac{\partial q(x,y)}{\partial x}=-\frac{1}{x}-(-\frac{e^y}{x^2}≠0$ [non exact DE]
- then $\frac{1}{q(x,y)}(\frac{\partial p(x,y)}{\partial y}-\frac{\partial q(x,y)}{\partial x})
=\frac{-\frac{1}{x}+\frac{e^y}{x^2}}{\frac{e^y}{x}-1}=\frac{e^y-x}{xe^y-x^2}
=\frac{1}{x}
$
- multiply integrating factors: $u(x)=e^{\int \frac{1}{q}(p_y-q_x)dx}=e^{\int \frac{1}{x}}
=
e^{\log x}=x$
- (*) will be: $(x^2-y)dx+(e^y-x)dy=0$ [consider as $r(x,y)dx+s(x,y)dy=0$]
- $\frac{\partial r(x,y)}{\partial y}-\frac{\partial s(x,y)}{\partial x}=-1-(-1)=0$ [exact DE]
- formula GS: $\boxed{\int r(x,y)dx+\int\left(s(x,y)
-\frac{\partial}{\partial y}\int r(x,y)dx\right)dy=C}$
- $→ \frac{1}{3}x^3-xy+\int\left((e^y-x)-\frac{\partial}{\partial y}(\frac{1}{3}x^3-xy\right)dy=C$
- $→ \frac{1}{3}x^3-xy+\int( e^x-x+x)dy=C$
- $\therefore \frac{1}{3}x^3-xy+e^y=C\;→x^3-3xy+3e^y=C$ [GS]■
- ¶1' (another solution):
- $\boxed{f(x,y)=\int r(x,y)dx+C(y)...(1)\\f(x,y)=\int s(x,y)dy+D(x)...(2)}$
- $(1)→=\frac{1}{3}x^3-xy+C(y)$
$(2)→e^y-xy+D(x)$
- supply mutual deviciency: $C(y)=e^y, D(x)=\frac{1}{3}x^3$
$→ f(x,y)=\frac{1}{3}x^3-xy+e^y=C$
$\therefore x^3-3xy+3e^y=C$ [GS]■
7. 完全微分方程式 (II):
>Top 8. Alexis Clairaut DE:
-
$y=xy'+f(y')=0$...(*)
[one of Nonlinear DE]
- differentiate both sides: $y'=y'+xy''+f'(y')y''\;→y''(x+f'(y'))=0$
- 1) when: $y''=0\;→y'=C$
- substitute (*): $\boxed{y=Cx+f(C)=0}\;$ [GS]
$y=y'+x$
- 2) when: $(x+f'(y'))=0\;→\boxed{x=-f'(y')}$...(a)
- substiture (*): $\boxed{y=-f'(y')y'+f(y')=0}$...(b)
- eliminate or parameterise $y'$ by (a)(b): [Singular Solution in cases]:
- ¶1.: $y=xy'-(y')^2$
- diffrentiate both sides: $y'=y'+xy''-2(y')y''\;→y''(x-2y')=0$
- 1) when: $y''=0\;→y'=C$
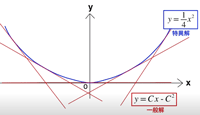
- substitute (*): $y=Cx-C^2\;$ [GS]
- 2) $x-2y'=0\;→y'=\frac{1}{2}x$
- substitute (*): $y=\frac{1}{2}x^2-\frac{1}{4}x^2=\frac{1}{4}x^2\;$: [Singular S]
8. クレロー微分方程式:
- singular solution: 特異解
- envelope: 包絡線
- ¶1: Clauaut curve:
>Top 9. d'Alembert's (Lagrange's) DE:
-
$y=xf(y')+g(y')=0$...(*)
- when $f(y')=y' \;→$ Clairaut's DE; here consider: $f(y')≠y'$
- differentiate both sides: $y'=f(y')+xf'(y')y''+g'(y')y''\;→y''(xf'(y')+g'(y'))=y'-f(y')$
- let $y'=p:\; p'(xf(p)+g'(p))=p-f(p)$...(*)
- from $f(y')≠y',\; y'=p\;→p-f(p)≠0$
- divide by: $p-f(p)\;→\frac{xf(p)+g'(p))}{p-f(p)}=\frac{1}{p'}$
$\;→\frac{1}{p'}-\frac{f'(p)}{p-f(p)}x=\frac{g'(p)}{p-f(p)}$
- as: $\frac{1}{p'}=\frac{1}{\frac{dp}{dx}}=\frac{dx}{dp}$
$\;→\frac{dx}{dp}-\frac{f'(p)}{p-f(p)}x=\frac{g'(p)}{p-f(p)}$
- let: $P_0(p)=-\frac{f'(p)}{p-f(p)}; Q_0(p)=\frac{g'(p)}{p-f(p)}$
then: $\frac{dx}{dp}+P_0(p)x=Q_0(p)\; $ [1st LDE of function $p$]
- thus:
$\boxed{1) y=xf(p)+g(p)\\
2) x=e-{\int P_0(p)dp}\left(\int Q_0(p)e^{\int P_0(p)dp}dp+C\right)}$
eliminate or parameterize $p$ from 1) and b).
- ¶1: $y=x(y'+1)+(y')^2$
- differentiate both sides: $y'=(y'+1)+xy''+2y'y''$
- let: $y'=p\;→p=(p+1)+xp'+2pp'\;→-(xp'+2pp')=1\;→-(x+2p)p'=1$
- divide by $p'\;→-(x+2p)=\frac{1}{p'}\;→\frac{1}{p'}+x=-2p$:
- then: $\frac{1}{p'}=\frac{dx}{dp}\;→\frac{dx}{dp}+x=-2p\;$ [1st LDE]
- from the formula: $P_0(p)=1; Q_0(p)=-2$
- thus: $x=e^{-\int dp}(\int -2pe^{\int dp}dp+C)=e^{-p}(\int -2pe^pdp+C)$
- $=e^{-p}(-2pe^p+2e^p+C)\; ←[\int fg'=fg-\int f'g]$
$→x=Ce^{-p}-2p+2$; y=x(p+1)+p^2\;$ [parameterized solution]
9. ダランベール(ラグランジェ)微分方程式:
>Top 10. Second-order linear differential equation & Wronskian:
-
$\frac{d^2y}{dx^2}+p(x)\frac{dy}{dx}+q(x)y=r(x)$
- $y''+p(x)y'+q(x)y=r(x)\;$...(1) where, GS of (1) is $y$ and SS of (1) is $y_0$
- $y''+p(x)y'+q(x)y=0$...(2) GS of (2) is $Y$ [associated eq=homogenous DE]
- then: $\boxed{y=y_0+Y}$
- $\because y_0''+p(x)y_o'+q(x)y_0=r(x)$...(3)
- (1)-(3): $(y-y_0)''+p(x)(y-y_0)'+q(x)(y-y_0)=0\;→y-y_0=Y$ is GS of (3)
$\therefore y=y_0+Y$
- GS of (2) is Y; let $y_1, y_2$ are solutions of (2), then $Y=C_1y_1+C_2y_2$
- $\because (C_1y_1+C_2y_2)''+p(x)(C_1y_1+C_2y_2)'+q(x)(C_1y_1+C_2y_2)$
$=C_1(y_1''+p(x)y_1'+q(x)y_1)+C_2(y_1''+p(x)y_1'+q(x)y_1)
=0$
$\;→ Y=C_1y_1+C_2y_2\; [y_1, y_2\;$ linear independent, and are FS]
- Wronskian:
- when: $y_1, y_2$ are solutions of (2) [discriminant of linear dependence]
- Wronskian: $W(y_1, y_2)=\pmatrix{y_1&y_2\\y_1'&y_2'}$
- differentiate both sides: $C_1y_1+C_2y_2=0\;→C_1y_1'+C_2y_2'=0$
$\pmatrix{C_1y_1+C_2y_2\\C_1y'+C_2y_2'}=\pmatrix{0\\0}
\;\therefore \pmatrix{y_1&y_2\\y_1'&y_2'}\pmatrix{C_1\\C_2}=
\pmatrix{0\\0}$
- when, $W(y_1,y_2)≠0, \;^\exists\pmatrix{y_1&y_2\\y_1'&y_2'}^{-1}$
then, $\pmatrix{C_1\\C_2}=\pmatrix{0\\0}$
$\therefore, W(y_1, y_2)≠0 \;→y_1, y_2$ are linear independent.
- Re: [nth LDE has n-number of independent solutions.]
- when, $y''+p(x)y'+q(x)y=0$ has 3 solutions $y_1, y_2, y_3$ which are not necessarily linear independent.
$\because, y_1''+p(x)y_1'+q(x)y_1=0, y_2''+p(x)y_2'+q(x)y_2=0, y_3''+p(x)y_3'+q(x)y_3=0$
then, $W(y_1,y_2,y_3)=\pmatrix{y_1&y_2&y_3\\y_1'&y_2'&y_3'\\y_1''&y_2''&y_3''}
=\pmatrix{y_1&y_2&y_3\\y_1'&y_2'&y_3'\\0&0&0}=\mathbb{0}$
- ¶1: FS of $y''-3y'+2y=0$ is $y_1=e^x, y_2=e^{2x}$,
and SS of $y''-3y'+2y=e^{3x}$...(*) is $y_0=\frac{1}{2}e^{3x}$,
then pursue GS of (*):
- Wronskian of FS: $\;W(y_1,y_2)=\pmatrix{y_1&y_2\\y_1'&y_2'}
=\pmatrix{e^x&e^{2x}\\e^x&2e^{2x}}=2e^{3x}-e^{3x}=e^{3x}≠0$
$\;→y_1, y_2$ are linear independent.
- input $y_0=\frac{1}{2}e^{3x}$ to (*)$\;→\frac{9}{2}e^{3x}-\frac{9}{2}e^{3x}+e^{3x}=e^{3x}$ [SS]
- then, $Y=C_1e^x+C_2e^{2x}$
- $y=y_0+Y=\frac{1}{2}e^{3x}+C_1e^x+C_2e^{2x}$
10. 二階線形微分方程式とロンスキアン:
- fundamental solution (FS): 基本解
- Wronski determinant (Wronskian): ロンスキー行列式
- discriminant: 判別式
>Top 11. Constant coefficient secont-order homogeneous DE (I):
-
$\frac{d^2y}{dx^2}+a\frac{dy}{dx}+by=o$...(*)
- Assume: either FS ($y_1, y_2$) of (*) as $\boxed{y=e^{\lambda}}$
- Consider GS of (*) is $y=C_1y_1+C_2y_2\;→y'=\lambda e^{\lambda x},\;
y''=\lambda^2 e^{\lambda x}$
- $\lambda^2 e^{\lambda x}+a\lambda e^{\lambda x}+be^{\lambda x}=0\;→(\lambda^2+a\lambda+b)e^{\lambda x}=0$
- as $e^{\lambda x}>0\;→ (\lambda^2+a\lambda+b)=0\;$...(**)
- 1) $D=a^2-4b>0$ :(*) has two different real solutions of (**):\;
$e^{\lambda_1x}, e^{\lambda_2x}$
Wronskian: $W(y_1,y_2)=\pmatrix{y_1&y_2\\y_1'&y_2'}
=\pmatrix{e^{\lambda_1x}&e^{\lambda_2x}\\
\lambda_1e^{\lambda_1x}&\lambda_2e^{\lambda_2x}}
=e^{\lambda_1+\lambda_2)x(\lambda_1-\lambda_2)}≠0\;$
[linear dependent; and are FS of (**)]
$\therefore\; y=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}$ are GS of (*)
- 2) $D=a^2-4b=0\;→y_1=e^{\lambda_1x}$ is one of FS of (*)
let another linear dependent solution $y_2=xe^{\lambda_1x}$
$\;→y_2'=e^{\lambda_1x}+\lambda_1xe^{\lambda_1x}=e^{\lambda_1x}(1+\lambda_1x)$
$\;→y_2''=\lambda_1e^{\lambda_1x}+\lambda_1e^{\lambda_1x}
+\lambda_1^2xe^{\lambda_1x}=(2\lambda_1+x\lambda_1^2)e^{\lambda_1x}$
substitute to (*):
$(2\lambda_1+x\lambda_1^2)e^{\lambda_1x}
+a(1+\lambda_1x)e^{\lambda_1x}+bxe^{\lambda_1x}
=(\lambda_1^2+a\lambda_1+b)xe^{\lambda_1x}+(2\lambda_1+a)e^{\lambda_1x}=0$
as double root of (*):$\;-\frac{a}{2}=\lambda_1\;→2\lambda_1+a=0$
thus: \; $y_2=xe^{\lambda_1x}$ is a solution of (**)
- $W(y_1,y_2)=\pmatrix{y_1&y_2\\y_1'&y_2'}=\pmatrix{e^{\lambda_1x}&xe^{\lambda_1x}
\\\lambda_1e^{\lambda_1x}&(\lambda_1x+1)e^{\lambda_1x}}$
$=(\lambda_1x+1)e^{2\lambda_1x}-\lambda_1xe^{2\lambda_1x}=e^{2\lambda_1x}≠0$
thus: $y_1=e^{\lambda_1x}, y_2=xe^{\lambda_1x}$ are linear independent solution [BS]
then: $y=(C_1+C_2x)e^{\lambda_1x}$ is GS of (*)
- 3) $D=a^2-4b<0\;$→(*) has two different imaginary root $y_1=e^{\lambda_1x}, y_2=e^{\lambda_2x}\;$ [FS]
here: $\lambda_1=\alpha+i\beta, \;\lambda_2=\alpha-i\beta$
where $\alpha=-\frac{a}{2},\; \beta=\frac{\sqrt{4b-a^2}}{2}$,
then: $y_1=e^{(\alpha+i\beta)x},\; y_2=e^{(\alpha-i\beta)x}$
- $W(y_1,y_2)=\pmatrix{y_1&y_2\\y_1'&y_2'}=\pmatrix{e^{\lambda_1x}&e^{\lambda_2x}
\\\lambda_1e^{\lambda_1x}&\lambda_2e^{\lambda_2x}}$
$=\lambda_2e^{(\lambda_1+\lambda_2)x}-\lambda_1e^{(\lambda_1+\lambda_2)x}
=(\lambda_2-\lambda_1)e^{(\lambda_1+\lambda_2)x}=-2i\beta e^{2\alpha x}≠0\;$
[linear dependent FS]
- $\therefore\; y=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}
=C_1e^{\alpha+i\beta}+C_2e^{\alpha-i\beta}=
C_1e^{\alpha x}e^{i\beta x}+C_2e^{\alpha x}e^{-i\beta x}$
$=C_1e^{\alpha x}(\cos\beta x+i\sin\beta x)+C_2e^{\alpha x}((\cos(-\beta x)+i\sin (-\beta x))$
$=C_1e^{\alpha x}(\cos\beta x+i\sin\beta x)+C_2e^{\alpha x}(\cos\beta x-i\sin\beta x)$
$=e^{\alpha x}((C_1+C_2)\cos\beta x+i(C_1-C_2)\sin\beta x)$
here: →$C_1+C_2=C_3,\;i(C_1-C_2)=C_4$
$\therefore \;y=e^{\alpha x}(C_3\cos\beta x+C_4\sin\beta x)\;→$ [GS of (*)]
- to confirm: $y_1=e^{\alpha x}\cos\beta x,\; y_2=e^{\alpha x\sin\beta x}$ is new FS.
$\; y_1'=\alpha e^{\alpha x}\cos\beta x+(e^{\alpha x}-\beta\sin\beta x)
=\alpha e^{\alpha x}\cos\beta x-\beta e^{\alpha x}\sin\beta x$
$\; y_2=\alpha e^{\alpha x}\sin\beta x+e^{\alpha x}\beta\cos\beta x
=\alpha e^{\alpha x}\sin\beta x+\beta e^{\alpha x}\cos\beta x$
- $W(y_1, y_2)=\pmatrix{y_1&y_2\\y_1'&y_2'}$
$=\pmatrix{e^{\alpha x}\cos\beta x&e^{\alpha} x\sin\beta x\\
\alpha e^{\alpha x}\cos\beta x-\beta e^{\alpha x}\sin\beta x
&\alpha e^{\alpha x}\sin\beta x+\beta e^{\alpha x}\cos\beta x}\\
=\beta e^{2\alpha x}(\cos^2\beta x+\sin^2\beta x)=\beta e^{2\alpha x}≠0$
- thus, $y_1, y_2$ are FS of (*)
11. 定数係数二階線形同次微分方程式 (I):
- double root: 重根
- >Top Euler's formula:
- $e^{i\theta}=\cos\theta+i\sin\theta$
- $e^{i\pi}=-1$
>Top 12. Constant coefficient secont-order homogeneous DE (II):
- ¶1: $ x''+\omega^2x=0$...(*)
[simple oscillation: $k$=spring constant, $m$=mass of spring, $x_0$=equilibrium point]
- assume FS of (*): $\boxed{x=e^{\lambda t}}$
$→\;x'=\lambda e^{\lambda t}→\;x''=\lambda^2e^{\lambda t}$
- substitute to (*): $\lambda^2e^{\lambda t}+\omega^2e^{\lambda t}
=(\lambda^2+\omega^2)e^{\lambda t}=0$
- $e^{\lambda t}≠0→\;\lambda^2+\omega^2=0$ [characteristic eq]
$→\;\lambda=±i\omega$
- $\therefore\; x=C_1e^{\lambda_1t}+C_2e^{\lambda_2t}
=C_1e^{i\omega t}+C_2e^{-i\omega t}
$
$x=C_1(\cos\omega t+i\sin\omega t)+C_2(\cos\omega t-i\sin\omega t)
=(C_1+C_2)\cos\omega t+i(C_1-C_2)\sin\omega t$
- let: $C_1=\frac{1}{2}(A_1+iA_2),\; C_2=\frac{1}{2}(A_1-iA_2)$: [$x$: real number]
$→\; x=A_1\cos\omega t+A_2\sin\omega t$
- let: $A=\sqrt{A_1^2+A_2^2},\; \cos\alpha=\frac{A_1}{A},\; \sin\alpha
=-\frac{A_2}{A}\;$ [$A_1, A_2$ :constant]
$→\; x=A(\frac{A_1}{A}\cos\omega t+\frac{A_2}{A}\sin\omega t)=A(\cos\omega t\cos\alpha-\sin\omega t\sin\alpha)=
A\cos(\omega t+\alpha)$
- physically:
$→\; v=\frac{dx}{dt}=-A\omega\sin(\omega t+\alpha)$
$→\; a=\frac{d^2x}{dt^2}=-A\omega^2\cos(\omega t+\alpha)$■
- ¶2: $y''+3y'+2y=0$...(*)
- assume one of the solutions:$\; y_1=e^{\lambda x}
\;→y_1'=\lambda e^{\lambda x}\;→y_1''=\lambda^3e^{\lambda x}$
$→\lambda^2(e^{\lambda x}+3\lambda e^{\lambda x}+2e^{\lambda x})=0$
$→e^{\lambda x}(\lambda^2+3\lambda)+2)=0$
$e^{\lambda x}>0\;→(\lambda^2+3\lambda)+2)=0$ [characteristic eq.]
- $D=9-8>0$ above (*) has two real root.
$(\lambda+2)(\lambda+1)=0\;→\lambda=-2, -1$
- $\therefore \;y_1=e^{-2},\; y_2=e^{-1}$ [FS]
$\;→ y=C_1e^{-2}+C_2e^{-1}$ [GS]
- ¶3: $y''-4y'+4y=0$...(*)
- assume one of the solutions:$\; y_1=e^{\lambda x}
\;→y_1'=\lambda e^{\lambda x}\;→y_1''=\lambda^3e^{\lambda x}$
$→\lambda^2(e^{\lambda x}-4\lambda e^{\lambda x}+4e^{\lambda x})=0$
$→e^{\lambda x}(\lambda^2-4\lambda)+4)=0$
$e^{\lambda x}>0\;→(\lambda^2-4\lambda)+4=0$ [characteristic eq.]
- $D=16-16=0$ above (*) has double root.
$(\lambda-2)^2=0\;→\lambda=2$
- $\therefore \;y_1=e^{2x},\;$$ y_2=xe^{2x}$ [FS]
$\;→ y=C_1e^2+C_2xe^2=(C_1+C_2x)e^{2x}$ [GS]
- ¶4: $y''-2y'+5y=0$...(*)
- assume one of the solutions:$\; y_1=e^{\lambda x}
\;→y_1'=\lambda e^{\lambda x}\;→y_1''=\lambda^3e^{\lambda x}$
$→\lambda^2(e^{\lambda x}-2\lambda e^{\lambda x}+5e^{\lambda x})=0$
$→e^{\lambda x}(\lambda^2-2\lambda)+5)=0$
$e^{\lambda x}>0\;→(\lambda^2-2\lambda)+5=0$ [characteristic eq.]
- $D=4-20<0$ above (*) has two imaginary root.
$→\lambda=1±\sqrt{-4}=1±2i$
- $\therefore \;y_1=e^{\alpha x}\cos\beta x,\; y_2=e^{\alpha x}\sin\beta x$ [FS]
$\;→ y_1=e^x\cos 2x,\; y_2=e^x\sin 2x$
$y=e^{\alpha x}(C_3\cos\beta x+C_4\sin\beta x)$$=e^x(C_3\cos 2x+C_4\sin 2x)$ [GS]
12. 定数係数二階線形同次微分方程式 (II):
- characteristic eq.: 特定方程式
- fundamental solution: 基本解
>Top 13. Constant coefficient second-order linear nonhomogeneous DE (I):
-
$\frac{d^2y}{dx^2}+a\frac{dy}{dx}+by=r(x)$...(*)
- GS of (*) is: $\; y=y_0+C_1y_1+C_2y_2\;$ [SS$(y_0)+\mathrm{GS}_0(y_1, y_2)$]
- assume SS of (*) as: $\boxed{y_0=C_1(x)y_1+C_2(x)y_2}$ [variation of constants]
$y_0'=(C_1'(x)y_1+C_1y_1')+(C_2'(x)y_2+C_2(x)y_2')$
$=(C_1'(x)y_1+C_2'(x)y_2)+(C_1(x)y_1'+C_2(x)y_2')$
- pursue solution: $C_1(x), C_2(x)$ of $C_1'(x)y_1+C_2'(x)y_2=0$...(**)
- then, $y_0'=C_1(x)y_1'+C_2(x)y_2'$
$→\; y_0''=(C_1'(x)y_1'+C_1(x)y_1'')+(C_2'(x)y_2'+C_2(x)y_2'')$
$=(C_1(x)y_1''+C_2y_2'')+(C_1'(x)y_1'+C_2'y_2')$
- substitute for (*):
$(C_1(x)y_1''+C_2y_2''+C_1'(x)y_1'+C_2'y_2')
+a(C_1(x)y_1'+C_2(x)y_2')
+b(C_1'(x)y_1+C_2'(x)y_2)=r(x)$
$→\; C_1(x)(y_1''+ay_1'+by_1)
+C_2(x)(y_2''+ay_2'+by_2)
+C_1'(x)y_1'+C_2'(x)y_2'=r(x)
$
- from FS of associated eq of (*): $\; y_1''+ay_1'+by_1=0,\; y_2''+ay_2'+by_2=0$
$→\;C_1'(x)y_1'+C_2'(x)y_2'=r(x)$
- then, $\cases{y_1C_1'(x)+y_2C_2'(x)=0\\y_1'C_1'(x)+y_2'C_2'(x)=r(x)}$
$→\pmatrix{y_1&y_2\\y_1'&y_2'}\pmatrix{C_1'(x)\\C_2'(x)}\pmatrix{0\\r(x)}$ [sim. eq.]
- when $W(y_1,y_2)≠0\;→\pmatrix{y_1&y_2\\y_1'&-y_2'}^{-1}
=\frac{1}{W(y_2,y_2)}\pmatrix{y_2'&-y_2\\-y_1'&y_1}$
$→\;\pmatrix{C_1'(x)\\C_2'(x)}=\frac{1}{W(y_2,y_2)}\pmatrix{y_2'&-y_2\\-y_1'&y_1}
\pmatrix{0\\r(x)}=\frac{1}{W(y_2,y_2)}\pmatrix{-y_2r(x)\\y_1r(x)}$
- $\therefore \;C_1'(x)=-\frac{y_2r(x)}{W(y_1,y_2)},\; C_2'(x)=\frac{y_1r(x)}{W(y_1,y_2)}$
$→\;C_1(x)=-\int \frac{y_2r(x)}{W(y_1,y_2)}dx,\;
C_2(x)=\int \frac{y_1r(x)}{W(y_1,y_2)}dx$
- SS: $y_0=C_1(x)y_1+C_2(x)y_2$
$\boxed{y_0=-y_1\int \frac{y_2r(x)}{W(y_1,y_2)}dx
+y_2\int \frac{y_1r(x)}{W(y_1,y_2)}dx}$
- then, GS is: $y=C_1y_1+C_2y_2+y_0$
$\boxed{y=C_1y_1+C_2y_2-y_1\int \frac{y_2r(x)}{W(y_1,y_2)}dx
+y_2\int \frac{y_1r(x)}{W(y_1,y_2)}dx}$
- ¶1: $y''+3y'+2y=e^{-2x}\cos x$...(*) [solve GS]
- $y''+3y'+2y=0\;$...[**] [associated eq; solve FS, GS_0]
- assume one of solution: $\boxed{y=e^{\lambda x}}$
$→\;y'=\lambda e^{\lambda x},\; y''=\lambda^2 e^{\lambda x}$
$→\;\lambda^2e^{\lambda x}+3\lambda e^{\lambda x}+2e^{\lambda x}$
$→\;(\lambda^2+3\lambda+2)e^{\lambda x}=0$
$e^{\lambda x}>0→\;(\lambda^2+3\lambda+2)=0$
$D=9-8>0$ [two real root]
- $(\lambda+2)(\lambda+1)=0→\;\lambda=-2, -1$
$→\; y_1=e^{-2x},\; y_2=e^{-x}$ [FS]
$→\; y=C_1e^{-2x}+C_2e^{-x}$ [GS_0]
- pursue SS $y_0$ of (*):
formula: $\boxed{y_0=-y_1\int \frac{y_2r(x)}{W(y_1,y_2)}
+y_2\int \frac{y_1r(x)}{W(y_1,y_2)}}$
$W=\pmatrix{y_1&y_2\\y_1'&y_2'}=y_1y_2'-y_1'y_2
=(e^{-2x})(-e^{-x})-(-2e^{-2x})(e^{-x})=e^{-3x}$
$y_0=-e^{-2x}\int \frac{e^{-x}e^{-2x}\cos x}{e^{-3x}}
+e^{-x}\int \frac{e^{-2x}e^{-2x}\cos x}{e^{-3x}}$
$y_0=-e^{-2x}\int \cos xdx+e^{-x}\int e^{-x}\cos xdx$
here: $\int\cos xdx=\sin x,\;
\int e^{-x}\cos xdx=e^{-x}\sin x-e^{-x}\cos x-\int e^{-x}\cos xdx$
$→\; 2\int e^{-x}\cos xdx=e^{-x}(\sin x-\cos x)$
$→\;\int e^{-x}\cos xdx=\frac{1}{2}e^{-x}(\sin x-\cos x)$
$\therefore\; y_0=-e^{-2x}\sin x+\frac{1}{2}e^{-2x}(\sin x-\cos x)$ [SS; omit C]
- then GS of (*): $y=C_1e^{-2x}+C_2e^{-x}-\frac{1}{2}e^{-2x}(\sin x+\cos x)$
13. 定数係数二階線形非同次微分方程式 (I):
- GS: Eqの一般解
- SS: Eqの特殊解
- GS_0: 同伴Eqの一般解
- variation of constants: 定数変化法
- singular solution: 特異解
- simultaneous eqs.: 連立方程式
- invers matrix: 逆行列
- envelope: 包絡線
- $\pmatrix{a&b\\c&d}^{-1}
=\frac{1}{ad-bc}
\pmatrix{d&-b\\-c&a}
$
- $y’’+ay'+by=r(x)$...(*)
- GS=SS+GS_0
- $y_0=C_1(x)y_1+C_2(x)y_2$
- $y’’+ay'+by=0$...(**) ass.eq
- formula:
- $y''+ay'+by=r(x)$
- $y=C_1y_1+C_2y_2\\
-y_1\int\frac{y_2r(x)}
{W(y_1,y_2)}dx\\
+y_2\int \frac{y_1r(x)}
{W(y_1,y_2)}dx\\$
>Top 14. Constant coefficient second-order linear nonhomogeneous DE (II):
-
$\frac{d^2y}{dx^2}+a\frac{dy}{dx}+by=r(x)$...(*)
- one of solution FS of: $y''+ay'+by=0$...(**)
- let GS ($y_1$) of (*): $\boxed{y=u(x)y_1}$
$→\;y'=u'(x)y_1+u(x)y_1'$
$→\;y''=u''(x)y_1+2u'(x)y_'+u(x)y_1''$
- substitute to (*): $(u''(x)y_1+2u'(x)y_1'+u(x)y_1'')+a(u'(x)y_1+u(x)y_1')+bu(x)y_1=r(x)$
$→\; u(x)(y_1''+ay_1'+by_1)+y_1u''(x)+(2y_1'+ay_1)u'(x)=r(x)$
$substitute to (**):\; y_1''+ay_1'+by_1=0$
$→\; y_1u''(x)+(2y_1'+ay_1)u'(x)=r(x)$
$→\; u''(x)+(\frac{2y_1'}{y_1}+a)u'(x)=\frac{r(x)}{y_1}→\;u'(x)=p→\;u''=p'$
- then: $p'+(\frac{2y_1'}{y_1}+a)p=\frac{r(x)}{y_1}$...(3)
let: $p_0(x)=\frac{2y_1'}{y_1}+a,\; q_0(x)=\frac{r(x)}{y_1}$
(3) is $\;\boxed{p'+p_0(x)p=q_0(x)}$ [1st nonhomo LDE]
- $p=\boxed{e^{-\int p_0(x)dx}\left(\int q_0(x)e^{\int p_0(x)dx}dx+C_1\right)}$
- $u'(x)=p→\;u(x)=\int p$
substitute to $y=u(x)y_1$
- ¶1. Solve GS of: $y''+3y'+2y=e^{-2x}\cos x$...(*) has one of GS ($y_1=e^{-2x}$)
- assume: $\boxed{y=u(x)y_1}$
one of GS of (*)$y=u(x)e^{-2x}→\;y'=u'(x)e^{-2x}-2u(x)e^{-2x}$
$→\;y''=u''(x)e^{-2x}-2u'(x)e^{-2x}-2u'(x)e^{-2x}+4u(x)e^{-2x}$
$=(u''(x)-4u'(x)+4u(x))e^{-2x}$
- substitute (*): $(u''(x)-4u'(x)+4u(x))e^{-2x}+(u'(x)e^{-2x}-2u(x))3e^{-2x}
+2u(x)e^{-2x}=e^{-2x}\cos x$
$→\;u''(x)e^{-2x}-u'(x)e^{-2x}=e^{-2x}\cos x$
$e^{-2x}>0→\;u''(x)-u'(x)=\cos x$
- let $u'(x)=p→\;u''(x)=p'→\; p'-p=\cos x$
- substitue formula of 1LDE: $p(x)=-1, q(x)\cos x$
$p=e^{\int dx}\left(\int \cos xe^{-\int dx}dx+C_1\right)
=e^x(\int e^{-x}\cos xdx+C_1)$
- here: $\; \int e^{-x}\cos xdx=e^{-x}\sin x-e^{-x}\cos x-\int e^{-x}\cos x$
$→\;2\int e^{-x}\cos xdx=e^{-x}(\sin x-\cos x)$
- $p=\frac{1}{2}(\sin x-\cos x)+C_1e^{x}$
- $u'(x)=\frac{1}{2}\sin x-\frac{1}{2}\cos x+C_1e^x$
$→\;u(x)=-\frac{1}{2}\cos x-\frac{1}{2}\sin x+C_1e^x+C_2$
- substitute $y=u(x)e^{-2x}$
$\therefore y=C_1e^{-x}+C_2e^{-2x}-\frac{1}{2}e^{-2x}(\cos x+\sin x)$
14. 定数係数二階線形非同次微分方程式 (II):
>Top 15. Euler's DE (I):
-
$x^2\frac{d^2y}{dx^2}+ax\frac{dy}{dx}+by=0$...(*)
- assume FS of (*): $\boxed{y=x^{\lambda}}$
$
→\;y'=\lambda x^{\lambda-1}→\;y''=\lambda(\lambda-1)x^{\lambda-2}$
- substitute to (*): $x^2\lambda(\lambda-1)x^{\lambda-2}
+ax\lambda x^{\lambda-1}+bx^{\lambda}=0$
$→\;\lambda(\lambda-1)x^{\lambda}+a\lambda x^{\lambda}+bx^{\lambda}=0$
$→\;(\lambda^2+(a-1)\lambda+b)x^{\lambda}=0$
- $x^{\lambda}≠0→\;\lambda^2+(a-1)\lambda+b=0$...(**) [characteristic eq.]
- case of $D=(a-1)^2-4b>0$ [different two real root]
- $y_1=x^{\lambda_1},\; y_2=x^{\lambda_2}$ [FS of (*)]
- $W(y_1,y_2)=\pmatrix{x^{\lambda_1}&x^{\lambda_2}\\
\lambda_1x^{\lambda_1-1}&\lambda_2x^{\lambda_2-1}}
=\lambda_2x^{\lambda_1+\lambda_2-1}
-
\lambda_1x^{\lambda_1+\lambda_2-1}
=(\lambda_2-\lambda_1)x^{\lambda_1+\lambda_2-1}≠0$
- $\boxed{\therefore\; y=C_1x^{\lambda_1}+C_2x^{\lambda_2}}$ [GS of (*)]
- Case of $D=(a-1)^2-4b=0$ [double real root]
- assume: two linear independent solution are
$\boxed{y_1=x^{\lambda_1},\; y_2=u(x)x^{\lambda_1}}$
$→\; y_2'=u'(x)x^{\lambda_1}+\lambda_1u(x)x^{\lambda_1-1}$
$→\; y_2''=u''(x)x^{\lambda_1}+2\lambda_1u'(x)x^{\lambda_-1}
+\lambda_1(\lambda_1-1)
u(x)x^{\lambda_1-2}$
- substitute to (*): $x^2(u''(x)x^{\lambda_1}+2\lambda_1u'(x)x^{\lambda_-1})
+ax(u'(x)x^{\lambda_1}+\lambda_1u(x)x^{\lambda_1-1})
+bu(x)x^{\lambda_1}=0$
$→\;u''(x)x^{\lambda_1+2}+(2\lambda_1+a)u'(x)x^{\lambda_1+1}
+(\lambda_1(\lambda_1-1)+a\lambda_1+b)u(x)x^{\lambda_1}=0$
- from (**)$→\;u''(x)x^{\lambda_1+2}+u'(x)x^{\lambda_1+1}=0$
$u''(x)x+u'(x)=0$
- here let: $u'(x)=p→\;u''(x)=p'→\;p'x+p=0→\;p'=-\frac{1}{x}p$
$→\;\frac{dp}{dx}=-\frac{1}{x}dx→\;\int\frac{1}{p}dp=-\int\frac{1}{x}dx$
$\therefore\;\log|p|=-\log|x|+C=\log C_2-\log x=\log\frac{C_2}{x}$
$\therefore\;\log|p|=\log\frac{C_2}{x}→\;p=±\frac{C_2}{x}$
- $\frac{du(x)}{dx}=±\frac{C_2}{x}→\;u(x)=C_3\int \frac{1}{x}dx
→\;u(x)=C_3\log x+C_4$
let: $C_3=1, C_4=0→\;u(x)=\log x$
- then, $y_1=x^{\lambda_1},\;y_2=u(x)x^{\lambda_1}=x^{\lambda_1}\log x$
- $→\; y=C_1x^{\lambda_1}+C_2x^{\lambda_1}\log x$
$\boxed{\therefore\;y=(C_1+C_2\log x)x^{\lambda_1}}$
- $W(y_1,y_2)=\pmatrix{x^{\lambda_1}&x^{\lambda_1\log x}
\\\lambda_1x^{\lambda_1-1}&(\lambda_1\log x+1)x^{\lambda_1-1}}
=x^{2\lambda_1-1}≠0$
- Case of $D=(a-1)^2-4b<0$ [double imaginary root]$
- here: $\lambda_1=\alpha+i\beta,\;\lambda_2=\alpha-i\beta$
$→\;y_1=x^{\lambda_1}=x^{\alpha+i\beta}=x^{\alpha}x^{i\beta}
=x^{\alpha}e^{i\beta\log x}=x^{\alpha}\bigl(\cos (\beta\log x)+i\sin (\beta\log x)\bigr)$
$y_2=x^{\lambda_2}=x^{\alpha}x^{-i\beta}
=x^{\alpha}(\cos (-\beta\log x)+i\sin (-\beta\log x))\\
=x^{\alpha}\bigl(\cos (\beta\log x)-i\sin (-\beta\log x)\bigr)
$
- let FS newly: $y_1=\frac{1}{2}(x^{\lambda_1}+x^{\lambda_2})
=x^{\alpha}\cos (\beta\log x),\; y_2=\frac{1}{2}(x^{\lambda_1}-x^{\lambda_2})
=x^{\alpha}\sin (\beta\log x)$
- then GS: $y=C_1y_1+C_2y_2
=C_1x^{\alpha}\cos (\beta\log x)+C_2x^{\alpha}\sin (\beta\log x)$
- $\boxed{\therefore\; y=x^{\alpha}\bigl(C_1\cos (\beta\log x)+C_2\sin (\beta\log x)\bigr)}$
- $W(y_1,y_2)=\beta x^{2\alpha-1}\bigl(\cos^2(\beta\log x)+\sin^2(\beta\log x)\bigr)
=\beta x^{2\alpha-1}≠0$ [linear independent]
15. オイラーの微分方程式 (I):
>Top 16. Euler'S DE (II):
-
$x^2\frac{d^2y}{dx^2}+ax\frac{dy}{dx}+by=0$...(*)
- let: $\boxed{x=e^t}→\; t=\log x→\;\frac{dt}{dx}=\frac{1}{x},
→\;\frac{dy}{dx}=\frac{dt}{dx}=\frac{1}{x}\frac{dy}{dt}$
$\frac{d^2}{dx^2}=-\frac{1}{x^2}\frac{dy}{dt}+\frac{1}{x^2}\frac{d^2}{dt^2}
=\frac{1}{x^2}(\frac{d^2}{dt^2}-\frac{dy}{dt})
$
- substitute to (*): $x^2\frac{1}{x^2}(\frac{d^2}{dt^2}-\frac{dy}{dt})
+ax\frac{1}{x}\frac{dy}{dt}+by=0
$
$→\;\frac{d^2y}{dt^2}-\frac{dy}{dt}+a\frac{dy}{dt}+by=0$
$→\;\frac{d^2y}{dt^2}+(a-1)\frac{dy}{dt}+by=0$...(**)
- assume either FS: $\boxed{y=e^{\lambda t}}$
- substitute to (**): $\lambda^2e^{\lambda t}+(a-1)\lambda e^{\lambda t}
+be^{\lambda t}=0$
$→\;(\lambda^2+(a-1)\lambda+b)e^{\lambda t}=0$
$e^{\lambda t}≠0→\;(\lambda^2+(a-1)\lambda+b)=0$...(*3) [characteristic eq]
- D>0: $y_1=e^{},\; y_2=e^{}$ [FS of (**)]
$→\; x=e^t→\;e^{\lambda\log x}=e^{\log x^{\lambda}}=x^{\lambda}$
$y_1=e^{\lambda_1\log x},\;y_2=e^{\lambda_2\log x}$
$\boxed{y_1=x^{\lambda_1},\;y_2=x^{\lambda_2}}$
$\therefore\;y=C_1x^{\lambda_1}+C_2x^{\lambda_2}$ [GS of (*)]
- D=0: $y_1=e^{\lambda_1 t}$, assume $\boxed{y_2=te^{\lambda_1 t}}$ [another BS]
$x=e^t→\;t=log x→\;y_1=x^{\lambda_1},\; y_2=(\log x)e^{\lambda_1\log x}
=x^{\lambda_1}\log x
$
$\therefore\;\boxed{ y=C_1x^{\lambda_1}+C_2x^{\lambda_1}\log x}$
- D<0: $y_1=e^{\lambda_1 t},\; y_2=e^{\lambda_2 t}$ [FS of (**)]
$\lambda_1=\alpha+i\beta,\; \lambda_2=\alpha-i\beta$
$→\;y_1=e^{\alpha t}\cos\beta t,\ y_2=e^{\alpha t}\sin\beta t$
$x=e^t→\;t=\log x→\;y_1=x^{\alpha}\cos (\beta\log x),
\;y_2=x^{\alpha}\sin (\beta\log x)$
$→\; \boxed{y=C_1x^{\alpha}\cos (\beta\log x)+C_2x^{\alpha}\sin (\beta\log x)}$
16. オイラーの微分方程式 (II):
>Top 17. Euler'S DE (III):
-
$x^2\frac{d^2y}{dx^2}+ax\frac{dy}{dx}+by=0$...(*)
- ¶1.: Solve GS: $x^2y''+4xy'+2y=0$
- assume FS: $\boxed{y=x^{\lambda}}$
$→\; y'=\lambda x^{\lambda-1},\; y''=\lambda(\lambda-1)x^{\lambda-2}$
- substitute to (*): $\lambda(\lambda-1)x^{\lambda}
+4\lambda x^{\lambda}+2x^{\lambda}=0$
$→\; (\lambda^2+3\lambda+2)x^{\lambda}=0$
$→\;x^{\lambda}≠0→\; (\lambda+1)(\lambda+2)=0→\;\lambda=-2, -1$
- $\therefore\; y_1=x^{-2},\;y_2=x^{-1}$
$\boxed{y=C_1x^{-2}+C_2x^{-1}}$ [GS]
- ¶2.: Solve GS: $x^2y''-3xy'+4y=0$
- assume FS: $\boxed{y=x^{\lambda}}$
$→\; y'=\lambda x^{\lambda-1},\; y''=\lambda(\lambda-1)x^{\lambda-2}$
- substitute to (*): $\lambda(\lambda-1)x^{\lambda}
-3\lambda x^{\lambda}+4x^{\lambda}=0$
$→\; (\lambda^2-4\lambda+4)x^{\lambda}=0$
$→\;x^{\lambda}≠0→\; (\lambda-2)^2=0→\;\lambda=2$
- $y_1=x^{\lambda_1},\;$ assume: $y_2=x^{\lambda_1}\log x$
$\boxed{y=C_1x^{2}+C_2x^{2}\log x}$ [GS]
- ¶3.: Solve GS: $x^2y''-xy'+5y=0$
- assume FS: $\boxed{y=x^{\lambda}}$
$→\; y'=\lambda x^{\lambda-1},\; y''=\lambda(\lambda-1)x^{\lambda-2}$
- substitute to (*): $\lambda(\lambda-1)x^{\lambda}
-\lambda x^{\lambda}+5x^{\lambda}=0$
- $→\; (\lambda^2-2\lambda+5)x^{\lambda}=0$
$→\;x^{\lambda}≠0→\; (\lambda^2-2\lambda+5)=0$
- D=4-20<0: two imaginary root: $\lambda=1±2i→\;\alpha=1,\;\beta=2$
- $y_1=x-{\alpha}\cos (\beta\log x)=x\cos(2\log x),
\;y_2=x\sin (2\log x)$ [FS]
- $\therefore\; \boxed{y=x\bigl(C_1\cos (2\log x)+C_2\sin (s\log x)\bigr)}$ [GS]
- formula:
- D>0: $\boxed{ y_1=e^{\lambda_1t}=x^{\lambda_1},
\;y_2=e^{\lambda_2t}=x^{\lambda_2}}$
- D=0: $\boxed{ y_1=e^{\lambda_1t}=x^{\lambda_1},
\;y_2=te^{\lambda_1t}=x^{\lambda_1}\log x}$
- D<0: $\boxed{ y_1=e^{\alpha t}\cos\beta t=x^{\alpha}\cos (\beta\log x),
\;y_2=e^{\alpha t}\sin\beta t=x^{\alpha}\sin (\beta\log x)}$
17. オイラーの微分方程式 (III):
>Top 18. Differential operator: $\frac{dy}{dx}=Dy$
- $\frac{dy}{dx}=Dy, \frac{d^2y}{dx^2}=D^2y, \frac{d^n}{dx^n}=D^ny$
- $y^{n}+a_1y^{n-1}+a_2y^{n-2}+\dots+a_{n-1}y'+a_ny=R(x)$...(*)
- $y^{n}+a_1y^{n-1}+a_2y^{n-2}+\dots+a_{n-1}y'+a_ny=0\;$ [associated equation]
- $\phi(\lambda)=\lambda^{n}+a_1\lambda^{n-1}+a_2\lambda^{n-2}+\dots+a_{n-1}\lambda'+a_n \; [y=e^{\lambda x}; \phi(\lambda)=$ characteristic eq.]
- $\phi(D)=D^n+a_1D^{n-1}+a_2D^{n-2}+\dots+a_{n-1}D+a_n$
- thus: the above (*) is rewriten:
$\phi(D)y=(\phi(D)=D^n+a_1D^{n-1}+a_2D^{n-2}+\dots+a_{n-1}D+a_n)y=R(x)$
[nth LDE]
- $y=\frac{1}{\phi(D)}R(x)$ [this can sastify GS of nth LDE]
- Inverse operator: $\frac{1}{D}$
- $D^0=1,\; D^n=\frac{d^n}{dx^n}$
- $(D^m±D^n)f(x)=D^mf(x)±D^nf(x),\;D^m(df(x))=dD^mf(x)$
- $D^m(D^nf(x))=D^n(D^mf(x))=D^{m+n}f(x)$
- $\frac{1}{D}f(x)=\int f(x)dx,\; \frac{1}{D^n}f(x)=\int\int\dots\int f(x)(dx)^n$
- ¶1: $(D^2+D)(x^3+2x^2)$
- $(D^2+D)f(x)=D^2f(x)+Df(x)=D^2(x^3+2x^2)+D(x^3+2x^2)\\
=6x+4+3x^2+4x=3x^2+10x+4$
- ¶2: $\frac{1}{D}(x^3+2x^2)=\int (x^3+2x^2)dx=\frac{1}{4}x^4+\frac{2}{3}x^3+C$
- consider: $\frac{1}{D-\alpha}f(x)=y$
- $f(x)=y(D-\alpha)=y'-\alpha y$ [1st LDE]
- $y=e^{-\int p(x)dx}(\int q(x)e^{\int p(x)dx}+C)\;$ [solution of 1LDE $y'+p(x)y=q(x)$]
$y=e^{\int \alpha dx}\int f(x)e^{-\int \alpha dx}dx$
$\boxed{\therefore y=e^{\alpha x}\int f(x)e^{-\alpha x}dx=\frac{1}{D-\alpha}f(x)}$
- consider: $\frac{1}{(D-\alpha_2)(D-\alpha_1)}f(x)
=\frac{1}{D-\alpha_2}\frac{1}{D-\alpha_1}f(x)
=\frac{1}{D-\alpha_2}e^{\alpha_1 x}\int e^{-\alpha_1 x}f(x)dx\\
=e^{\alpha_2 x}\int e^{-\alpha_2 x}(e^{\alpha_1 x}\int e^{-\alpha_1 x}f(x)dx)
dx$
- hence: $\frac{1}{(D-\alpha_n)\dots (D-\alpha_2)(D-\alpha_1)}f(x)
=e^{\alpha_nx\int} e^{-\alpha_nx}・\dots・e^{\alpha_2x}\int e^{-\alpha_2x}
・e^{\alpha_1x}\int e^{-\alpha_1x}・f(x)(dx)^n$
- consider: $De^{\alpha x}=\frac{d}{dx}e^{\alpha x}=\alpha e^{\alpha x},\;
D^2e^{\alpha x}=\alpha^2x^{\alpha x},\;
→D^ne^{\alpha x}=\frac{d^n}{dx^n}e^{\alpha x}=\alpha^ne^{\alpha x}$
- $\phi(D)=D^n+a_1D^{n-1}+a_2D^{n-2}+\dots+a_{n-1}D+a_n$
- $\phi(D)e^{\alpha x}=D^ne^{\alpha x}+a_1D^{n-1}e^{\alpha x}
+a_2D^{n-2}e^{\alpha x}+\dots+a_{n-1}De^{\alpha x}+a_ne^{\alpha x}$
- $\phi(D)e^{\alpha x}=\alpha^ne^{\alpha x}+a_1\alpha^{n-1}e^{\alpha x}
+a_2\alpha^{n-2}e^{\alpha x}+\dots+a_{n-1}\alpha e^{\alpha x}+a_ne^{\alpha x}\\
=(\alpha^n+a_1\alpha^{n-1}+\dots+\alpha_{n-1}\alpha+a_n)e^{\alpha x}
=\phi(\alpha)
e^{\alpha x}$
- $\therefore \phi(D)e^{\alpha x}=\phi(\alpha)e^{\alpha x}$
- $→ e^{\alpha x}=\frac{1}{\phi(D)}(\phi(D)e^{\alpha x})
=\frac{1}{\phi(D)}(\phi(\alpha)e^{\alpha x})$
- when $\phi(\alpha)≠0:\; \frac{1}{\phi(D)}e^{\alpha x}
=\frac{1}{\phi(\alpha)}e^{\alpha x}$
- Formula:
-
- $\frac{1}{\phi(D)}e^{\alpha x}=\frac{1}{\phi(\alpha)}e^{\alpha x}$
- $\frac{1}{\phi(D)}(e^{\alpha x}f(x))=e^{\alpha x}\frac{1}{\phi(D+\alpha)}f(x)$
- $\frac{1}{(D-\alpha)^n}e^{\alpha x}=\frac{x^n}{n!}e^{\alpha x}$
- $\frac{1}{\phi(D^2)}\sin\alpha x=\frac{1}{\phi(-\alpha^2)}\sin\alpha x$
- $\frac{1}{\phi(D^2)}\cos\alpha x=\frac{1}{\phi(-\alpha^2)}\cos\alpha x$
- $\frac{1}{D^2+\alpha^2}\sin\alpha x=-\frac{1}{2\alpha}x\cos\alpha x$
- $\frac{1}{D^2+\alpha^2}\cos\alpha x=\frac{1}{2\alpha}x\sin\alpha x$
18. 微分演算子:
- associated equation: 同伴方程式
- characteristic eq: 特定方程式
- differential operator: 微分演算子
- inverse operator: 逆演算子
- Key formula:
- $\boxed{\frac{1}{D-\alpha}f(x)
=e^{\alpha x}\int
e^{-\alpha x}f(x)dx}$
>Top 19. Solution by differential operator:
- ¶1: $y''+3y'+2y=e^{-2x}\cos x$...(*)
- $(D^2+3D+2)y=e^{-2x}\cos x$
- $(D+2)(D+1)y=e^{-2x}\cos x$
- consider SS $y_0$ of $y=\frac{1}{(D+2)(D+1)}e^{-2x}\cos x$
$y_0=\frac{1}{(D+1)}\frac{1}{(D+2)}e^{-2x}\cos x
=
\frac{1}{(D+1)}(e^{-2x}\frac{1}{D}\cos x)\; [\alpha=-2]$
$=\frac{1}{(D+1)}e^{-2x}\sin x=e^{-x}\frac{1}{D}e^{-x}\sin x
=e^{-x}\int e^{-x}\sin x
;$
- here: $\int e^{-x}\sin xdx=-e^{-x}\cos x-e^{-x}\sin x-\int e^{-x}\sin xdx$
$→ 2\int e^{-x}\sin xdx=-e^{-x}\cos x-e^{-x}\sin x$
$\therefore \int e^{-x}\sin xdx=-\frac{1}{2}e^{-x}(\cos x+\sin x)$
- hence: $y_0=\frac{1}{(D+2)(D+1)}e^{-2x}\cos x=e^{-x}\int e^{-x}\sin x$
$=e^{-x}(-\frac{1}{2}e^{-x}(\cos x+\sin x))
=-\frac{1}{2}e^{-2x}(\cos x+\sin x)$ [SS]
- $y''+3y'+2y=0\;$ [associated eq.]
- $\lambda^2+3\lambda+2=(\lambda+2)(\lambda+1)=0\;→\lambda=-1, -2s$
$\;→y_1=e^{-1}, y_2=e^{-2x}$ [fundamental solution]
- $\therefore GS of (*)$ [GS=FS+SS]
$y=C_1e^{-x}+C_2e^{-2x}-\frac{1}{2}e^{-2x}(\cos x+\sin x)$ [GS]■
19. 微分演算子による解法:
- fundamental solution:基本解
- characteristic equation: 特性方程式
- $\frac{1}{\phi(D)}(e^{\alpha x}f(x))=e^{\alpha x}\frac{1}{\phi(D+\alpha)}f(x)$
- >Top 部分積分, Partial integration
- $\int fg'dx=fg-\int f'gdx$
>Top 20. Series Expansiton:
- ¶1.: $y'-2y=0$ [solve by series expansion]
- $y=a_0+a_1x+a_2x^2+\dots \;→y'=a_1+2a_2x'+3a_3x^{(2)}+\dots$
- $(a_1+2a_2x'+3a_3x^{(2)}+\dots)-2(a_0+a_1x+a_2x^2+\dots)=0$
- $\displaystyle\sum_{k=1}^{\infty}ka_kx^{k-1}
=2\displaystyle\sum_{k=1}^{\infty}a_{k-1}x^{k-1}$
- $→\displaystyle\sum_{k=0}^{\infty}(k+1)a_{k+1}x^k
=2\displaystyle\sum_{k=0}^{\infty}a_kx^k$
- $\therefore (k+1)a_{k+1}=2a_k\;→a_{k+1}=\frac{2}{k+1}a_k$
- $→a_{k+1}=\frac{2}{k+1}\frac{2}{k}a_{k-1}
=
\frac{2}{k+1}\frac{2}{k}\frac{2}{k-1}a_{k-2}
=
\frac{2^{k+1}}{(k+1)!}a_0$
- $\therefore a_k=\frac{2^k}{k!}a_0$
- $→y=\displaystyle\sum_{k=0}^{\infty}\frac{2^k}{k!}a_0x^k
=a_0\bigl(1+\frac{2x}{1!}+\frac{(2x)^2}{2!}+\frac{(2x)^3}{3!}+\dots\bigr)=a_0e^{2x}
$...(1)
- $y'-2y=0\;$ [separable eq.]
$\frac{dy}{dx}=2x \;→\frac{1}{dy}dy=dx\;→\frac{1}{2}\int \frac{1}{y}dy=\int dx$
$\therefore \;\frac{1}{2}\log|y|=x+C\;→\log|y|=2x+2C\;→y=±e^{2x+C=}=Ce^{2x}$...(2)
- $\therefore (1)=(2)$
- Re: Second-order LDE: $y''+p(x)y'+q(x)y=0$...(*)
- if above (*) is extendable by Taylor development at $x=\alpha$:
GS of (*) can be in cases: $y=\displaystyle\sum_{k=0}^{\infty} a_k(x-\alpha)^k$
- otherwise if (*) is extendable at $p(x)(x-\alpha)$ and $q(x)(x-\alpha)^2$:
GS of (*) can be in cases:
$y=(x-\alpha)^{\lambda}\displaystyle\sum_{k=0}^{\infty}a_k(x-\alpha)^k$
20. 級数解法:
- series expansition DE: 級数解法
- 2nd order LDE: 2階線形微分方程式
- $e=\displaystyle\lim_{n\to\infty}
\left(1+\frac{1}{n}\right)^n$
- $e=a\; \mathrm{s.t.}
\frac{d}{dx}a^x=a^x$
- $e=\displaystyle\sum_{k=0}^{\infty}
\frac{1}{k!}$
>Top 21. XXXX:
21. :
Comment
- Problems of DE: 1) there are several ways of solution of DE, 2)the formula is lengthy and complicated, 3) but DE is still limited in being solvable.
- But DE clearly can describe physical change or movement of things, and various economical phenomena.
- Such complixity makes it difficult to learn DE at an early stage of education, notwithstanding it is important to know the essence of modern spirit.
- The idea of people who do not learn DE still remains in 16C -what a pity.
- 微分方程式の問題点は、1) 解法が幾つもある、 2) 公式が長くて複雑、3) それでも解けない問題がある。
- 微分方程式は、物事の物理的な変化や運動や様々な経済的な現象を明確に記述できる。
- このように微分方程式は、近代精神の真髄を学ぶには重要であるにもかかわらず、その複雑性ゆえに教育の初期段階での微分方程式の学習を困難にしている。
- この微分方程式を学ばない人は、その思考は16世紀に留まったままでいる。残念だ。
$\boxed{e^{\int p(x)dx}}$ |
Memorandum of Differential Equations |
Cat: SCI |
compiled by Kanzo Kobayashi from various sources |
20606u |
Title |
Memorandum of Differential Equations |
微分方程式メモ |
|
Index |
|
||
Tag |
; ; ; Bernoulli DE; Differential formula; Differential operator; Euler's formula; Exact DE; First-order LDE; ; Homogeneous function; Integral formula; LDE; Partial integration; Riccati DE; Second-order LDE; Separable equation; Simply connected area; Wronskian; ; | ||
Why |
|
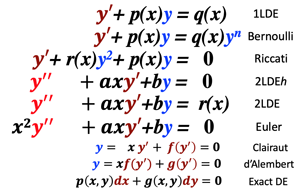 |
|
Name of DE |
Format of DE |
Formula Summary |
>Top変数分離型 |
$y'=f(x)g(y)$ |
0. Formula:
|
| 同次形 | $y'=f(\frac{y}{x})$ |
|
| 1-LDE | $y'+p(x)y=q(x)$ |
|
| Bernoulli DE | $y'+p(x)y=q(x)y^n$ |
|
| Riccati DE | $y'+r(x)y^2+p(x)y=q(x)$ |
|
| Exact DE | $p(x,y)dx+q(x,y)dy=0$ |
|
| Clairaut DE | $y=xy'+f(y')=0$ |
|
| d'Alembert DE | $y=xf(y')+g(y')=0$ |
|
| C-2-LDE (homo ass.eq) | $y''+ay'+by=0$ |
|
| C-2-LDE (nonhomo) | $y''+ay'+by=r(x)$ |
|
| C-2-LDE (nonhomo) w. 1 GS0 only |
$y''+ay'+by=r(x)$ |
|
| Euler DE | $x^2y''+axy'+by=0$ |
|
| Euler DE (II) | $x^2y''+axy'+by=0$ |
|
Original resume |
Remarks |
||
>Top 1. Separable equation:
|
1. 変数分離型:
|
>Top 2. Homogeneous function:
|
2. 同次形:
|
>Top 3. First-order linear differential equation (LDE):
|
3. 一階線形微分方程式:
|
>Top 4. Jakob Bernoulli DE:
|
4. ベルヌーイ微分方程式:<Point>:
|
>Top 5. Yacopo Riccati DE:
|
5. リッカチ微分方程式:
|
>Top 6. Exact DE:
|
6. 完全微分方程式:
|
>Top 7. Exact DE (II) Integrating factor):
|
7. 完全微分方程式 (II): |
>Top 8. Alexis Clairaut DE:
|
8. クレロー微分方程式:
|
>Top 9. d'Alembert's (Lagrange's) DE:
|
9. ダランベール(ラグランジェ)微分方程式: |
>Top 10. Second-order linear differential equation & Wronskian:
|
10. 二階線形微分方程式とロンスキアン:
|
>Top 11. Constant coefficient secont-order homogeneous DE (I):
|
11. 定数係数二階線形同次微分方程式 (I):
|
>Top 12. Constant coefficient secont-order homogeneous DE (II):
|
12. 定数係数二階線形同次微分方程式 (II):
|
>Top 13. Constant coefficient second-order linear nonhomogeneous DE (I):
|
13. 定数係数二階線形非同次微分方程式 (I):
|
>Top 14. Constant coefficient second-order linear nonhomogeneous DE (II):
|
14. 定数係数二階線形非同次微分方程式 (II):
|
>Top 15. Euler's DE (I):
|
15. オイラーの微分方程式 (I): |
>Top 16. Euler'S DE (II):
|
16. オイラーの微分方程式 (II): |
>Top 17. Euler'S DE (III):
|
17. オイラーの微分方程式 (III): |
>Top 18. Differential operator: $\frac{dy}{dx}=Dy$
|
18. 微分演算子:
|
>Top 19. Solution by differential operator:
|
19. 微分演算子による解法:
|
>Top 20. Series Expansiton:
|
20. 級数解法:
|
>Top 21. XXXX: |
21. : |
Comment |
|
|