| Bottom | Home | Article | Bookshelf | Keyword | Author | Oxymoron |

$\frac{dx}{dt}$

Memorandum of Calculus Math
Cat: SCI
Pub: 2020
#2011

compiled by Kanzo Kobayashi
20710u
Title

Calculus Math

微分積分学
Index
  1. Preface:
  2. Important formulas:
  3. Integral using basic formula:
  4. Hyperbolic function:
  5. Integral using exponential-logarithum:
  6. Integral using trigonometry:
  7. Trigonometry to rational function:
  8. Integral by substitution:
  9. Integral by substitution with differential attached:
  10. Integral by parts:
  11. Integral of product of exponential:
  12. Definite integral with absolute value:
  13. Integral of fractional function:
  14. Integral using symmetry:
  15. King property:
  16. Recursive function:
  17. Recurrence relation:
  18. Parametric variable:
  19. Beta function:
  20. Gaussian integral:
  21. l'Hôpital's rule:
  22. Last boss integral:
  1. 序文:
  2. 主要公式(★):
  3. 基本公式による積分(★):
  4. 双曲線関数(H):
  5. 指数関数･対数関数の積分:
  6. 三角関数の積分(▲):
  7. 三角関数の有理関数化(▲):
  8. 置換積分法(♦):
  9. 置換積分法(微分接触型)(✦):
  10. 部分積分法(♥):
  11. 指数関数の積(℮):
  12. 絶対値付の定積分(||):
  13. 分数関数の積分(♣)
  14. 対称性による積分(◐):
  15. キングプロパティ(♠):
  16. 再帰関数(♺):
  17. 漸化式(n-1):
  18. 媒介変数(✔) :
  19. ベータ関数 (β):
  20. ガウス積分 (G):
  21. ロピタルの定理 (Ô):
  22. ラスボス積分:
Why
  • Calculus looks like to trace one's family tree; just as family is a function, and derivatives are descendants, integrals ancestors.
  • Integration seems to be a detective story, whose key resides in details, requiring to have some imagination (and some formula) to solve the answer with pursuing relationship and features of terms of a function.
  • Notation is very important in mathematics, particularly in calculus; and Latex aslo seems to contribute to enhance such notation.
Original resume
Remarks

>Top 0. Preface:

  • Infinitesimal:
    • In 17C, when calculus was discovered by Isaac Newton (1642-1727) and Gottfried Leibniz (1646-1716), lots of criticism occurred. One of the prominent critic was Bishop George Berkeley(1685-1753), wrote, "infinitessimals are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities?"
    • For example such that: let $dx$ be an infinitesimal. Then $2dx$ is also infinitesimal. Therefore $1dx=\frac{1}{2}dx$. Dividing both sides by $dx$, which is not zero; we have a proof that $1=\frac{1}{2}$
    • In 1960's, Abraham Robinson (1918-1974) had shown that it was possible to construct a self-consistent number system that included infinite and infinitesimal numbers; called hyperreal number system which includes the real numbers as a subset.
    • we have at least three levels to the hierarchy: 1) infinities comparable to $H$, 2) finite numbers, and 3) infinitesimal compared to $\frac{1}{H}$
    • Division by zero is undefined. However, we can divide a finite number by an infinitesimal, and get an infinite result.

  • Followings are tips for solving integrals:
    1. ★: Remember important integral formula to lower order of the function.
    2. H: Get wise hyperbolic function:
    3. ℮: Use exponential-logarithum:
    4. ▲: Replace with proper trigonometry to make simpler rationalization.
    5. ♦:Find proper substitution to make simpler function.
    6. ✦: Focus on combination of derivative and its original function:
    7. ♥: Follow integration by parts, selecting proper side of terms to make easier integrals.
    8. ||: Be careful about absolute value
    9. ♣: Consider fractional function
    10. ◐: Be attentive to symmetric function:
    11. ♠: Imagine King property (special case)
    12. ♺: Notice recursive function
    13. n-1: Never forget recurrence relation
    14. ✔: Pay attention to parametric function
    15. β: Picture beta function
    16. G: Recall Gaussian function

0. 序文:

  • pelmanism: 神経衰弱
  • Integral is like a card game Pelmanism:
    ★H℮▲♦✦♥||♣◐♠♺n-1✔βG, and more.

>Top 1. Important formulas (★):

  • Some Calculus formula:
    1. $y=fg\\
      \ln y=\ln(fg)=\ln f+\ln g\\
      \frac{y'}{y}=\frac{f'}{f}
      +\frac{g'}{g}\\
      y'=f'g+fg'$
    2. $y=(\frac{f}{g})$
      $\ln y=\ln\frac{f}{g}
      =\ln f-\ln g\\
      \frac{y'}{y}=\frac{f'}{f}
      -\frac{g'}{g}\\
      y'=\frac{f'}{g}-\frac{fg'}{g^2}
      =\frac{f'g-fg'}{g^2}$
    3. $(e^x)'=e^x$
    4. $(a^x)'=a^x\ln a$
      • $y=a^x\;→\ln y=x\ln a\;→\frac{y'}{y}=\ln a$
    5. $y=(x^x)'$
      $\ln y=x\ln x$
      $\frac{y'}{y}=\ln x+1\\
      y'=y(\ln x+1)=x^x(\ln x+1)$
    6. $(\ln x)'=\frac{1}{x}$
    7. $(\ln y)'=\frac{y'}{y}$
    8. $(\ln_ax)'\\
      =(\frac{\ln x}{\ln a})'\\
      =\frac{1}{\ln a}(\ln x)'\\
      =\frac{1}{x\ln a}$
    9. $(\sin x)'=\cos x$
    10. $(\cos x)'=-\sin x$
    11. $(\tan x)'=\frac{1}{\cos^2x}=\sec^2x$
      • $(\sin x(\cos x)^{-1})'=\cos x(\cos x)^{-1})+\sin x(-1)\cos^2x(-\sin x)
        =1+\tan^2x$
    12. $(\frac{1}{\tan x})'=(\cot x)'=-\frac{1}{\sin^2x}=-\csc^2x$
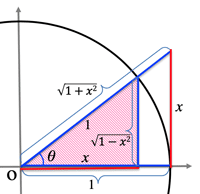
    13. $(\sin^{-1}x)'=\frac{1}{\sqrt{1-x^2}}$
      • $(x)'=(\sin y)'→1=y'\cos y→\cos y=\sqrt{1-\sin^2y}=\sqrt{1-x^2}$
    14. $(\cos^{-1}x)'=-\frac{1}{\sqrt{1-x^2}}$
      • $\cos y=±\sqrt{1-\sin^2y}=±\sqrt{1-x^2};\;(-\frac{\pi}{2}≤y≤\frac{\pi}{2})$
    15. $(\tan^{-1}x)'=\frac{1}{1+x^2}$
    16. $y=x^n\;→y^{(n)}=n!$
    17. $y=\sin x\;→y^{(n)}=\sin(x+\frac{n}{2}\pi)$
    18. $y=\cos x\;→y^{(n)}=\cos(x+\frac{n}{2}\pi)$
    19. $y=e^x\;→y^{(n)}=e^x$
    20. $y=a^x\;→y^{(n)}=a^x(\ln a)^n$
    21. $y=\ln x\;→y^{(n)}=(-1)^{n-1}\frac{(n-1)!}{x^n}$
    22. $y=xe^x\;→y^{(n)}=(x+n)e^x$
    23. $(fg)^{(n)}=\displaystyle\sum_{k=0}^n{}_nC_kf^{(n-k)}g^{(k)}$
      $={}_nC_0f^{(n)}g+{}_nC_1f^{(n-1)}g'+\cdots+{}_nC_{n-1}f'g^{(n-1)}+{}_nC_nfg^{(n)}$
      [Leipniz formula]
    24. $\int \frac{1}{\sqrt{a^2-x^2}}dx=\sin^{-1}\frac{x}{a}+C$
      • let: $x=a\sin t$
    25. $\int \frac{1}{a^2+x^2}dx=\frac{1}{a}\tan^{-1}\frac{x}{a}+C$
      • let: $x=a\tan t$
  • <*Tips>
    1. $a^{\log_ax}=x$
    2. $f(\sin x)\cos x→\sin x=t$
      →dt=\cos xdx
    3. $f(\cos x)\sin x→\cos x=t$
    4. $f(\tan x)\frac{1}{\cos^2x}→\tan x=t→\frac{1}{\cos^2x}dx=dt$
    5. $f(\sin x,\;\cos x)$...(*)
      $→\tan\frac{x}{2}=t$
      $→\sin x=\frac{2t}{1+t^2}$
      $→\cos x=\frac{1-t^2}{1+t^2}$
      $→dt=\frac{1+t^2}{2}dx\;→dx=\frac{2}{1+t^2}dt$
      $\int(*)dx
      =f(\frac{2t}{1+t^2},\;
      \frac{1-t^2}{1+t^2})
      \frac{2}{1+t^2}dt$
    6. $\int\ln xdx→\int 1･\ln xdx$
    7. $\int_0^{\pi}xf(\sin x)dx$
      $=\frac{\pi}{2}\int_0^{\pi}f(\sin x)dx$
  • $\sin^{-1}x=\arcsin x:$
    • $\cos(\arccos x)=x$
  • arcsin

1. 主要公式 (★):

  • Basic: 基本
    $\sin(\frac{\pi}{2}-x)=\cos x$
    $\cos(\frac{\pi}{2}-x)=\sin x$
    $\sin(x+\frac{\pi}{2})=\cos x$
    $\cos(x+\frac{\pi}{2})=-\sin x$
    $\sin(x+\pi)=-\sin x$
    $\cos(x+\pi)=-\cos x$

  • Addition formula: 加法定理
    $\sin(a\pm b)=\sin a\cos b\pm \cos a\sin b$
    $\cos(a\pm b)=\cos a\cos b\mp \sin a\sin b$
    $\tan(a\pm b)=\frac{\tan a\pm\tan b}
    {1\mp\tan a\tan b}$

  • Double angle formula: 倍角
    $\sin 2x=2\sin x\cos x$
    $\cos 2x=\cos^2x-\sin^2x
    =2\cos^2x-1=1-2\sin^2x$
    $\tan 2x=\frac{2\tan x}{1-2\tan^2 x}$

  • Half angle formula: 半角
    $\sin^2x=\frac{1}{2}(1-\cos 2x)$
    $\cos^2x=\frac{1}{2}(1+\cos 2x)
    =\frac{1}{1+\tan^2x} $
    $\tan^2x=\frac{1-\cos 2x}{1+\cos 2x} $

  • Tripple angle formula: ３倍角
    $\sin 3x=3\sin x-4\sin^3x$
    $\cos 3x=4\cos^3x-3\cos x$
    (x=0: 4-3)

  • $(\cos x+i\sin x)^3
    =\cos^3x+3i\cos^2x\sin x$
    $-3\cos x\sin^2x-i\sin^3x$
    $= \cos 3x+i\sin 3x $

  • Product-Sum formula: 積和
    $\sin a\cos b=\frac{1}{2}\bigl(\sin(a+b)
    +\sin(a-b)\bigr)$
    $\sin a\sin b=\frac{1}{2}\bigl(-\cos(a+b)
    +\cos(a-b)\bigr)$
    $\cos a\cos b=\frac{1}{2}\bigl(\cos(a+b)
    +\cos(a-b)\bigr)$

  • Sum-Product formula: 和積
    $\sin a+\sin b=2\sin\frac{a+b}{2}
    \cos\frac{a-b}{s}$
    $\sin a-\sin b=2\cos\frac{a+b}{2}
    \sin\frac{a-b}{s}$
    $\cos a+\cos b=2\cos\frac{a+b}{2}
    \cos\frac{a-b}{2}$
    $\cos a-\cos b=-2\sin\frac{a+b}{2}
    \sin\frac{a-b}{2}$

  • Inverse trigonometric: 逆三角関数
    $(\sin^{-1}x)'=\frac{1}{\sqrt{1-x^2}}$
    $(\cos^{-1}x)'=-\frac{1}{\sqrt{1-x^2}}$
    $(\tan^{-1}x)'=\frac{1}{1+x^2}$

  • $(\ln (\sin x))'=\frac{(\sin x)'}{\sin x}
    =\frac{\cos x}{\sin x}$
    $(\ln |\tan x|)'
    =\frac{1}{\tan x}\frac{1}{\cos^2x}$
    $=\frac{1}{\sin x\cos x}$

  • $\cos(\sin^{-1}x)$
    $ =\sqrt{1-\{\sin (\sin^{-1}x)\}^2}$
    $ =\sqrt{1-x^2}$
  • $\sin(\sin^{-1}x)=\cos(\cos^{-1}x)$
    $=\tan(\tan^{-1}x) =x$
    $\sin(\cos^{-1}x)=\cos(\sin^{-1}x)=$
    $ =\sqrt{1-\{\cos (\cos^{-1}x)\}^2}$
    $ =\sqrt{1-x^2}$
    $\cos(\tan^{-1}x)=\sin(\cot^{-1}x)$
    $=\frac{1}{\sqrt{1+x^2}}$
    $\cos^{-1}x=\sin^{-1}\sqrt{1-x^2}$
    $\tan^{-1}x=\sin^{-1}\frac{x}{\sqrt{x^2+1}}$

 

>Top 2. Integral using Basic formula (★):

  • [Basic $x^a$]:
    1. $\int x^adx=\frac{1}{2}x^{a+1}+C,\;(a≠-1)$
    2. $\int (ax+b)^ndx=\frac{1}{a}\frac{(ax+b)^{n+1}}{n+1}+C$
    3. $\int \frac{1}{\sqrt{1-(ax+b)^2}}dx=\frac{1}{a}\arcsin(ax+b)+C$
    4. $\int \frac{1}{1+(ax+b)^2}dx=\frac{1}{a}\arctan(ax+b)+C$
    5. $\int \sin(ax+b)dx=-\frac{1}{a}\cos(ax+b)+C$
    6. $\int \cos(ax+b)dx=\frac{1}{a}\sin(ax+b)+C$
    7. $\int (1+\tan^2(ax+b))dx=\frac{1}{a}\tan(ax+b)+C$
    8. $\int (1+\cot^2(ax+b))dx=-\frac{1}{a}\cot(ax+b)+C$
    9. $\int \frac{1}{a^2+x^2}dx=\frac{1}{a}\arctan(\frac{1}{a}x)+C$
    10. $\int \frac{1}{a^2+b^2x^2}dx=\frac{1}{ab}\arctan(\frac{b}{a}x)+C$
    11. $\int \frac{1}{\sqrt{a^2-x^2}}dx=\arcsin(\frac{1}{a}x)+C$
    12. $\int \frac{1}{\sqrt{a^2-b^2x^2}}dx=\frac{1}{b}\arcsin(\frac{b}{a}x)+C$
    13. $\int\frac{1}{x}=\ln|x|+C,\;(a=1)$
      1. $\int\frac{1}{x^2}=-\frac{1}{x}+C,\;(a=-2)$
      2. $\int\sqrt{x}=\frac{2}{3}x\sqrt{x}+C,\;(a=\frac{1}{2})$
      3. $\int\frac{1}{\sqrt{x}}=2\sqrt{x}+C,\;(a=-\frac{1}{2})$
    14. $\int \frac{f'}{f}=\ln|f|+C$
    15. $\int f^0g^0=f^0g^{-1}-\int f^1g^{-1}$
      1. $\int f^0g^0=f^0g^{-1}-f^1g^{-2}+\int f^2g^{-2}$

  • [Samples]
    1. ¶$\int \sqrt{\frac{4}{3}x+1}dx$
      from: $\int \sqrt{x}dx=\frac{2}{3}x\sqrt{x}$
      $ =\frac{3}{4}\frac{2}{3}(*)\sqrt{*}+C$
    2. ¶$\int \frac{1}{\sqrt{1-3x}}dx$
      from: $\int \frac{1}{\sqrt{x}}=2\sqrt{x}$
      $ =-\frac{2}{3}\sqrt{1-3x}+C$
    3. ¶$\int \frac{2}{\cos^2(5x-1)}dx$
      from: $\int \frac{1}{\cos^2x}dx=\tan x$
      $=\frac{2}{5}\tan(5x-1)+C$
    4. ¶$\int \frac{1}{\sin^2\frac{x}{2}}dx$
      from: $\int \frac{1}{\sin^2x}=-\frac{1}{\tan x}$
      $=-\frac{2}{\tan \frac{x}{2}}+C$

2. 基本公式による積分 (★):
  • $\int f(ax+b)dx=\frac{1}{a}F(ax+b)+C$

  • General formula:
    • $\displaystyle\lim_{x\to\infty} \sum_{i=1}^n
      f(x_i)\Delta x
      =\int_{a}^{b}f(x)dx$
  • Important areas:
    • $\int_0^{\pi}\sin xdx=2$
    • $\int_0^{\frac{\pi}{2}}
      \sin xdx=1$
    • $\int_0^{\frac{\pi}{2}}
      \cos xdx=1$
  • Area with $y$-axis:
    • $S_y=|\int_{c}^{d}xdy|$

  • Length of a curve:
    • $L=\int_a^b
      \sqrt{1+(f'(x))^2}dx$
  • Volume:
    • $V=\pi\int_a^by^2dx$
  • Surface of 3D object:
    • $S=2\pi\int_a^b
      y\sqrt{1+(y')^2}dx$

>Top 3. Hyperbolic function (H):

  • $\sinh x=\frac{e^x-e^{-x}}{2}$
  • $\cosh x=\frac{e^x+e^{-x}}{2}$
  • $\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
  • $\sinh^{-1}x=\ln(x+\sqrt{x^2+1})$
  • $\cosh^{-1}x=\ln(x±\sqrt{x^2-1})$

  • $\cosh^2x-\sinh^2x=1\; $Cf:$[\cos^2x+\sin^2x=1]$
  • $1-\tanh^2x=\frac{1}{\cosh^2x}\;$Cf:$[1+\tan^2x=\frac{1}{\cos^2x}]$
  • $(\sinh x)'=\cosh x$
    • $=\frac{e^x}{2}-\frac{e^{-x}}{2}(-x)'=\frac{e^x}{2}+\frac{e^{-x}}{2}=\cosh x$
  • $(\cosh x)'=\sinh x\;$Cf:$[(\cos x)'=-\sin x]$
  • $(\tanh x)'=\frac{1}{\cosh^2x}$
  • $\sinh(x±y)=\sinh x\cosh y±\cosh x\sinh y$
  • $\cosh(x±y)=\cosh x\cosh y±\sinh x\sinh y$ (*)
  • $\tanh(x±y)=\frac{\tanh x±\tanh y}{1±\tanh x\tanh y}$ (*)

  • $\int \frac{1}{\sqrt{x^2+a}}dx=\ln(x+\sqrt{x^2+a})+C,\;(a>0)$
  • $\int e^x\sin xdx=\frac{1}{2}e^x(\sin x-\cos x)+C)$
  • $\int e^x\cos xdx=\frac{1}{2}e^x(\sin x+\cos x)+C)$

  • Sigmoid function:
    • $f(x)=\frac{1}{1+e^{-ax}},\;(a>0)$
    • $f'(x)=\frac{ae^{-ax}}{(1+e^{-ax})^2}
      =\frac{a}{1+e^{-ax}}\frac{(1+e^{-ax})-1}{1+e^{-ax}}=af(x)(1-f(x))$
    • $f(x)=\frac{1}{1+e^{-ax}}
      =\displaystyle\frac{1}{2}\frac{2e^{\frac{1}{2}ax}}{e^{\frac{1}{2}ax}+e^{-\frac{1}{2}ax}}
      =\frac{1}{2}(1+\tanh (\frac{1}{2}ax))$

  • Point:
    • $\int \frac{1}{\sqrt{x^2+a^2}}dx,\;\int \sqrt{x^2+a^2}dx$
      • let: x=a\sinh\theta
      • or let: x+\sqrt{x^2+a^2}=t
    • $\int \frac{1}{\sqrt{x^2-a^2}}dx,\;\int \sqrt{x^2-a^2}dx$
      • let: x=a\cosh\theta
      • or let: x+\sqrt{x^2-a^2}=t

  • Sample:
    1. ¶$\frac{1}{\sqrt{1+x^2}}dx$...(*)
      let: $x=\frac{e^t-e^{-t}}{2}→e^t=x+\sqrt{x^2+1}→t=\ln(x+\sqrt{x^2+1})$
      $→dx=\frac{e^t+e^{-t}}{2}dt$
      $=\int \frac{1}{\sqrt{1+\frac{(e^t-e^{-t})^2}{4}}}\frac{e^t+e^{-t}}{2}dt$
      $=\int \frac{1}{\frac{e^t+e^{-t}}{2}}\frac{e^t+e^{-t}}{2}dt=\int dt$
      $=t+C=\ln(xL\sqrt{x^2+1})+C$
      • Cf:$\; y=\sqrt{a+x^2}→x^2-y^2=-1\;$[hyperbola]
        here: $x=\frac{e^t-e^{-t}}{2},\;[=\sinh t]$
        $x=\frac{e^t+e^{-t}}{2},\;[=\cosh t]$
      • (*)=$\int \frac{1}{\sqrt{\sinh^2t+1}}\cosh t=\int dt$
    2. ¶$\int \sqrt{x^2+1}$
      let: $x=\sinh t→dx=\frac{e^t+e^{-t}}{2}dt=\cosh tdt$
      let: $e^{2t}-2xe^t-1=0⇔e^t=x+\sqrt{x^2+1},\;(e^t>0)$
      $⇔t=\ln(x+\sqrt{x^2+1})$
      $=\int \sqrt{\sinh^2t+1}\cosh tdt=\int \cosh^2tdt,\;(\cosh t>0)$
      $ =\int \frac{e^{2t}+e^{-2t}+2}{4}dt$
      $=\frac{e^{2t}-e^{-2t}}{8}+\frac{1}{2}t+C$
    3. ¶$\int_{1}^{2}\sqrt{x^2-1}$
      let: $x=\cosh t→dx=\frac{e^t-e^{-t}}{2}dt=\sinh tdt$
      let: $\cosh a=\frac{e^a+e^{-a}}{2}=2$
      $⇔(e^a)^2-4e^a+1=0⇔e^a=2+\sqrt{3},\;(e^a>1)⇔a=\ln(2+\sqrt{3})$
      $ =\int_{0}^{a}\sqrt{\cosh^2t-1}\sinh tdt=\int_{0}^{a}\sqrt{\sinh^2t}\sinh tdt$
      $=\int_{0}^{a}\sinh^2tdt,\; (0<t<a→\sinh t>0)$
      $=\int_{0}^{a}\frac{e^{2t}-2+e^{-2t}}{4}dt$

3. 双曲線関数 (H):

  • $x=\cosh\theta,\;y=\sinh\theta$
    $→x^2-y^2=1\;$ [hyperbolic]
  • $e^{i\theta}=\cos\theta+i\sin\theta$
    $→\cos\theta
    =\frac{e^{i\theta}+e^{-i\theta}}{2}$
    $→\sin\theta
    =\frac{e^{i\theta}-e^{-i\theta}}{2i}$

>Top 4. Integral using Exponential-Logarithm (e):

  • [Exponential-Logarithm]
    1. $\int e^xdx=e^x+C$
    2. $\int a^x=\frac{a^x}{\ln a}+C$
    3. $\int a^x\ln adx=a^x+C$
    4. $\int\ln xdx=\int x'\ln xdx=x\ln x-x(\ln x)'dx=x\ln x-\int dx$
      $=x\ln x-x+C\;$ [\ln = 1･\ln]
    5. $\int \frac{1}{x\ln a}dx=\ln_ax$

  • [Samples]
    1. ¶$\int s^{-\frac{2}{3}+7}dx$
      from: $\int e^xdx=e^x$
      $=-\frac{3}{2}e^{-\frac{2}{3}+7}+C$
    2. ¶$\int \frac{1}{3x+2}dx=$
      from: $\int \frac{1}{x}dx=\ln |x|$
      $=\frac{1}{3}\ln |3x+2|+C$
    3. ¶$\int 5^{8-\frac{5}{3}x}dx$
      from: $\int a^xdx=\frac{a^x}{\ln a}$
      $=-\frac{3}{5}\frac{5^8-\frac{5}{3}x}{\ln 5}+C$

4. 指数関数・対数関数の積分 (e):
  • $a^{\log_ax}=x$

>Top 5. Integral using Trigonometry (▲):

  • [Trigonometry (▲)]
    1. $\int \sin xdx=-\cos x+C$
    2. $\int \cos xdx=\sin x+C$
    3. $\int\tan xdx=\int\frac{\sin x}{\cos x}dx=-\int\frac{(\cos x)'}{\cos x}dx$
      $=-\ln|\cos x|+C$
    4. $\int\frac{1}{\tan x}=\int\frac{\cos x}{\sin x}dx=\int\frac{(\sin x)'}{\sin x}dx=$
      $=\ln|\sin x|+C$
    5. $\int \frac{1}{\cos^2x}dx=\int \sec^2xdx=\int (1+\tan^2x)dx=\tan x+C$
    6. $\int \csc^2xdx=-\cot x+C$
    7. $\int \frac{1}{\cos^2x}dx=\int \sec^2xdx=\int (1+\tan^2x)dx=\tan x+C$
    8. $\int \frac{1}{\sin^2x}dx=\int \csc^2dx=\int (1+\cot^2x)dx
      =-\frac{1}{\tan x}+C=-\cot x+C$
    9. $\int \tan x\sec xdx=\sec x+C$
    10. $\int \cot x\csc xdx=-\csc x+C$
    11. $\int\frac{1}{x^2+a^2}dx=\frac{1}{a}\tan^{-1}\frac{x}{a}+C,\;(a≠0)$
    12. $\int\frac{1}{\sqrt{x^2-a^2}}dx=\sin^{-1}\frac{x}{a}+C,\;(a>0)$
    13. $\int\frac{1}{\sqrt{x^2+a}}dx=\ln |x+\sqrt{x^2+a}|+C,\;(a≠0)$
    14. $\int x^ndx=\frac{x^{n+1}}{n+1}+C,\;(m≠-1)$

  • [Samples]
    1. ¶$\int \frac{1}{\sin^2x\cos^2x}dx$
      from: $1=\sin^2x+\cos^2x$
      from: $\int \frac{1}{\cos^2x}=-\frac{1}{\tan x}$
      $=\int \frac{\sin^2x+\cos^2x}{\sin^2x\cos^2x}dx
      =\int (\frac{1}{\cos^2x}+\frac{1}{\sin^2x})dx=\tan x-\frac{1}{\tan x}+C$
    2. ¶$\int \sin 2x\cos 2xdx$
      from: $\sin 4x=2\sin 2x\cos 2x$
      $=\int \frac{1}{2}\int \sin 4xdx=\frac{1}{2}(-\frac{1}{4}\cos 4x)+C$
    3. ¶$\int \sin 2x\cos 3xdx$
      from: $\sin a\cos b=\frac{1}{2}(\sin (a+b)+\sin(a-b))$
      $=\frac{1}{2}\int (\sin 5x-\sin x)dx=$
    4. ¶$\int \sin^3xdx$
      from: $\sin 3x=3\sin x-4\sin^3x$
      $ =\frac{1}{4}\int (3\sin x-\sin 3x)dx
      =\frac{1}{4}(-3\cos x+\frac{1}{3}\cos 3x)+C$
    5. ¶$\int \cos^3xdx$
      from: $\cos 3x=-3\cos x-4\cos^3x$
      $=-\frac{1}{4}\int (3\cos x+\cos 3x)dx$
      $=-\frac{1}{4}(3\sin x+\frac{1}{3}\sin 3x)+C$
    6. ¶$\int \tan^3dx$
      let: $\cos x=t\;→-\sin xdx=dt$
      $\int \frac{1-\cos^2x}{\cos^3x}\sin xdx=\int \frac{t^2-1}{t^3}dt$
    7. ¶$\int \cos^4xdx=\int (\cos^2x)^2dx$
      from: $\cos 2x+1=2\cos^2x$
      $ =\frac{1}{4}\int (\cos 2x+1)^2dx$
      $=\frac{1}{4}\int (\cos^22x+2\cos 2x+1)dx$
      from: $\cos 4x+1=2\cos^2 2x$
      $=\frac{1}{4}\int \{\frac{1}{2}(\cos 4x+1)+2\cos 2x+1\}dx$
      $=\frac{1}{4}\int \{\frac{1}{2}\cos 4x+2\cos 2x+\frac{3}{2}\}dx$
    8. ¶$\int \cos^5xdx$
      let: $\sin x=t\;→\cos xdx=dt$
      $ =\int (1-\sin^2x)^2\cos xdx=\int (1-t^2)^2dt$
    9. ¶$\int x\cos^3x$
      from: $\cos 3x=-3\cos x+4\cos^3x$
      $=\frac{1}{4}\int x(\cos 3x+3\cos x)dx$
      $=\frac{1}{4}\{x(\frac{1}{3}\sin 3x+3\sin x)-\int (\frac{1}{3}\sin 3x+3\sin x)dx\}$
    10. ¶$\int \frac{1}{\cos^3x}dx$
      multiply $\cos x:\;→\sin x=t\;→\cos xdx=dt$
      $\int \frac{\cos x}{\cos^4x}=\int \frac{\cos x}{(1-\sin^2x)^2}dx
      =\int \frac{1}{(1-t^2)^2}dt $
      $=\int \frac{1}{(1+t)^2(1-t)^2}dt=\frac{1}{4}\int \{\frac{1}{1+t}+\frac{1}{1-t}+\frac{1}{(1+t)^2}+\frac{1}{(1-t)^2}\}dt=$
    11. ¶$\int \frac{1}{\cos^4x}dx$
      let: $tan x=t\;→\frac{1}{\cos^2x}dx=dt$
    12. ¶$\int \frac{1}{\tan^3x}dx$
      let: \sin x=t\;→\cos xdx=dt
      $=\int \frac{\cos^2x}{\sin^3x}\cos xdx=\int \frac{1-\sin^2x}{\sin^3x}\cos xdx$
      $=\int \frac{1-t^2}{t^3}dt=\int (\frac{1}{t^3}-\frac{1}{t})dt$
      $=-\frac{1}{2}t^2-\ln|t|+C$
    13. ¶$\int \frac{1}{\sin^4x}dx$
      let: $\frac{1}{\tan x}=t\;→-\frac{1}{\sin^2x}dx=dt$
      $=\int (1+\frac{1}{\tan^2x})\frac{1}{\sin^2x}dx=\int(1+t^2)(-dt) $
    14. ¶$\int x\sin x\cos xdx=\frac{1}{2}\int x\sin 2xdx$
      here: $\int x\sin 2x=x(-\frac{1}{2}\cos 2x)-\int (-\frac{1}{2}\cos 2x) dx$
    15. ¶$\int \frac{\sin^3x}{\cos^5x}dx$
      let: $\tan x=t\;→\frac{1}{\cos^2x}dx=dt$
      $=\int \tan^3x\frac{1}{\cos^2x}dx=\int t^3dt$
    16. ¶$\int_{0}^{1}\sqrt{\frac{1-x}{1+x}}dx$
      let: $x=\sin \theta\;→dx=\cos \theta d\theta$
      $=\int_{0}^{\frac{\pi}{2}}$

5. 三角関数の積分 (▲):

  • $\sin(\frac{\pi}{2}-x)=\cos x$
  • $\cos(\frac{\pi}{2}-x)=\sin x$
  • $\tan(\frac{\pi}{2}-x)
    =\frac{\cos x}{\sin x}=\frac{1}{\tan x}$

  • $\cos 2x=2\cos^2 x-1=-2\sin^2 x+1$
    $→2\cos^2x=\cos 2x+1$
  • $\cos^2x=(\cos x-\sin x)(\cos x+\sin x)$
  • $\tan 2x=\frac{2\tan x}{1-tan^2x}$
    $→\tan x-\frac{1}{\tan x}
    =-\frac{2}{tan 2x}$

  • $1+\tan^2x=\frac{1}{\cos^2x}$
  • $1+\frac{1}{\tan^2x}=\frac{1}{\sin^2x}$

  • $\sin (a+b)+\sin (a-b)=2\sin a\cos b$
  • $\sin (a+b)-\sin (a-b)=2\cos a\sin b$
  • $\cos (a+b)+\cos (a-b)=2\cos a\cos b$
  • $\cos (a+b)-\cos (a-b)=-2\sin a\sin b$
  • $\int\sin ax\,dx=-\frac{1}{a}\cos ax$
  • $\int\cos ax\,dx=\frac{1}{a}\sin ax$
  • $\int\frac{1}{\cos^2x}dx=\tan x$
  • $\int\frac{1}{\sin^2x}dx=-\frac{1}{\tan x}$

 

  • Tips:
  • $\frac{1}{(1+t)^2(1-t)^2}
    =\frac{A}{1+t}+\frac{B}{1-t}
    +\frac{C}{(1+t)^2}+\frac{1}{(1-t)^2}$

>Top 6. Trigonometry to Rational function (▲):

  • Rationalization:
    Pattern: $\int \frac{1}{\cos x}dx,\;\int \frac{1}{\sin x}dx$
    →$\int \frac{1}{\cos x}dx=\int \frac{\cos x}{\cos^2x}dx=\int \frac{(\sin x)'}{1-\sin^2 x}dx$ then:
    1. Pattern: $\int f(\sin x)\cos xdx$
      let: $\sin x=t$ $\;→\cos xdx=dt$
    2. Pattern: $\int f(\cos x)\sin xdx$
      let: $\cos x=t$ $\;→-\sin xdx=dt$
    3. Pattern: $\int f(\tan x)\frac{1}{\cos^2x}dx$
      let: $\tan x=t$ $\;→\frac{1}{\cos^2x}dx=dt$
    4. Pattern: $\int \frac{1}{\sqrt{a^2-x^2}}dx$
      let: $x= a\sin t$$\;→dx=a\cos dt$
      • $=\int \frac{a\cos t}{\sqrt{a^2-a^2\sin^2tdt}}
        =\int \frac{a\cos t}{|a\cos t|}dt$
    5. Pattern: $\int \frac{1}{a^2+x^2}dx$
      let: $x=a\tan t$$\;→dx=\frac{a}{\cos^2t}dt$
      • $=\int \frac{1}{a^2+a^2\tan^2t}\frac{a}{\cos^2t}
        =\int \frac{\cos^2t}{a^2}\frac{a}{\cos^2t}dt$
    6. Pattern: $\boxed{f(\sin x,\; \cos x)}$
      $=\int f \bigl(\frac{2t}{1+t^2},\;\frac{1-t^2}{1+t^2}\bigr)\frac{2}{1+t^2}dt$
      let: $\tan\frac{x}{2}=t$
      • $→\sin x=\frac{2t}{1+t^2}$
      • $→\cos x=\frac{1-t^2}{1+t^2}$
      • $→\tan x=\frac{2t}{1-t^2}$
      • $→dx=\frac{2}{1+t^2}dt$
        • $\because\tan x=\frac{2\tan \frac{x}{2}}{1-\tan^2\frac{1}{2}
          }=\frac{2t}{1-t^2}$
        • $→\cos^2\frac{x}{2}=\frac{1}{\tan^2\frac{x}{2}+1}=\frac{1}{1+t^2}$
        • $→\cos x=2\cos^2\frac{1}{2}x-1=\frac{2}{1+t^2}-1=\frac{1-t^2}{1+t^2}$
        • $→\sin x=\tan x\cos x
          =\frac{2t}{1-t^2}\frac{1-t^2}{1+t^2}=\frac{2t}{1+t^2}$
        • $→\frac{dt}{dx}
          =\frac{(\sin\frac{x}{2})'\cos\frac{x}{2}-\sin\frac{x}{2}(\cos\frac{x}{2})'}
          {(\cos\frac{x}{2})^2}=\frac{1}{2}\frac{1}{\frac{1}{1+t^2}}
          =\frac{1+t^2}{2}$
        • or, $\tan\frac{x}{2}=t$
          $ →\frac{1}{2\cos^2\frac{x}{2}}=dt→\frac{1}{2}(1+\tan^2\frac{x}{2})dx
          =dt→dx=\frac{2}{1+t^2}dt$
    7. Pattern: $\boxed{f(\sin^2 x,\; \cos^2 x)}$
      $=\int f \bigl(\frac{t^2}{1+t^2},\;\frac{1}{1+t^2}\bigr)\frac{1}{1+t^2}dt$
      let: $\tan x=t$
      • $→\tan^2 x=t^2$
      • $→\cos^2 x=\frac{1}{\tan^2x+1}=\frac{1}{1+t^2}$
      • $→\sin^2 x=(\tan x\cos x)^2=t^2\frac{1}{1+t^2}=\frac{t^2}{1+t^2}$
      • $→dx=\frac{1}{1+t^2}$
        • $\tan x=t\;→\frac{1}{\cos^2x}dx=dt\;→dx=\cos^2xdt
          =\frac{1}{1+t^2}dt$

  • [Samples]
    1. ¶$\int \frac{1}{x^2+4}dx$
      let: $x=2\tan t$$→dx=\frac{2}{\cos^2t}dt$
      here: $\frac{1}{x^2+4}=\frac{1}{4(\tan^2t+1)}=\frac{1}{4}\cos^2t$
      $→\int \frac{1}{4}\cos^2t\frac{2}{\cos^2t}dt=\frac{1}{2}\int dt$
    2. ¶$\int \frac{1}{x^2-2x+4}dx=\int \frac{1}{(x-1)^2+3}dx$
      let: $x-1=\sqrt{3}\tan t$$\;→dx=\frac{\sqrt{3}}{\cos^2t}dt$
      $=\int \frac{1}{3(\tan^2t+1)}dx=\int \frac{1}{3}\cos^2t\frac{\sqrt{3}}{\cos^2t}dt$
    3. ¶$\int \frac{1}{\cos x}dx$
      let: $x=\tan\frac{t}{2}$
      $=\int \frac{1+t^2}{1-t^2}\frac{2t}{1+t^2}dt=\int \frac{2}{1-t^2}dt$
      $=\int (\frac{1}{1+t}+\frac{1}{1-t})dt=\ln|1+t|-\ln|1-t|+C$
      or: $=\int \frac{\cos x}{\cos^2x}dx=\frac{\cos x}{1-\sin^2x}dx+C$
    4. ¶$\int \frac{1}{\sin x}dx$
      let: $x=\tan\frac{t}{2}$
      $\int \frac{1+t^2}{2t}\frac{2}{1+t^2}dt=\int \frac{1}{t}dt=\ln |t|+C$
      or: $=\int \frac{\sin x}{\sin^2x}dx=\int \frac{\sin x}{1-\cos^2x}dx$
      let: $\cos x=t→-\sin xdx=dt$
      $=-\int \frac{1}{1-t^2}dt=-\frac{1}{2}\int (\frac{1}{1-t}+\frac{1}{1+t})dt+C$
    5. ¶$\int \frac{1}{\sin x+\cos x+1}dx$
      let: $x=\tan\frac{t}{2}$
      $=\int \frac{1}{\frac{2t}{1+t^2}+\frac{1-t^2}{1+t^2}+1}\frac{2}{1+t^2}dt$
      $=\frac{1+t^2}{2(t+1)}\frac{2}{1+t^2}dt=\int \frac{1}{t+1}dt=\ln |t+1|+C$
    6. ¶$\int \frac{\sin x}{\sin x+\cos x}dx$
      let: $x=\tan\frac{t}{2}$
      $=\int \frac{2t}{(2t+1-t^2)}\frac{2}{1+t^2}dt$
      $=-4\int \frac{t}{(t^2+1)(t-1+\sqrt{2})(t-1-\sqrt{2})}dt$
      $=-4\int \bigl\{\frac{At+B}{t^2+1}+\frac{C}{t-1+\sqrt{2}}
      +\frac{D}{t-1-\sqrt{2}}\bigr\}dt\;[A=B=-\frac{1}{4}, C=D=\frac{1}{8}]$
      $=\int \bigl\{\frac{t+1}{t^2+1}-\frac{1}{2(t-1+\sqrt{2})}
      -\frac{1}{2(t-1-\sqrt{2})}\bigr\}dt$
      $=\frac{1}{2}\ln(t^2+1)+\tan^{-1}t-\frac{1}{2}\ln|t^2-2t+1|+C$...(*)
      here: $\tan(\tan^{-1}x)=x;\;\ln=|\frac{2t+(1-t^2)}{1+t^2}|=\ln|\sin x+\cos x|$ (*)=\frac{1}{2}(x-\ln|\sin x+\cos x|)+C
    7. ¶$\int \frac{1}{(1+x^2)^2}$
      let: $x=\tan t$$\;→dx=\frac{1}{\cos^2t}dt$
      $\int \cos^4t\frac{1}{\cos^2t}dt=\int \cos^2dt=\frac{1}{2}\int (1+\cos 2t)dt$
    8. ¶$\int \tan^3xdx$
      let: $x=\tan t$$\;→dx=\frac{1}{1+t^2}dt$
      $=\int t^3\frac{1}{1+t^2}dt=\int (1-\frac{t}{t^2+1})dt
      =\int (t-\frac{1}{2}\frac{2t}{t^2+1})dt $
      $=\frac{1}{2}t^2-\frac{1}{2}\ln (t^2+1)+C$
    9. $\int \frac{1}{x^3+1}dx=\int \frac{1}{(x+1)(x^2-x+1)}
      =\frac{1}{3}\int (\frac{1}{x+1}-\frac{1}{2}\frac{(2x-1)-3}{x^2-x+1})dx$
      here: $\frac{1}{x^2-x+1}=\frac{1}{(x-\frac{1}{2})^2+\frac{3}{4}}
      ＝\frac{4}{3}\cos^2t$
      let: $x-\frac{1}{2}=\frac{\sqrt{3}}{2}\tan t$$→dx=\frac{\sqrt{3}}{2\cos^2t}dt$
      $=\int \frac{4}{3}\cos^2t\frac{\sqrt{3}}{2\cos^2t}dt=\int \frac{2\sqrt{3}}{3}dt$
    10. ¶$\int \frac{\sqrt{\tan x}}{\sin 2x}dx$
      let: $\sqrt{\tan x}=t$$\;→dt=\frac{1}{2\sqrt{\tan x}}\frac{1}{\cos^2x}dx
      =\frac{1}{2t}\frac{1}{\cos^2x}dx$
      $=\int \frac{t}{2\sin x\cos x}2t\cos^2xdt=\int \frac{t^2}{\tan x}dt=t+C$

6. 三角関数の有理関数化 (▲):
  • Tips: Lower order
  1. $\sin x\cos x=\frac{1}{2}\sin 2x$
  2. $\sin^2x=\frac{1}{2}(1-\cos 2x)$
  3. $\cos^2x=\frac{1}{2}(1+\cos 2x)$
  4. $\tan^2x+1=\frac{1}{\cos^2x}$

  5. $\sin^3=\frac{3\sin x-\sin 3x}{4}$
  6. $\cos^3=\frac{3\cos x+\cos 3x}{4}$

  7. $\sin ax\cos bx
    =\frac{1}{2}\{\sin (a+b)x+\sin (a-b)x\}$
  8. $\cos ax\cos bx
    =\frac{1}{2}\{\cos (a+b)x+\cos (a-b)x\}$
  9. $\sin ax\sin bx
    =-\frac{1}{2}\{\cos (a+b)x-\cos (a-b)x\}$

>Top 7. Integration by Substitution (♦):

  • [by Substitution (♦)]
  • [Samples]
    1. ¶$\int x^3(x^2-1)^4dx=\int x^2･x(x^2-1)^4dx$
      $x^2-1=t\;→xdx=\frac{1}{2}dt$
      $=\int (t+1)t^4dt=\frac{1}{2}\int (t^5+t^4)dt$
    2. ¶$\int \frac{2x^3}{(x^2+1)^2}dx=\int \frac{x^2･2x}{(x^2+1)^2}dx$
      $x^2+1=t\;→2xdx=dt$
      $=\int \frac{x^2}{(x^2+1)^2･2xdx}=\int \frac{t-1}{t^2}dt=\int (\frac{1}{t}-\frac{1}{t^2})dt$
    3. ¶$\int_1^2\frac{1}{(2x+1)^2}dx
      =\frac{1}{2}\bigl[-\frac{1}{2x+1}\bigr]_1^2$
    4. ¶$\int \sqrt{\frac{1-x}{1+x}}dx$
      let: $\sqrt{\frac{1-x}{1+x}}=t\;→x=\frac{1-t^2}{1+t^2}\;→dx=
      -\frac{4t}{1+t^2}dt$
      $=\int t(-\frac{4t}{1+t^2})dx=-4\int \frac{t^2}{(1+t^2)^2}dt$
      let $t=\tan\theta\;→dt=\frac{1}{\cos^2\theta}d\theta$
      $=4\int \tan^2\theta\cos^4\theta\frac{1}{\cos^2\theta}d\theta
      =4\int \sin^2\theta d\theta=\int 4\theta\frac{1-\cos 2\theta}{2}d\theta$
    5. ¶$\int \sin(\ln x)dx$
      let: $t=\ln x\;→ x=e^t\;→dx=e^tdt$
      here: $\int e^t\sin tdt=e^t\sin t-\int e^t\cos tdt
      =e^t\sin t-\bigl(e^t\cos t+\int e^t\sin tdt\bigr) $
      $\;→\int e^t\sin tdt=\frac{1}{2}e^t(\sin t-\cos t)+C$

7. 置換積分法 (♦):
  • *Tips:
  • $\int f'(ax+b)dx=\frac{1}{a}f(ax+b)+C$
    [Linear change of variable, 一次式置換型]

>Top 8. Integration by Substitution with differential-attached (✦)

  • [by Substitution with differential-attached (✦)]
  • [Samples]
    1. ¶$\int \frac{e^x-e^{-x}}{e^x+e^{-x}}dx=\int \frac{*'}{*}dx=\ln (*)$
    2. ¶$\int \frac{\cos x}{1-\sin x}dx=-\int \frac{*'}{*}=-\ln (*)$
    3. ¶$\int \frac{2^x}{2^x+1}dx=\frac{1}{\ln 2}\int\frac{*'}{*}$
    4. ¶$\int \frac{1}{\sqrt{x}}(\sqrt{x}+1)dx
      =2\int \frac{\frac{1}{2\sqrt{x}}}{\sqrt{x}+1}=2\int \frac{*'}{*}$
    5. ¶$\int x(x^2+1)^5dx=\frac{1}{2}\int 2x(x^2+1)^5dx
      =\frac{1}{2}\int (*')(*)$
    6. ¶$\int \frac{1}{x^2}(1+\frac{1}{x})^2dx=-\int (*)'(*)^2$
    7. ¶$\int \frac{(\sqrt{x}+1)^5}{\sqrt{x}}dx=2\int (*')(*)^5$
    8. ¶$\int \frac{1}{\tan^2x\sin^2x}dx=-\int (\frac{1}{\tan x})^2(-\frac{1}{\sin^2x})dx
      =\int (*^2)(*') $
    9. ¶$\int x^5\sqrt{x^3+1}dx=$
      let: $x^3+1=t\;→3x^2dx=dt$
      $=\int \frac{1}{3}(t-1)\sqrt{t}dt$
    10. ¶$\int \frac{\ln(ln x)}{x\ln x}dx$
      let: $\ln x=t\;→\frac{1}{x}dx=dt$
      $=\int \frac{\ln t}{t}$, then:$\;\ln t=u\;→\frac{1}{t}dt=du$
      $=\int udu$
    11. ¶$\int \sin x\sin(\cos x)dx$
      let: $\cos x=t\;→-\sin xdx=dt$
      $=\int (-\sin x)\sin(\cos x)dx=-\int -\sin tdt$
    12. ¶$\int \frac{\tan x}{(\tan x-1)^2\cos^2x}dx$
      let: $\tan x-1=t\;→\frac{1}{\cos^2 x}dx=dt$
      $=\frac{t+1}{t^2}$
    13. ¶$\int \frac{e^{3x}}{\sqrt{e^x+1}}dx$
      let: $e^x+1=t\;→e^xdx=dt$
      $\int \frac{(e^x)^2e^x}{\sqrt{e^x+1}}=\int \frac{(t-1)^2}{\sqrt{t}}dt$
    14. ¶$\int \cos x\ln (\sin x)dx$
      let: $\sin x=t\;→\cos xdx=dt$
      $=\int \ln tdt=t\ln t-t+C,\;$ [< Tips]
    15. ¶$\int 3^{x+3^x}dx$
      let: $3^x=t\;→3^x\ln 3dx=dt$
      $=\int \frac{1}{\ln 3}･\ln 3･3^x･3^{3^x}dx=\frac{1}{\ln 3}\int 3^tdt$
    16. ¶$\int \frac{1}{\sqrt{x}\sin^2\sqrt{x}}dx$
      let: $\sqrt{x}=t\;→\frac{1}{2\sqrt{x}}dx=dt$
      $=\int \frac{2}{2\sqrt{x}\sin^2\sqrt{x}}dx=2\int \frac{1}{\sin^2t}dt
      =\frac{2}{\tan t}+C$
    17. ¶$\int \frac{1}{x^2}(1+\frac{1}{x})^2dx$
      let: $1+\frac{1}{x}=t\;→-\frac{1}{x^2}dx=dt$
      $=-\int t't^2dt=-\frac{1}{3}t^3+C$
    18. ¶$\int \frac{(\sqrt{x}+1)^5}{\sqrt{x}}dx$
      let: $\sqrt{x}+1=t\;→\frac{1}{2\sqrt{x}}dx=dt$
      $=2\int t^5dt$
    19. ¶$\int \frac{1}{\tan^2x\sin^2x}dx$
      let: $\frac{1}{\tan x}=t\;→-\frac{1}{\sin^2x}dx=dt$
      $=-\int t^2dt$
    20. ¶$\int \frac{1}{\sqrt{1-\sqrt{x}}}dx$
      let: $\sqrt{1-\sqrt{x}}=t\;→x=(1-t^2)^2\;→dx=2=4t(t^2-1)dt$
      $=4\int \frac{t(t^2-1)}{t}dt=4\int (t^2-1)dt$
    21. ¶$\int_{\sqrt{2}}^{2}\frac{1}{x\sqrt{x^2-1}}dx$
      let: $x=\sec\theta\;→dx=\sec\theta\tan\theta d\theta$
      and: $x:\sqrt{2}→2;,\;\theta:\frac{\pi}{4}→\frac{\pi}{3}$
      from: $1+\tan^2\theta=\sec^2\theta$
      $=\int_{\frac{\pi}{4}}^{\frac{\pi}{3}}\frac{1}{\sec\theta\sqrt{\sec^2\theta-1}}
      \sec\theta\tan\theta dx
      =\int_{\frac{\pi}{4}}^{\frac{\pi}{3}}d\theta=\frac{\pi}{12}$
    22. ¶$\frac{x^2}{(x\sin x+\cos x)^2}dx$
      here: (x\sin x+\cos x)'=\sin x+x\cos x-\sin x=x\cos x
      $=\int \frac{x}{\cos x}\frac{x\cos x}{(x\sin x+\cos x)^2}dx
      =\bigl[-\frac{x}{\cos x}\frac{1}{x\sin x+\cos x}\bigr]
      +\int \frac{\cos x+x\sin x}{\cos^2x}\frac{1}{x\sin x+\cos x}dx$

8. 置換積分法 (微分接触型) (✦):

  • $\int \frac{f'(x)}{f(x)}dx=\ln|f(x)|$
  • $\int (f(x))^af'(x)dx
    =\frac{(f(x))^{a+1}}{a+1},\;(a≠-1)$
  • $f(\sin x)\cos x$
  • $f(\cos x)\sin x$
  • $f(\tan x)\frac{1}{\cos^2x}$
  • $f(\frac{1}{\tan x})\frac{1}{\sin^2x}$
  • Tips-differential:
    • $(\tan x)'=\frac{1}{\cos^2x}$
    • $(\frac{1}{\tan x})'=-\frac{1}{\sin^2x}$
    • $(\frac{1}{x})'=-\frac{1}{x^2}$
    • $(\sqrt{x})'=\frac{1}{2\sqrt{x}}$
    • $(\ln x)'=\frac{1}{x}$
    • $(a^x)'=a^x\ln a$
    • $(a+\sin^2x)'=2\sin x\cos x=\sin 2x$
  • Tips-integral
    • $\int \ln x=x\ln x-x$
    • substitute to:
      $\sqrt{\frac{ax+b}{cx+d}}_n=t$
    • $\frac{1-x}{1+x}=t^2
      \;→x=\frac{1-t^2}{1+t^2}$

>Top 9. Integration by Parts (♥):

  • [by Parts (♥)]
    1. $\int f^0g^0dx=f^0g^{-1}-\int f^1g^{-1}dx$
      $=f^0g^{-1}-\{f^1g^{-2}-\int f^2g^{-2}\}$
      $=f^0g^{-1}-f^1g^{-2}+\int f^2g^{-2}$
      $=f^0g^{-1}-f^1g^{-2}+f^2g^{-3}-f^3g^{-4}+f^4g^{-5}-\cdots±\int$
    2. $\int f^0e^xdx=(f^0-f^1+f^2-f^3+f^4-\cdots)e^x$
    3. $\int f^0e^{-x}dx=-(f^0+f^1+f^2+f^3+f^4+\cdots)e^{-x}$
    4. $\int f^0e^{nx}dx=\bigl(\frac{f^0}{n}-\frac{f^1}{n^2}
      +\frac{f^2}{n^3}-\frac{f^3}{n^4}+\cdots\bigr)e^x$
    5. Cf: $f(x)g(x)=f(x)\cos x$
      $=f^0g^{-1}-f^1g^{-2}+f^2g^{-3}-f^3g^{-4}+f^4g^{-5}$
      $=f^0\sin x-f^1(-\cos x)+f^2(-\sin x)-f^3(\cos x)+f^4(\sin x)-\cdots$
      or, $=f^0g^{-1}+f^1g^1+f^2g^2+f^3g^3+f^4g^4+f^5g^5+\cdots$
      $=f^0g\sin x+f^1\cos x+f^2(-\sin x)+f^3(-\cos x)+f^4(\sin x)+\cdots$
    6. Cf: $f(x)g(x)=f(x)\sin x$
      $=f^0g^{-1}-f^1g^{-2}+f^2g^{-3}-f^3g^{-4}+f^4g^{-5}$
      $=f^0(-cos x)-f^1(-\sin x)+f^2(\cos x)-f^3(\sin x)+f^4(-\cos x)-\cdots$
      or, $=f^0g^{-1}+f^1g^1+f^2g^2+f^3g^3+f^4g^4+f^5g^5+\cdots$
      $=f^0(-\cos x)+f^1(\sin x)+f^2(\cos x)+f^3(-\sin x)+f^4(-\cos x)+\cdots$

  • [Samples]
    1. ¶$\int_{0}^{1}\ln (x^2+1)dx=\int_{0}^{1}(x)'\ln (x^2+1)dx
      =\bigl[x\ln (x^2+1)\bigr]_0^1 -\int_{0}^{1}x･\frac{2x}{x^2+1}dx$
      here: $\int_0^1 \frac{1}{x^2+1}dx=$
      let: $x=\tan\theta\;→dx=\frac{1}{\cos^2\theta}d\theta$
      $=\int_{0}^{\frac{\pi}{4}}\frac{1}{\tan^2\theta+1}\frac{1}{\cos^2}d\theta
      =\int_{0}^{\frac{\pi}{4}}d\theta=\frac{\pi}{4} $
    2. ¶$\int (3x-4)^2(x-2)^5xdx$
      $=(3x-4)^2\frac{1}{6}(x-2)^6-\{(3x-4)\frac{1}{7}(x-2)^7
      -\frac{3}{7}\frac{1}{8}(x-2)^8 \}$
    3. ¶$\int xe^{2x}dx=x\frac{1}{2}e^{2x}-\frac{1}{2}\int e^{2x}dx$
    4. ¶$\int \frac{x}{e^x}dx=x(-e^{-x})-\int (-e^{-x})dx$
    5. ¶$\int x･2^xdx=x\frac{2^x}{\ln 2}-\int \frac{2^x}{\ln 2}$
    6. ¶$\int x\sin xdx=x(-\cos x)-\int (-\cos x)dx$
    7. ¶$\int x^2\cos xdx=x^2\sin x-2x(-\cos x)+2(-\sin x)+C$
    8. ¶$\int x^2\sin\frac{x}{2}dx=x^2(-2\cos\frac{x}{2})
      -\int 2x(-2\cos\frac{x}{2})dx$
      $=x^2(-2\cos\frac{x}{2})+4\{x(2\sin\frac{x}{2})-\int 2\sin\frac{x}{2}\}$
    9. ¶$\int \frac{x}{\cos^2x}dx=x\tan x-\int \tan xdx=x\tan x
      -\int \frac{-(\cos x)'}{\cos x}dx=x\tan x+\ln|\cos x|$
    10. ¶$e^{-x}\sin 2xdx=I=-e^{-x}\sin 2x-\int -e^{-x}2\cos 2xdx$
      $=-e^{-x}\sin 2x+2\{-e^{-x}\cos 2x-\int -e^{-x}(-2\sin 2x)dx\}$
      $=-e^{-x}\sin 2x-2\{e^{-x}\cos 2x-4\int e^{-x}\sin 2xdx\;$ [homotype]
      $→5I=-e^{-x}(\sin 2x+2\cos 2x)$
    11. ¶$\int x^4\sin xdx$
      $=x^4(-\cos x)-4x^3(-\sin x)+12x^2(\cos x)-24x(\sin x)+24(-\cos x)+C$
    12. ¶$\int x^4e^xdx=(x^4-4x^3+12x^2-24x+24)e^x$
    13. ¶$x^32^xdx=x^3\frac{2^x}{\ln 2}-3x^2\frac{2^x}{(\ln 2)^2}
      +6x\frac{2^x}{(\ln 2)^3}-6\frac{2^x}{(\ln 2)^4}+C $
    14. ¶$\int (x^3-2x^2)\cos 2xdx$
      $=(x^3-2x^2)(\frac{1}{2}\sin 2x)-(3x^2-4)(-\frac{1}{4}\cos 2x)$
      $+(6x-4)(-\frac{1}{8}\sin 2x)-(6)(\frac{1}{16}\cos 2x)+C$
    15. ¶$\int (\ln x)^4dx$
      let: $\ln x=t\;→x=e^t\;→dx=e^tdt$
      $=\int t^4e^tdt=(t^4-4t^3+12t^2-24t+24)e^t+C$
    16. ¶$\int \frac{(\ln x)^3}{x^2}dx$
      let: $\ln x=t\;→x=e^t\;→dx=e^tdt$
      $=\int \frac{t^3}{(e^t)^2}e^tdt=\int t^3e^{-t}dt$
      $=-(t^3+3t^2+6t+6)e^{-t}+C$

9. 部分積分法 (♥):

  • >Top Integration by parts: (integral-first!)
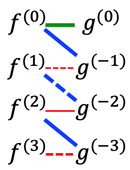
  • integralbyparts.gif
  • $\int f^{(0)}g^{(0)}$
    $ =f^{(0)}g^{(-1)}-f^{(1)}g^{(-2)}$
    $+f^{(2)}g^{(-3)}-f^{(3)}g^{(-4)}$
    $+f^{(4)}g^{(-5)}-f^{(5)}g^{(-6)} ... $
  • Pattern:
    1. $x^m･(ax+b)^n$
    2. $x^m･a^{nx}$
    3. $x^me^{nx}$
    4. $x^m･\sin nx$
    5. $x^m･\cos nx$
    6. $x^m(\ln x)^n$
    7. $e^{mx}\sin nx$
    8. $e^{mx}\cos nx$

  • Tips:
    1. lower order of: $e^{nx},\;a^{nx}$
    2. $(\frac{e^{2x}}{2})'=e^{2x}$
    3. $(a^x)'=a^x\ln a$
    4. $\int \tan x=\int \frac{\sin x}{\cos x}$
      $=-\int \frac{(\cos x)'}{\cos x}
      =-\ln(\cos x)+C$
    5. $\int \cot x=\int \frac{\cos x}{\sin x}$
      $=\int \frac{(\sin x)'}{\sin x}
      =\ln(\sin x)+C$

>Top 10. Integral of product of exponential:

  • [Type of $\int (x-a)^m(x-b)^ndx$]
    1. ¶$\int_a^b(x-a)(x-b)dx=\bigl[\frac{1}{2}(x-a)^2(x-b)\bigr]_a^b
      -\int_{a}^{b}\frac{1}{2}(x-a)^2dx$
      $=-\frac{1}{2}\bigl[\frac{1}{3}(x-a)^3\bigr]_a^b=-\frac{1}{6}(b-a)^3$
    2. $\int_a^b(x-a)^2(x-b)dx=\bigl[\frac{1}{3}(x-a)^3(x-b)\bigr]_a^b
      -\int_a^b\frac{1}{3}(x-a)^3dx$
      $ =-\frac{1}{3}\bigl[\frac{1}{4}(x-a)^4\bigr]_a^b=-\frac{1}{12}(b-a)^4$
    3. $\int_a^b(x-a)^2(x-b)^2dx=\bigl[\frac{1}{3}(x-a)^3(x-b)
      -\frac{1}{3･4}(x-a)^42(x-b)$
      $+\frac{1}{3･4･5}(x-a)^5･2\bigr]_a^b=-\frac{1}{30}(b-a)^5$
    4. $\int_{2}^{3}(2x-6)\sqrt{x-2}=\bigl[(2x-6)\{\frac{2}{3}(x-2)^{\frac{3}{2}}\}
      \bigr]_2^3-\int_{3}^{2}2\frac{2}{3}(x-2)^{\frac{3}{2}}dx$

10. 指数関数の積 (e):
  1. attribute to: $\int (x-a)^ndx
    =\frac{1}{n+1}(x-a)^{n+1}+C$
  2. $\int_{a}^{b}(x-a)(x-b)dx
    =-\frac{1}{6}(b-a)^3$
  3. $\int_{a}^{b}(x-a)^2(x-b)dx
    =-\frac{1}{12}(b-a)^4$
  4. $\int_{a}^{b}(x-a)^2(x-b)^2dx
    =\frac{1}{30}(b-a)^5$

>Top 11. Definite integral with absolute value:

  • Split integration interval:
    1. ¶$\int_{\frac{1}{e}}^{e}|\ln x|dx=\int_{\frac{1}{e}}^{1}(-\ln x)dx
      +\int_{1}^{e}\ln xdx$
      $=\bigl[-x\ln x+x\bigr]_{\frac{1}{e}}^1+\bigl[x\ln x-x\bigr]_1^e$
    2. ¶$\int_{\pi}^{0}|\sqrt{3}\sin x+\cos x|dx$
      $=\int_{\frac{5}{6}\pi}^{0}2\sin(x+\frac{\pi}{6})dx
      +\int_{\pi}^{\frac{5}{6}\pi}\{-2\sin (x+\frac{\pi}{6})dx\}$

11. 絶対値付の定積分 (||):

  • recurrence formula: 漸化式
  • $\ln x=x\ln x-x+C$
  • $a\sin\theta+b\cos\theta
    =A\sin (\theta+\alpha)$
  • $\sin\theta+\sqrt{3}\cos\theta
    ＝2\sin (\theta+\frac{\pi}{3})$

>Top 12. Integral of Fractional function (▼):

  • Make less order of numerator than denomirator:
    1. ¶$\int \frac{2x+3}{4x-1}=\int \frac{\frac{1}{2}(4x-1)+\frac{7}{2}}{4x-1}
      =\int \frac{1}{2}+\frac{7}{2(4x-1)}dx=\frac{1}{2}x+\frac{7}{8}\ln|4x-1|+C$
    2. ¶$\int \frac{x-3}{(x-1)(x-2)}=\int (\frac{2}{x-1}-\frac{1}{x-2})dx$
    3. ¶$\int \frac{1}{x(x+1)(x+2)}dx$
      here: $\frac{1}{x(x+1)(x+2)}=\frac{1}{2}\{\frac{1}{x(x+1)}-\frac{1}{(x+1)(x+2)}\}=\frac{1}{2}\{(\frac{1}{x}-\frac{1}{x+1})-(\frac{1}{x+1}-\frac{1}{x+2})\}$}
      $\int* =\frac{1}{2}\ln|x|-\ln|x+1|+\frac{1}{2}\ln|x+2|+C
      =\frac{1}{2}\ln\frac{|x(x+2)|}{(x+1)^2}+C$

12. 分数関数の積分 (♣):
  • $\frac{1}{ab}=\frac{1}{b-a}
    (\frac{1}{a}-\frac{1}{b})$
  • $\frac{1}{abc}=\frac{1}{c-a}
    (\frac{1}{ab}-\frac{1}{bc})$

>Top 13. Integral using symmetry:

  • Symmetri integral:\cases{a&b\\c&d}
    • $\cases{\int_{-a}^{a}f(x)dx=0\;\text{[odd function]}\\
      \int_{-a}^{a}f(x)dx=2\int_{0}^{a}f(x)dx\;\text{[even function]}}w$

  • Symmetric function:
    • ¶$I=\int_{\frac{\pi}{2}}^{0}\frac{\sin x}{\sin x+\cos x}dx$
      $→\int_{\frac{\pi}{2}}^{0}\frac{\cos x}{\sin x+\cos x}dx$
      add: $→\frac{1}{2}\int_{\frac{\pi}{2}}^{0}dx=\frac{\pi}{4}$
    • ¶$I=\int_{-1}^{1}\frac{1}{2}dx\;→\int_{-1}^{1}\frac{e^x}{e^x+e^{-x}}dx$
      symmery: $→I=\int_{-1}^{1}\frac{e^{-x}}{e^x+e^{-x}}dx$
      add: $\frac{1}{2}\int_{1}^{-1}dx=1$

  • Odd/even function:
    1. ¶$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos x(\sin x-x+1)dx$
      $=\int_{*}^{*}(\cos x\sin x-x\cos x+\cos x)dx=2\bigl[\sin x\bigr]_0^{2\pi}$
    2. ¶$\int_1^{-1}(e^x+e^{-x})dx=2\bigl[e^x-e^{-x}\bigr]_0^1$

13. 対称性による積分 (◐):
  • $f(-x)=-f(x),\;$ [odd function]
    • Eg: $x\cos x,\;\cos x\sin x$
  • $f(-x)=f(x),\;$ [even function]

>Top 14. King Property (♠):

  • $I=\int_{a}^{b}f(x)dx=\int_{a}^{b}f(a+b-x)dx$
    • $→2I=\int_{a}^{b}\{f(x)+f(a+b-x)\}dx$
    1. ¶$I=\int_{2}^{3}\frac{x^2}{x^2+(5-x)^2}dx$
      $→2I=\int_{2}^{3}\{\frac{x^2}{x^2+(5-x)^2}+\frac{(5-x)^2}{x^2}\}dx
      =\int_{2}^{3}dx=1→I=\frac{1}{2}$
    2. ¶$I=\int_{0}^{\pi}\frac{x\sin x}{1+\cos^2x}dx$
      $→2I=\int_{0}^{\pi}\{\frac{x\sin x}{1+\cos^2x}
      +\frac{(\pi-x)\sin x}{1+\cos^2x}\}dx=\pi\int_{0}^{\pi}\frac{\sin x}{1+\cos^2x}dx$
      here let: $\cos x=t\;→-\sin xdx=dt\;→(x:0→\pi);\;(t:1→-1)$
      $=\pi\int_{-1}^1\frac{1}{1+t^2}dt$
      let: $t=\tan\theta→dt=\frac{1}{\cos^2\theta}d\theta,
      \;(t:-1→1);\;(\theta:-\frac{\pi}{4}→\frac{\pi}{4})$
      $=\pi\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}d\theta
      =\frac{\pi^2}{2}→I=\frac{\pi^2}{4}$
    3. ¶$I=\int_2^4\frac{\sqrt{\ln(9-x)}}{\sqrt{\ln(9-x)}+\sqrt{\ln(x+3)}}$
      $=\int_2^4\frac{\sqrt{\ln(x+3)}}{\sqrt{\ln(x+3)}+\sqrt{\ln(9-x)}}$
      $[x\;→2+4-x]\; King property$
      $2I=\int_2^4 1dx=2\;→I=1$

14. キング･プロパティ (♠):
  • transfer: $(x,y)→(X,Y)$
    • $y=Y$
    • $\frac{x+X}{2}=\frac{a+b}{2}$
      $→X=a+b-x$

>Top 15. Recurrsive function (♺):

  • Appear the original integral:
    • ¶$I=\int e^{ax}\sin bxdx$
      $=e^{ax}\frac{1}{b}(-\cos bx)+e^{ax}\frac{a}{b^2}\sin bx-\frac{a^2}{b^2}
      \int e^{ax}\sin bxdx$
      $→\frac{a^2+b^2}{b^2}I=e^{ax}(-\frac{1}{b}\cos bx+\frac{a}{b^2}\sin bx)$
      $I=\frac{1}{a^2+b^2}e^{ax}(a\sin bx-b\cos bx)+C$
    • ¶$I=\int e^{ax}\cos bxdx$
      $=e^{ax}\frac{1}{b}\sin bx+e^{ax}\frac{a}{b^2}\cos bx-\frac{a^2}{b^2}
      \int e^{ax}\cos bxdx$
      $→\frac{a^2+b^2}{b^2}I=e^{ax}(\frac{1}{b}\sin bx+\frac{a}{b^2}\cos bx)$
      $I=\frac{1}{a^2+b^2}e^{ax}(b\sin bx+a\cos bx)+C$
    • ¶$\int xe^x\sin xdx$
      here: $\int e^x\sin xdx=\frac{1}{2}e^x(\sin x-\cos x)+C,\;
      \int e^x\cos xdx=\frac{1}{2}e^x(\sin x+\cos x)+C$
      $ =x\frac{1}{2}e^x(\sin x-\cos x)-\frac{1}{2}\int e^x(\sin x-\cos x)dx$
      $=\frac{1}{2}xe^x(\sin x-\cos x)-\frac{1}{2}\int e^x\sin xdx
      +\frac{1}{2}\int e^x\cos xdx $
      $=\frac{1}{2}xe^x(\sin x-\cos x)-\frac{1}{4}e^x(\sin x-\cos x)
      +\frac{1}{4}e^x(\sin x+\cos x)$
      $=\frac{1}{2}e^x(\sin x-\cos x)+\frac{1}{2}e^x\cos x+C$

15. 再帰関数(♺)::

>Top 16. Recurrence relation (n-1):

  • Difference sequence:
  1. $a_{n+1}=pa_n+q$...(*)
    1. $\alpha=p\alpha+q$...(**) [characteristic eq]$\;→(*)-(**)$
    2. ¶$a_{n+1}=4a_n-3,\; a_1=2$
      $→a_{n+1}-1=4(a_n-1)\;→a_n-1=(a_1-1)4^{n-1}=4^{n-1}$
      $→a_n=4^{n-1}+1$

  2. $a_{n+1}=pa_n+qr^n$ [divided by $r^{n+1}$]
    • ¶$a_{n+1}=3a_n+4･5^n,\;a_1=2$
      $\frac{a_{n+1}}{5^{n+1}}=\frac{3}{5}\frac{a_n}{5^n}+\frac{4}{5}$
      $→(\frac{a_{n+1}}{5^{n+1}-2})=\frac{3}{5}(\frac{a_n}{5^n}-2)$ [by char.eq]
      $→\frac{a_n}{5^n}-2=(a_1)(5)^{n-1}$
      $→\frac{a_n}{5^n}=ー\frac{8}{5}(\frac{3}{5})^{n-1}+2
      =a_n=-8･3^{n-1}+2$

  3. $a_{n+1}=pa_n+f^{(n)}$
    • ¶$a_{n+1}=2a_n+n^2-2n+3,\;a_1=3$...(*)
    • target: $a_{n+1}+\alpha(n+1)^2+\beta(n+1)+\gamma
      =2(a_n+\alpha n^2+\beta n+\gamma)$
      $⇔a_{n+1}=2a_n+\alpha n^2+(-2\alpha+\beta)n+\gamma$...(**)
    • compare (*) & (**): $\alpha=1,\;-2\alpha+\beta=-2,\;\gamma=3$
      $\alpha=1,\;\beta=0,\;\gamma=3$
      $→a_{n+1}+(n+1)^2+3=2(a_n+n^2+3)$
      $a_n=n^2+3=(a_1+1+3)2^{n-1}→a_n=2^{n-1}-n^2-3$

  4. $a_{n+1}=f(n)a_n$
    • ¶$a_{n+1}＝\frac{n+1}{n}a_n,\;a_1=3,\;(n≥2)$
      $a_n=\frac{n}{n-1}a_{n-1}=\frac{n}{n-1}\frac{n-1}{n-2}a_{n-2}
      =\frac{n}{n-1}\frac{n-1}{n-2}\frac{n-2}{n-3}\cdots\frac{2}{1}a_1=na_1=3n$
      $ (n=1)$ is also available.$\;\therefore a_n=3n$

  5. $a_{n+1}=p(a_n)^q$
    • ¶$a_{n+1}=3\sqrt{a_n},\;a_1=27$
    • logarithumic tranform (sequence>0):
      $→\log_3a_{n+1}=\log_3 3a_n^{\frac{1}{2}}=1+\frac{1}{2}\log_3a_n$
      $→\log_3a_{n+1}=\frac{1}{2}\log_3a_n+1
      →\log_3a_{n+1}=\frac{1}{2}(\log_3a_n-2)$
      $→\log_3a_n-2=(\log_3a_1-2)(\frac{1}{2})^{n-1}
      →\log_3a_n=(\frac{1}{2})^{n-1}+2\therefore\;a_n=3^{(\frac{1}{2})^{n-1}+2}$

  6. Recurrence including $S_n$:
    • $a_1=S_1,\;a_{n+1}=S_{n+1}-S_n$
    • ¶$S_n=4a_n-6,\;$ when $n=1→a_1=4a_1-6→a_1=2$
      $→a_{n+1}=S_{n+1}-S_n=4a_{n+1}-6(n+1)-4a_n+6n=4a_{n+1}-4a_n-6$
      $→a_{n+1}=\frac{4}{3}a_n+2$
      $a_{n+1}+6=\frac{4}{3}(a_n+6)\; [\alpha=\frac{4}{3}\alpha+2]$
      $→a_n+6=(a_1+6)(\frac{4}{3})^{n-1}=8(\frac{4}{3})^{n-1}$
      $\therefore\;a_n=8(\frac{4}{3})^{n-1}-6$

  7. $a_{n+2}+pa_{n+1}+qa_n=0$
    • $→\alpha^2+p\alpha+q=0$
      $→\cases{a_{n+2}-\alpha_1a_{n+1}=\alpha_2(a_{n+1}-\alpha_1a_n)
      \\a_{n+2}-\alpha_2a_{n+1}=\alpha_1(a_{n+1}-\alpha_2a_n)}$
      $⇔a_{n+2}-(\alpha_1+\alpha_2)a_{n+1}+\alpha_1\alpha_2 a_n$
    • ¶$a_{n+2}-5a_{n;1}+6a_n=0,\;a_1=4,\;a_2=1$
      • $\alpha^2-5\alpha+6=0→(\alpha-2)(\alpha-3)=0→\alpha=2,\;3$
        $\cases{a_{n+2}-2a_{n+1}=3(a_{n+1}-2a_n)...(*)
        \\a_{n+2}-3a_{n+1}=2(a_{n+1}-3a_n)...(**)}$
      • from (*):$a_{n+1}-2a_n=(a_2-2a_1)3^{n-1}=-7･3^{n-1}$
      • from (**):$a_{n+1}-3a_n=(a_2-3a_1)2^{n-1}=-11･2^{n-1}$
      • $a_n=-7･3^{n-1}+11･2^{n-1}$
    • ¶$a_{n+2}-6a_{n+1}+9a_n=0→a_1=1,\;a_2=5$
      $→a_{n+2}-3a_{n+1}=3(a_{n+1}-3a_n),\;[\alpha=3]$
      $a_{n+1}-3a_n=(a_2-3a_1)3^{n-1}=2･3^{n-1}$
      $→a_{n+1}=3a_n+\frac{2}{3}3^n
      →\frac{a_{n+1}}{3^{n+1}}=\frac{a_n}{3^n}＋\frac{2}{9}$
      $\frac{a_n}{3^n}=\frac{a_1}{3}+(n-1)\frac{2}{9}$
      $\therefore\;a_n=3^{n-2}(2n+1)$
  • $I_n=\int \sin^nxdx,\;(n=0,1,2,\cdots)$
    • $I_n=-\frac{1}{n}\sin^{n-1}x\cos x+\frac{n-1}{n}I_{n-2},\;(n=2,3,4,\cdots)$
    • Proof: $I_n=\int \sin^{n-1}\sin xdx$
      let: $f=\sin^{n-1}x\;→f'=(n-1)\sin^{n-2}x\cos x,\;g=-\cos x\;→g'=\sin x$
      $I_n=\sin^{n-1}x(-\cos x)-\int (n-1)\sin^{n-2}x\cos x(-\cos x)dx$
      $=\sin^{n-1}x(-\cos x)+(n-1)\int \sin^{n-2}x(1-\sin^2x)dx$
      $→I_n=-\sin^{n-1}x\cos x+(n-1)I_{n-2}-(n-1)I_n$
      $→nI_n=-\sin^{n-1}x\cos x+(n-1)I_{n-2}$
      $\therefore\;I_n=-\frac{1}{n}\sin^{n-1}x\cos x+\frac{n-1}{n}I_{n-2}$

  • $I_n=\int \cos^nxdx,\;(n=0,1,2,\cdots)$
    • $I_n=\frac{1}{n}\cos^{n-1}x\sin x+\frac{n-1}{n}I_{n-2},\;(n=2,3,4,\cdots)$
    • Proof: $I_n=\int \cos^{n-1}\cos xdx$
      let: $f=\cos^{n-1}x\;→f'=(n-1)\cos^{n-2}x(-\sin x),\;g=\sin x\;→g'=\cos x$
      $I_n=\cos^{n-1}x\sin x-\int (n-1)\cos^{n-2}x(-\sin x)\sin xdx$
      $=\cos^{n-1}x\sin x+(n-1)\int \cos^{n-2}x(1-\cos^2x)dx$
      $→I_n=\cos^{n-1}x\sin x+(n-1)I_{n-2}-(n-1)I_n$
      $→nI_n=\cos^{n-1}x\sin x+(n-1)I_{n-2}$
      $\therefore\;I_n=\frac{1}{n}\cos^{n-1}x\sin x+\frac{n-1}{n}I_{n-2}$

  • $I_n=\tan^ndx,\;(n=0,1,2,\cdots)$
    • $I_n=\frac{1}{n-1}\tan^{n-1}x-I_{n-2},\;(n=2,3,4,\cdots)$
    • Proof: $In=\int \tan^{n-2}\tan^2xdx=\int \tan^{n-2}(\frac{1}{\cos^2x}-1)dx$
      $=\int \bigl(\frac{\tan^{n-2}x}{\cos^2x}-\tan^{n-2}\bigr)dx
      =\int \frac{\tan^{n-2}x}{\cos^2x}dx-I_{n-2}$
      let: $t=\tan x\;→dt=\frac{1}{\cos^2x}dx$
      here: $\int \frac{\tan^{n-2}x}{\cos^2x}dx=\int t^{n-2}dt=\frac{t^{n-1}}{n-1}+C
      =\frac{\tan^{n-1}x}{n-1}+C$
      $\therefore\;I_n=\frac{1}{n-1}\tan^{n-1}x-I_{n-2}$

  • $I_n=\int (\ln x)^ndx,\;(n=0,1,2,\cdots)$
    • $I_n=x(\ln x)^n-nI_{n-1},\;(n=1,2,3,\cdots)$
    • Proof: let: $f=(\ln x)^n\;→f'=n(\ln x)^{n-1}\frac{1}{x};\;g=x\;→g'=1$
      $\int (\ln x)^ndx=(\ln x)^nx-\int n()^{n-1}\frac{1}{x}xdx
      =x(\ln x)^n-n\int (\ln x)^{n-1}dx$
      $\therefore\;I_n=x(\ln x)^n-nI_{n-1}$

  • $I_n=\int x^ne^xdx,\;(n=1,2,3,\cdots)$
    • $I_n=x^ne^x-nI_{n-1}$
    • Proof: $I_n=x^ne^x-\int nx^{n-1}e^xdx=x-ne^x-nI_{n-1}$

  • $I_n=\int \frac{x^n}{e^x}dx,\;(n=1,2,3,\cdots)$
    • $I_n=-\frac{x^n}{e^x}-nI_{n-1}$
    • Proof: $I_n=\int x^ne^{-1}=x^n(-e^{-x})-\int nx^{n-1}(-e^{-x})
      =-x^ne^{-x}+nI_{n-1}$

  • $I_n=\int \frac{e^x}{x^n}dx,\;(n=1,2,3,\cdots)$
    • $I_n=-\frac{e^x}{(n-1)x^{n-1}}+\frac{1}{n-1}I_{n-1}$
    • Proof: $I_n=\int e^xx^{-n}
      =e^x\frac{1}{-n+1}x^{-n+1}-\int e^x\frac{1}{-n+1}x^{-n+1}dx
      =\frac{-e^x}{(n-1)x^{n-1}}+\frac{1}{n-1}I_{n-1}$

  • $I_n=\int x^m(\ln x)^ndx,\;(n=1,2,3,\cdots)$
    • $I_n=\frac{x^{m+1}(\ln x)^n}{m+1}-\frac{n}{m+1}I_{n-1}$
    • Proof: $\int (\ln x)^nx^mdx
      =(\ln x)^n\frac{1}{m+1}x^{m+1}
      -\int n(\ln x)^{n-1}\frac{1}{x}\frac{1}{m+1}x^{m+1}
      =\frac{x^{m+1}(\ln x)^n}{m+1}-\frac{n}{m+1}I_{n-1} $

  • $I_n=\int x^n\sin xdx,\;(n=2,3,4,\cdots)$
    • $I_n=-x^n\cos x+nx^{n-1}\sin x-n(n-1)I_{n-2}$
    • Proof; from: $\int f^0g^0=f^0g^{-1}-f^1g^{-2}+\int f^2g^{-2}$
      let: $f^0=x^n,\;g^0=\sin x$
    • $I_n=x^n(-\cos x)-nx^{n-1}(-\sin x)+\int n(n-1)x^{n-2}(-\sin x)dx$
      $=-x^n\cos x+nx^{n-1}\sin x-n(n-1)\int x^{n-2}\sin xdx$
      $\therefore\; I_n=-x^n\cos x+nx^{n-1}\sin x-n(n-1)I_{n-2}$

16. 漸化式 (n-1):

  • arithmetic sequence: 等差型
  • geometric sequence: 等比型
  • difference sequence: 階差型
  1. $a_{n+1}=a_n+d$
  2. $a_{n+1}=ra_n$
  3. $a_{n+1}=a_n+f(n)$
  4. $a_{n+1}=pa_n+q$
  5. $a_{n+1}=pa_n+q･r^n$
  6. $a_{n+1}=pa_n+f(n)$
  7. $a_{n+1}=f(n)a_n$
  8. $a_{n+1}=p(a_n)^q$
  9. $a_{n+1}=pa_n$
  10. $S_n$ included
  11. $a_{n+2}+pa_{n+1}+qa_n=0$

>Top 17. Parametric variable (✔):

  • Parameter:
    1. ¶$\int \frac{1}{\sqrt{1-x^2}}dx$
      from: $x^2+y^2=1$
      let: $x=\sin t\;→dx=\cos tdt$
      $=\int \frac{1}{\cos t}\cos tdt=\int dt$

    2. ¶$\int \frac{1}{\sqrt{1+x^2}}dx$
      from:
      let: $x=\frac{1}{2}(e^t-e^{-t})\;(=\sinh t)$ [hyperbolic]
      $→dx=\frac{1}{2}(e^t+e^{-t})dt\;→e^t=x+\sqrt{x^2+1}→t=\ln (x+\sqrt{x^2+1})$
      $=\int \frac{1}{\sqrt{1+\frac{(e^t+e^{-t})^2}{4}}}\frac{et+e^{-t}}{2}dt
      =\int \frac{1}{\frac{e^t+e^{-t}}{2}}\frac{e^t+e^{-t}}{2}dt=\int dt
      =\ln (x+\sqrt{x^2+1})+C $

    3. Parameter:
      • $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$
      • $\frac{d^2y}{dx^2}=\frac{d}{dx}(\frac{dy}{dx})
        =\frac{d}{dt}(\frac{dy}{dx})\frac{dt}{dx}$
    4. [Sample]
      • ¶$\cases{x=t-\sin t\\y=1-\cos t}$

17. 媒介変数 (✔):

>Top 18. Beta function (Euler integral of the first kind (β)):

  • $\int_{b}^{a}(x-a)^m(x-b)^ndx=\frac{(-1)^nm!n!}{(m+n+1)!}(b-a)^{m+n+1}$
    $=\bigl[\frac{1}{m+1}(x-a)^{m+1}(x-b)^n\bigr]_a^b
    -\int \frac{n}{m+1}(x-a)^{m+1}(x-b)^{n-1}dx$
    $=\frac{(-1)^nm!n!}{(m+n-1)!}\int_{b}^{a}\frac{(x-a)^{m+n}}{m+n}dx$
    here coefficient: $\frac{n}{m+1}\frac{n-1}{m+2}\cdots\frac{2}{m+n-1}
    =\frac{m!n!}{(m+n-1)!}$
    • $m=1, n=1:\;→\int_{b}^{a}(x-a)(x-b)dx=-\frac{1}{6}(b-a)^3$
    • $m=2, n=1:\;→\int_{b}^{a}(x-a)^2(x-b)dx=-\frac{1}{12}(b-a)^4$
    • $m=2, n=2:\;→\int_{b}^{a}(x-a)^2(x-b)^2dx=\frac{1}{30}(b-a)^5$

18. ベータ関数 (β):
  • eulerintegral.gif

>Top 19. Gaussian integral:

  • Gaussian integral:
  • $I=\int_{-\infty}^{\infty}e^{-x^2}dx$
    • $I^2=\bigl(\int_{-\infty}^{\infty}e^{-x^2}dx\bigr)
      \bigl(\int_{-\infty}^{\infty}e^{-y^2}dy\bigr)$
      $=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}dxdy$
    • let: $x=r\cos\theta,\;y=r\sin\theta$
      $\;→I^2=\int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2)}rdrd\theta
      =\int_{0}^{2\pi}d\theta\int_{0}^{\infty}re^{-r^2}dr$
      $=2\pi\bigl[-\frac{1}{2}e^{-r^2}\bigr]_0^{\infty}=\pi$
      $I=\sqrt{\pi},\;[I>0]$
  • ¶1: $\int_{-\infty}^{\infty}e^{-ax^2}dx,\;(a>0)$
    • let: $y=\sqrt{a}x,\;dy=\sqrt{a}dx$
      $=\int_{-\infty}^{\infty}e^{-y^2}\frac{1}{\sqrt{a}}dy=\sqrt{\frac{\pi}{a}}$
  • ¶2: $\int_0^{\infty}e^{-ax^2}dx,\;(a>0)$
    • $=\frac{1}{2}\sqrt{\frac{\pi}{a}}\;$[even function]
  • ¶3: $\int_{0}^{\infty}xe^{-ax^2}dx,\;(a>0)$
    $=\bigl[-\frac{1}{2a}e^{-ax^2}\bigr]_0^{\infty}=\frac{1}{2a}\;$ [odd function]
  • ¶4: G=$\int_{-\infty}^{\infty}x^2e^{-ax^2}dx,\;(a>0)$
    $I(a)=\int_{-\infty}^{\infty}e^{-ax^2}dx$
    $→\frac{d(a)}{da}=\int_{-\infty}^{\infty}\frac{\partial }{\partial a}(e^{-ax^2})dx$
    $=\int_{-\infty}^{\infty}x^2e^{-ax^2}dx$
    $\therefore\;G=-\frac{dI(a)}{da}=\frac{d}{da}(\pi^{\frac{1}{2}}a^{-\frac{1}{2}})
    ＝\frac{1}{2a}\sqrt{\frac{\pi}{a}}$
  • ¶5: $\int_0^{\infty}x^3e^{-ax^2}dx,\;(a>0)$
    $=\int_0^{\infty}x^2xe^{-ax^2}dx=\bigl[x^2(-\frac{1}{2}e^{-ax^2})\bigr]_0^{\infty}
    - \int_0^{\infty}2x(-\frac{1}{2}e^{-ax^2})dx
    =\frac{1}{a}\int_0^{\infty}xe^{-ax^2}dx=\frac{1}{2a^2}\;$ [←¶3]
  • ¶6: $\int_{-\infty}^{\infty}x^4e^{-ax^2}dx,\;(a>0)$
    $=\frac{d^2}{da^2}(\pi^{\frac{1}{2}}a^{-\frac{1}{2}})
    =\frac{3}{4a^2}\sqrt{\frac{\pi}{a}}$
  • ¶7: [general form]
    $\cases{\int_{0}^{\infty}x^{2n+1}e^{-ax^2}dx=\frac{n!}{2a^{n+1}}
    \\\int_{-\infty}^{\infty}x^{2n}e^{-ax^2}dx
    =\frac{(2n-1)!!}{2^na^n}\sqrt{\frac{\pi}{a}}}$
  • ¶8: $\int_{-\infty}^{\infty}e^{-ax^2+b+c}dx,\;(a>0)$
    $=\int_{-\infty}^{\infty}e^{-a(x-\frac{b}{2a})^2+\frac{b^2}{4a}+c}dx
    =e^{\frac{b^2}{4a}+c}\int_{-\infty}^{\infty}e^{-a(x-\frac{b}{2a})}\;$
    [parallel displacement]
    $=\sqrt{\frac{\pi}{a}}e^{\frac{b^2}{4a}+c}$

19. ガウス積分 (G):

  • $\cases{x=r\cos\theta
    \\y=\sin\theta}$
  • Jacobian:
    $\pmatrix{\frac{\partial x}{\partial r}
    &\frac{\partial x}{\partial\theta}
    \\\frac{\partial y}{\partial r}
    &\frac{\partial y}{\partial\theta}} =\pmatrix{\cos\theta&-r\sin\theta
    \\\sin\theta&r\cos\theta}$

>Top 20. l'Hôpital's rule (Ô):

  • Average-Value theorem:
    • If $f(x)$ is continuous over the interval $[a,b]$ then:
      $^\exists c\in(a,b)\;\text{such that}\; f(c)
      =\frac{1}{b-a}\int_{a}^{b}f(x)dx\;$[average, or mean value: there exists a point $c$ such that $f(c)$ equals to the averge of $f(x)$]

  • l'Hôpital's rule (or Bernoulli's rule):
    • Let $L$ be an open interval containing $c$ (for two-sided limit or one-sided limit if $c$ is infinite).
    • the real valued function $f,\;g$ are asumed continuous and differentiable on an open interval $I$ except at $c$, and additionally $g'(x)≠0$ on $I$ except at $c$.
    • if it is assumed that $\;lim_{x\to c}\frac{f'(x)}{g'(x)}=L$;
      this rule is applied to the ratio of $L$ if it has a finite or infinite limit, but not to the ratio fluctuating permanently.
      • If either $\displaystyle\lim_{x\to c}f(x)=\lim_{x\to c}g(x)=0\;$$ [\frac{0}{0}]$
        , or $\;\;\;\displaystyle\lim_{x\to c}|f(x)|=\lim_{x\to c}|g(x)|=\infty$,
        then $\;\displaystyle\lim_{x\to c}\frac{f(x)}{g(x)}=L\;$$ [\frac{\infty}{\infty}]$

  • Sample:
    1. ¶$\frac{x+\sin x}{x}$, where $c=±\infty$, then,
      • $\frac{f'(x)}{g'(x)}=\frac{1+\cos x}{1}\;[\cos x$ oscillates]
      • But the origianl function can be:
        $\lim_{x\to\infty}\frac{f(x)}{g(x)}
        =\lim_{x\to\infty}\bigl(1+\frac{\sin x}{x}\bigr)=1$
    2. ¶$\lim_{x\to 0}\frac{e^x-1}{x^2+x}$
      $=\lim_{x\to 0}\frac{\frac{d}{dx}(e^x-1)}{\frac{d}{dx}(x^2+x)}
      =\lim_{x\to 0}\frac{e^x}{2x+1}=1$
    3. ¶$\lim_{x\to\infty}\frac{x^n}{e^x}$
      $ =\lim_{x\to\infty}\frac{nx^{n-1}}{e^x}
      =n\lim_{x\to\infty}\frac{x^{n-1}}{e^x}\cdots $
      when l'Hôpital's rule repeats, the exponent will be zero: thus the limit will be zero.
    4. ¶$\lim_{x\to 0}\frac{e^x-e^{-1}}{x}=\lim_{x\to 0}\frac{e^x+e^{-1}}{1}=2$
    5. ¶$\lim_{x\to\infty}\frac{x^2}{e^{2x}}=\lim_{x\to\infty}\frac{2x}{2e^{2x}}
      =\lim_{x\to\infty}\frac{2}{4e^{2x}}=0$
    6. ¶$\lim_{x\to +0}x^2\ln x=\lim_{x\to +0}\frac{\ln x}{\frac{1}{x^2}}
      =\lim_{x\to +0}\frac{\frac{1}{x}}{-\frac{2}{x^3}}
      =\lim_{x\to +0}(-\frac{1}{2}x^2)=0$

20. ロピタルの定理 (Ô):

  • set difference: 差集合 \
  • extented real number: 拡大実数
  • one-sidede limit: 片側極限
  • $c, L$ を拡大実数であり、
    以下条件が満たされるとする。
    $\displaystyle\lim_{x\to c}f(x)
    =\lim_{x\to c}g(x)=0$
    $\displaystyle\lim_{x\to c}f(x)
    =\pm\lim_{x\to c}g(x)=\pm\infty$
  • ある開区間から$c$を除いた点で
    $g'(x)≠0$
  • ここで$\displaystyle\lim_{x\to c}
    \frac{f'(x)}{g'(x)}=L$
    が存在すれば
  • $\displaystyle\lim_{x\to c}
    \frac{f(x)}{g(x)}=L$である。
    なお、片側極限でもよい。

  • $\displaystyle\lim_{x\to\infty}
    \frac{a^x}{x^r}=\infty$
  • $\displaystyle\lim_{x\to\infty}
    \frac{x^r}{\ln x}=\infty$

>Top 21. Last boss integral:

  • 100th question of the interal by Yobinori:
    1. ¶$ I=\int_{0}^{\frac{\pi}{4}}\sqrt{\tan x}dx$
      • let $t=\sqrt{\tan x}$→ $t^2=\tan x$→$2tdt=\frac{1}{\cos^2x}dx$
        →$dx=2t\cos^2xdt=\frac{2t}{1+\tan^2x}dt=\frac{2t}{1+t^4}dt$
      • integral range: $x:0→\frac{\pi}{4};\; t:0→1$
      • $I=\int_{0}^{1}\frac{2t^2}{1+t^4}dt$
      • where, $t^4+1=(t^2+1)^2-2t=(t^2+\sqrt{2}+1)(t^2-\sqrt{2}+1)=P$
      • where, $\frac{2t^2}{P}=\frac{At+B}{t^2+\sqrt{2}t+1}
        +\frac{Ct+D}{(t^2-\sqrt{2}t+1)}$
        →$A=-\frac{1}{\sqrt{2}}; B=0; C=\frac{1}{\sqrt{2}}; D=0$
      • thus, $I=\frac{1}{\sqrt{2}}\{\int_{0}^{1}\frac{t}{t^2-\sqrt{2}t+1}dt
        -\int_{0}^{1}\frac{t}{t^2+\sqrt{2}t+1}dt\}
        =\frac{1}{\sqrt{2}}\{I_1-I_2\}$
      • where, $I_1=\frac{1}{2}\{\int_{0}^{1}\frac{(t^2-\sqrt{2}t+1)'
        +\sqrt{2}}{t^2-\sqrt{2}t+1}dt\}
        =\frac{1}{2}\{\int_{0}^{1}\frac{(t^2-\sqrt{2}t+1)'}{t^2-\sqrt{2}t+1}dt
        +\int_{0}^{1}\frac{\sqrt{2}}{t^2-\sqrt{2}t+1}dt\}$
        • where, $\frac{\sqrt{2}}{t^2-\sqrt{2}t+1}
          =\frac{\sqrt{2}}{(t-\frac{1}{\sqrt{2}})^2+\frac{1}{2}}$
        • let, $t-\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\tan\theta\;→dt
          =\frac{1}{\sqrt{2}}\frac{1}{\cos^2\theta}d\theta$
          $t: 0→1;\;\theta: -\frac{\pi}{4}→\alpha$ such that $\;\tan\alpha
          =\sqrt{2}-1\;(0<\alpha<\frac{\pi}{2})$
        • $I_1=\frac{1}{2}\bigl\{\bigl[\ln |t^2-\sqrt{2}t+1|\bigr]_0^1
          +2\int_{-\frac{\pi}{4}}^{\alpha}\frac{\sqrt{2}}{\tan^2\theta+1}
          \frac{1}{\sqrt{2}\cos^2\theta}d\theta\bigr\}\\
          =\frac{1}{2}\bigl\{\ln (2-\sqrt{2})+2\int_{-\frac{\pi}{4}}^
          {\alpha}d\theta\bigr\}
          =\frac{1}{2}\ln(2-\sqrt{2})+\alpha+\frac{\pi}{4}$
      • where, $I_2=\frac{1}{2}\{\int_{0}^{1}\frac{(t^2+\sqrt{2}t+1)'
        -\sqrt{2}}{t^2+\sqrt{2}t+1}dt\}
        =\frac{1}{2}\{\int_{0}^{1}\frac{(t^2+\sqrt{2}t+1)'}{t^2+\sqrt{2}t+1}dt
        -\int_{0}^{1}\frac{\sqrt{2}}{t^2+\sqrt{2}t+1}dt\}$
        • $I_2= \frac{1}{2}\bigl\{\bigl[\ln |t^2+\sqrt{2}t
          +1|\bigr]_0^1-2\int_{\frac{\pi}{4}}^{\beta}\theta\bigl\}
          =\frac{1}{2}\ln (2+\sqrt{2})-\beta+\frac{\pi}{4}$
        • where, $\beta$ is such that $\;\tan\beta=\sqrt{2}+1\;(0<\beta<\frac{\pi}{2})$
      • thus, $I=\frac{1}{\sqrt{2}}(\frac{1}{2}\ln \frac{2-\sqrt{2}}
        {2+\sqrt{2}}+\alpha+\beta)$
        • where, $\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}
          {1-\tan\alpha\tan\beta}=\frac{2\sqrt{2}}{1-1}=\infty$
        • $→\alpha+\beta=\frac{\pi}{2}$
      • then, $I=\frac{1}{\sqrt{2}}\bigl(\frac{1}{2}\ln \frac{2-\sqrt{2}}{2+\sqrt{2}}
        +\alpha+\beta\bigr)=\frac{1}{\sqrt{2}}
        \{\ln (\sqrt{2}-1)+\frac{\pi}{2}\}$
        • where, $\frac{2-\sqrt{2}}{2+\sqrt{2}}=\frac{6-2\sqrt{2}}{2};\;3-2\sqrt{2}=(\sqrt{2}-1)^2$

21. ラスボス積分:

  1. Tips:
    • ルートを外す:
      $\sqrt{\tan x}=t$と置く。
      定積分の範囲; dx→dt計算
    • ４乗の因数分解:
      $(t^4+1)=(t^2+1)^2-2t$
    • 部分分数分解:
    • $\tan x$への置換:
      $\frac{1}{x^2+a^2}$のパターンは
      $x=a\tan\theta$と置く
    • 長い式は
      $I=I_1+I=2$
      $I_1=I_{11}+I_{12}$と分割計算
    • 定積分の範囲変換:
      確定値が出ない場合はsuch that方式:
      $\alpha$ such that $\;\tan\alpha=$
      遠く。→後の期待
    • 三角関数の公式:
      $\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}
      {1-\tan\alpha\tan\beta}$
    • $\frac{\pi}{2}$で$\tan\theta→\infty$
    • 微分接触型関数の積分:
      $\int f^af'dx=\frac{f^{a+1}}{a+1}+C$
    • 二重根号の外し方:
      $\sqrt{a+b\pm 2\sqrt{ab}}=\sqrt{a}\pm \sqrt{b}$

>Top 22. xxxx:

22. xxxx:
Comment
  • In some high schools, there seems a hobby club named 'integral solution club'; I would have participated such a club if it had existed such a club in my old high school.
  • Solution of integrals resembles a kind of game, which is useful in activating one's aging brain during staying home.
  • 一部の高校には'積分クラブ'があるらしい。もしかつての私の高校にそのようなクラブがあれば、きっと参加したのに。
  • 積分の解法は一種のゲームに似ている。それは自宅で引きこもりの老頭の活性化に役立つ。

| Top | Home | Article | Bookshelf | Keyword | Author | Oxymoron |